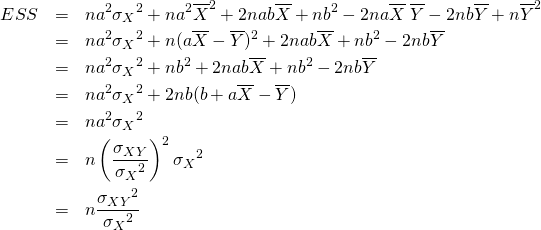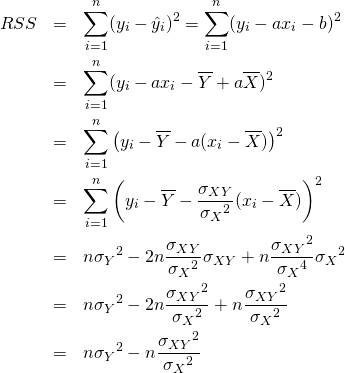リテラル
要素をリテラルで指定する。
2次元配列は行列形式できれいに表示されるが、3次元以上は1行表示になる。
|
1 2 3 4 5 6 7 8 9 10 11 |
print(np.array([0, 1, 2])) # [0 1 2] print(np.array([[0, 1, 2], [0, 2, 4], [0, 3, 6]])) # [[0 1 2] # [0 2 4] # [0 3 6]] print([[[0, 1], [2, 3]], [[1, 2], [3, 4]], [[2, 3], [4, 5]], [[3, 4], [5, 6]], [[4, 5], [6, 7]], [[5, 6], [7, 8]]]) # [[[0, 1], [2, 3]], [[1, 2], [3, 4]], [[2, 3], [4, 5]], [[3, 4], [5, 6]], [[4, 5], [6, 7]], [[5, 6], [7, 8]]] |
リストでもタプルでも結果は同じ。
|
1 2 3 4 5 |
print(np.array([0, 1, 2, 3])) print(np.array((0, 1, 2, 3))) # [0 1 2 3] # [0 1 2 3] |
自動生成
配列形状を指定して全要素を特定の値で埋める
全要素が0、1の配列
numpy.zeros(shape, [dtype=None], [order='C'])
numpy.ones(shape, [dtype=None], [order='C'])
引数はどちらも同じで、配列形状、データタイプ、行列優先の指定。
多次元配列を生成する場合、配列のサイズをタプルとして引数に渡す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
print(np.zeros(3)) # [0. 0. 0.] print(np.zeros((2, 3))) # [[0. 0. 0.] # [0. 0. 0.]] print(np.ones(3)) # [1. 1. 1.] print(np.ones((2, 3))) # [[1. 1. 1.] # [1. 1. 1.]] |
全要素の数値を指定
numpy.full(shape, fill_value, [dtype=None], [order='C'])]
|
1 2 3 4 5 6 |
print(np.full(5, -1)) # [-1 -1 -1 -1 -1] print(np.full((2, 3), np.exp(1))) # [[2.71828183 2.71828183 2.71828183] # [2.71828183 2.71828183 2.71828183]] |
他の配列と同じ形状で特定の値を埋める
全要素が0、1の配列
numpy.zeros_like(a, [dtype=None], [order='C'])
numpy.ones_like(a, [dtype=None], [order='C'])
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
a = np.array([0, 1, 2]) print(np.zeros_like(a)) print(np.ones_like(a)) # [0 0 0] # [1 1 1] b = np.array([[0, 1, 2], [3, 4, 5]]) print(np.zeros_like(b)) print(np.ones_like(b)) # [[0 0 0] # [0 0 0]] # [[1 1 1] # [1 1 1]] |
全要素の値を指定
numpy.full_like(a, fill_value, [dtype=None], [order='C'])]
|
1 2 3 4 5 6 |
print(np.full_like(a, -1)) print(np.full_like(b, -2)) # [-1 -1 -1] # [[-2 -2 -2] # [-2 -2 -2]] |
初期化せず配列枠だけ確保する
zeros()、ones()と同じで、配列の形だけを確保するが各要素は初期化しない。
この場合も多次元配列ではサイズのタプルを引数で渡す。
|
1 2 3 4 5 6 |
print(np.empty(3)) # [6.90878481e-305 6.92648110e-305 6.48616890e-317] print(np.empty((2, 3))) # [[7.79018398e-075 2.23185784e-074 1.41890730e-075] # [9.39249846e-076 3.97945113e-315 0.00000000e+000]] |
配列形状を(1, 1)で指定すると、1要素の2次元配列が確保される。
|
1 2 |
print(np.empty((1, 1))) # [[2.]] |
配列形状を数値0で指定すると、空の配列が確保される。
|
1 2 3 4 5 6 7 8 9 10 |
a = np.empty(0) print(a) a = np.append(a, 1) print(a) a = np.append(a, 2) print(a) # [] # [1.] # [1. 2.] |
配列形状で0の次元が含まれると空の配列になる。
|
1 2 3 4 5 |
print(np.empty((0, 3, 2))) # [] print(np.empty((3, 0, 2))) # [] |
内包表記
リストの内包表記が使える。
|
1 2 3 |
print(np.array([x for x in range(0, 5)])) # [0 1 2 3 4] |
range()関数
普通にrange()関数も使える。
|
1 2 3 |
print(np.array(range(5)) # [0 1 2 3 4] |
numpy.arange()~間隔を指定
numpy.arrange([start=0], stop, [step=1], [dtype=None])
numpy.arange()関数はrange()関数よりも高速な生成が可能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
start = time.time() for n in range(1000): a = np.arange(10000) lap = time.time() - start print('arange: {0} sec'.format(lap)) for n in range(1000): a = np.array(range(10000)) end = time.time() - start print('range : {0} sec'.format(end - lap)) # arange: 0.003025054931640625 sec # range : 1.2017848491668701 sec |
range()関数と同じようにパラメータを設定。dtypeはデータ型を指定。
|
1 2 3 4 5 6 7 8 9 |
print(np.arange(10)) print(np.arange(1, 10)) print(np.arange(1, 10, step=2)) print(np.arange(1, 10, step=2, dtype=float)) # [0 1 2 3 4 5 6 7 8 9] # [1 2 3 4 5 6 7 8 9] # [1 3 5 7 9] # [1. 3. 5. 7. 9.] |
range()関数は整数しか引数に指定できないが、numpy.arange()関数はfloatの指定が可能。
|
1 2 3 4 5 |
print(np.arange(5.0)) print(np.arange(0, 5, step=0.5)) # [0. 1. 2. 3. 4.] # [0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5] |
numpy.linspace()~分割数を指定
numpy.linspace(start, stop, [num=50], [endpoint=True], [retstep=False], [dtype=None])
初期値と終了値を指定して、その間を等分割したリストを返す。分割数を指定しないとデフォルトで50分割。基本の型はfloat。
|
1 2 3 4 5 6 7 8 9 10 11 |
print(np.linspace(0, 5)) # [0. 0.10204082 0.20408163 0.30612245 0.40816327 0.51020408 # 0.6122449 0.71428571 0.81632653 0.91836735 1.02040816 1.12244898 # 1.2244898 1.32653061 1.42857143 1.53061224 1.63265306 1.73469388 # 1.83673469 1.93877551 2.04081633 2.14285714 2.24489796 2.34693878 # 2.44897959 2.55102041 2.65306122 2.75510204 2.85714286 2.95918367 # 3.06122449 3.16326531 3.26530612 3.36734694 3.46938776 3.57142857 # 3.67346939 3.7755102 3.87755102 3.97959184 4.08163265 4.18367347 # 4.28571429 4.3877551 4.48979592 4.59183673 4.69387755 4.79591837 # 4.89795918 5. ] |
この分割数は区間数ではなく、生成される数列の個数である点に注意。以下の例では0~1の間で10個の数値を生成させるため、区間数は9となる(植木算の考え方)。
|
1 2 3 4 |
print(np.linspace(0, 1, num=10)) # [0. 0.11111111 0.22222222 0.33333333 0.44444444 0.55555556 # 0.66666667 0.77777778 0.88888889 1. ] |
デフォルトでは終端値を含めるが、含めないようにもできる。
|
1 2 3 |
print(np.linspace(0, 1, num=10, endpoint=False)) # [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9] |
生成された数列と分割幅のタプルを返すことができる。
|
1 2 3 4 5 6 7 8 |
a = np.linspace(0, 9, num=10, retstep=True) print(a) print(a[0]) print(a[1]) # (array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.]), 1.0) # [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] # 1.0 |
特定の行列の生成
numpy.identity()~単位行列
numpy.identity(n)
正方行列の1辺の要素数を指定して、単位行列を生成する。
|
1 2 3 4 5 |
print(np.identity(3)) # [[1. 0. 0.] # [0. 1. 0.] # [0. 0. 1.]] |
numpy.tri()~下三角行列の生成
numpy.tri(n)
左下の要素が1の下三角行列を生成する。
|
1 2 3 4 5 6 |
print(np.tri(4)) # [[1. 0. 0. 0.] # [1. 1. 0. 0.] # [1. 1. 1. 0.] # [1. 1. 1. 1.]] |
numpy.tril()、numpy.triu()~行列の三角化
numpy.tril(matrix)
nunmpy.triu(matrix)
与えられた行列を下三角/上三角化。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
m = np.reshape(np.arange(16), (4, 4)) print(m) print(np.tril(m)) print(np.triu(m)) # [[ 0 1 2 3] # [ 4 5 6 7] # [ 8 9 10 11] # [12 13 14 15]] # [[ 0 0 0 0] # [ 4 5 0 0] # [ 8 9 10 0] # [12 13 14 15]] # [[ 0 1 2 3] # [ 0 5 6 7] # [ 0 0 10 11] # [ 0 0 0 15]] |
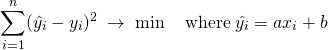
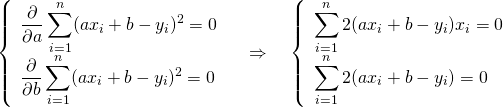
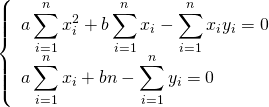
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} a \\ b \end{array} \right] = \left[ \begin{array}{c} \dfrac{n S_{xy} - S_x S_y}{n S_{xx} - {S_x}^2} \\ \dfrac{S_{xx} S_y - S_x S_{xy}}{n S_{xx} - {S_x}^2} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-5ab9943a0ccf9c81304d639401e154d8_l3.png)