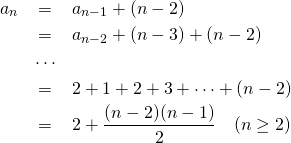基本死活の基本。隅にかかる辺の四子～六子並び。
四子は、先手でも生きていない。
五子の場合は、先手なら生き、後手だと死。
六子の場合は後手でも生き。まず、外から狭めてきた場合。
中に打ち込んできた場合。
辺の六子～八子並び。
六子は先手でも生きない。
七子は先手だと生き。
七子で後手だと生きない。
八子は後手でも生き。まず外から狭めてきた場合。
中に打ち込んできた場合。
隅の曲がり四目は、日本棋院囲碁規約(平成元年四月)の第七条-2において「死」とされている。
| 第九条の「対局の停止」後での、死活確認の際における同一の劫での取り返しは、行うことができない。ただし劫を取られた方が取り返す劫のそれぞれにつき着手放棄を行った後は、新たにその劫を取ることができる。 |
単独三々入りの場合、入った方は外側からの一手に手を抜くことができる。
ハネた側から入り込んできた場合。
2の一へのオキ(1)。
2の一へのオキ(2)。
2の二へのオキ。
逆側からハネてきても生き。
中手の手数を知っておくと、詰碁などで役に立つ。
たとえば次のケースでは白のダメが8つあいている。五目中手の手数が8手と知っていれば、黒から右の一団を五目中手の形にして攻め合いに勝てることがわかる。
目数とその一団を殺すまでの手数の対応は以下の通り。
| 一目 | 1 |
| 二目 | 2 |
| 三目 | 3 |
| 四目(三菱／団子) | 5 |
| 五目(中手／花五) | 8 |
| 六目中手 | 12 |
これは当たり前。
これも当たり前。ただし1手目を打ち込まれた石を抜くとその後すぐに死となるので、付き合わない前提。
これは1手打ち込んだ後、次の手の交換で二目になるので、1手＋二目の2手で3手。
四目で殺せるのは団子と三菱の二通り。どちらの場合も四目は2手打った後の交換で三目になるので、2手＋三目の3手で5手。
五目中手を詰めていって四目になるまでに3手。そこから四目の手数は5手だから、五目中手を殺す手数は3手＋5手で8手。
六目中手を詰めていって五目になるまでに4手。そこから五目の手数は8手だから、六目中手を殺す手数は4手＋8手で12手。
ある目数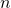
から相手が連続して詰めていって、取られる前に詰められた石を抜くと目数が
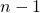になる。
目数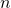の時の手数を
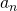とすると、取られる前の交換はカウントしないので、以下の漸化式が得られる。
(1) 
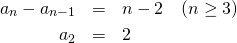
(2) 
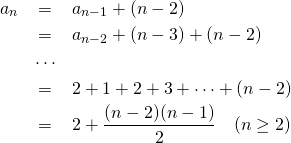
漸化式の定義時は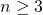
の条件だったが、
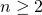でも成り立ち、冒頭の表の6目中手まで整合していることが確認できる。
中手が問題になるのは6目以下であり、現実的には手数を2, 3, 5, 8, 12と覚えておけばよく、この計算はあくまで趣味の範囲。
一間バサミから三々に入った後、三つ伸びずにハネるのはよくない。
上手が様子を見るのに敢えてハネる場合、サガリに対して以下の進行が最善で、三々に入った白よし。
小ゲイマカカリに対して一間バサミから三々に入られたとき、かかった石と入った石を分断して外勢を張る定石。
三々に入られた側が分断して外勢を張りながら先手を取れる。
黒が伸びずにハネた場合の定石はずれはこちら
たとえば黒△の援軍があるところに白Aとカカリ、黒Bのハサミに白Cと三々に飛び込んだ時。
この場合は三々に入られて閉じ込めた方が後手になるので、向かい側に友軍がいる方がよい。
白が鉄柱にせずに突き出してきたときは、切った石を捨て石にして外勢を張る。切る順が逆になると白が好形になる。
白が鉄柱にせず下がったとき。
単独で三々に入った場合、布石によって厚みが期待できるなら押さえる方向を選択。外勢を張るが後手になる。
入った方が生きてから先手で他へ回る。
デギリは無理。「グルグルマワシ」が痛快。
黒が伸びずに二段にハネる定石で、外勢を張りながら先手を取る方法と、後手になるが外勢と実利をある程度とる方法がある。
先手で外勢を張りたいときの打ち方。
外勢と実利の両方を取りたい場合。後手になる。
二段バネに対して反対側をハネて、守らずに切ってくるケース。
その後の影響が大きい、と折角切った石が無駄になる場合。
切られた後に這った場合。まず伸びる手。
這いに対して単に切る手。
より確実に咎める場合。
守らずにダメを詰めて来たら、外勢を張る。
白は抜け出ることができる。
| 西暦 | 和暦 | 日本 | 外国 |
| 1333 | 後醍醐天皇の皇子、護良親王が征夷大将軍となる | ||
| 1334 | 後醍醐天皇による建武の新政～延喜・天暦の治 | ||
| 1335 | 07月、中先代の乱～足利尊氏が北条時之を滅ぼす 12月、箱根・竹ノ下の戦い～足利尊氏が新田義貞を破る／以降、延元の乱 |
||
| 1336 | 01月、足利尊氏入京、後醍醐天皇は比叡山へ | ||
| 1336 | 02月、豊島河原合戦～足利尊氏vs新田義貞・北畠顕家→尊氏が九州へ敗走 05月、湊川の戦い～足利尊氏・直義vs新田義貞・楠正成→尊氏が勝利 06月、足利尊氏が入京 08月、光明天皇が即位(北朝) 11月、尊氏が御成敗式目を定める 12月、後醍醐天皇は吉野へ(南朝) 以後、南北朝時代へ |
||
| 1338 | 05月、石津の戦い～北畠顕家(南朝)vs高師直(北朝)→北朝の勝利 07月、藤島の戦い～新田義貞(南朝)vs斯波高経(北朝)→北朝の勝利 08月、足利尊氏が征夷大将軍となる |
||
| 1342 | 天龍寺船が元(モンゴル)に渡航・貿易 | ||
| 1348 | 四条畷の戦い～楠正行(南朝)vs高師直(北朝)→北朝の勝利 | ||
| 1349 | 鎌倉府設置～初代長官(鎌倉公方)は足利基氏／補佐役として関東管領が置かれ、主に上杉一族が世襲 | ||
| 1350 | 観応の擾乱～足利政権の内乱～1352まで | ||
| 1352 | 守護が年貢の半分を徴発可能とし、以後、守護大名へと発展 | ||
| 1358 | 足利尊氏死去 | ||
| 1359 | 12月、足利義詮が第2代将軍となる | ||
| 1368 | 足利義満が第3代将軍となる | ||
| 1370 | この頃までに「太平記」がまとめられる 前期倭寇の時代 |
||
| 1378 | 足利義満が京都室町通に花の御所を造営 | ||
| 1379 | 天授5/康暦1 | 康暦の政変～室町幕府管領の細川頼之が失脚 | |
| 1392 | 明徳3/元中9 | 閏10.5(JD11.19)明徳の和約～南北朝の合一／南朝の後亀山天皇が吉野から京都に帰還し、北朝の後小松天皇に三種の神器を譲って退位 | |
| 1394 | 足利義満が太政大臣となる | ||
| 1397 | 足利義満が北山に金閣寺(鹿苑寺)を建立 | ||
| 1401 | 明との国交の開始～民からの国書では足利義満が日本国王 | ||
| 1404 | 勘合貿易の開始 | ||
| 1419 | 応永の外寇～李氏朝鮮による対馬侵攻 | ||
| 1428 | 正長1 | 8月～9月、正長の土一揆～農民による初の一揆・私徳政 | |
| 1429 | 正長2 | 2月、播磨の国一揆～政治的要求 3.15、足利義教が第6代将軍に～石清水八幡宮での籤引き・万人恐怖 尚巴志が三山統一により琉球王国を建国 |
|
| 1432 | 上杉憲実が足利学校を再興 | ||
| 1435 | 比叡山延暦寺の変 | ||
| 1441 | 6.24、嘉吉の乱～赤松満祐が足利義教を暗殺 嘉吉の土一揆~徳政令 |
||
| 1443 | 足利義政が8代目将軍となる～正室は日野富子 | ||
| 1455 | 享徳3 | 12.27(1.15AD)、享徳の乱～鎌倉公方と関東管領の内乱 | |
| 1457 | 康生3/長禄1 | コシャマインの戦い～和人に対するアイヌの武装蜂起 | |
| 1466 | 文正1 | 9.6、文正の政変～足利義政は側近を失い将軍権力は衰退→応仁の乱へ | |
| 1467 | 応仁1 | 応仁の乱～端緒は1.18(2.22AD)の御霊合戦 | |
| 1477 | 文明9 | 応仁の乱の終結～幕府による「天下静謐」の祝宴→戦国時代へ | |
| 1485 | 文明17 | 山城国一揆～国人・農民による8年間の自治 | |
| 1487 | 長享1 | 長享の乱～山内・扇谷両上杉家の戦い～太田道灌暗殺と北条早雲の躍進 | |