matplotlib.pyplot – グラフ

2019-10-29 / tau / コメントする

グラフの描画

pyplot

figure, axes

グラフの種類

3次元グラフ

3次元グラフの概要

tips

matplotlib.pyplot – 基本的なグラフの描画方法

2019-10-29 / tau / コメントする

概要

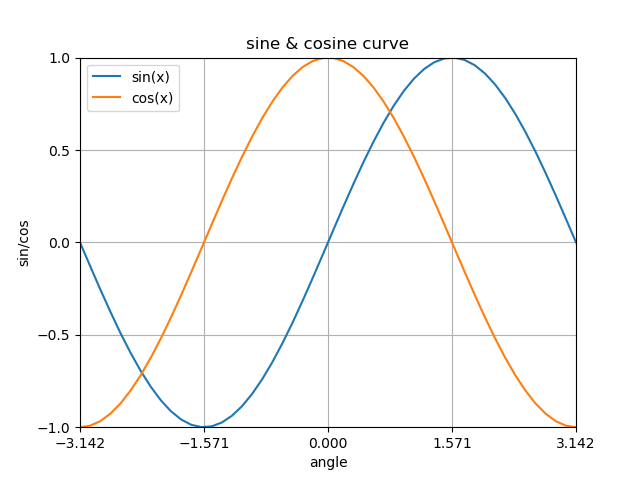
pyplotのみを使った基本的なグラフの描画方法。一般的にはmatplotlib.pyplotをpltというエイリアスでインポートする。

この例では、pyplotの関数のみを用いて1つのグラフに2つの曲線を描画し、タイトルや軸ラベル、凡例などを追加している。

また、軸目盛の間隔を設定したり、グリッドを描かせたりしている。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi, endpoint=True)
y1 = np.sin(x)
y2 = np.cos(x)

plt.title("sine & cosine curve")
plt.xlabel("angle")
plt.ylabel("sin/cos")

plt.xlim(-np.pi, np.pi)
plt.ylim(-1, 1)

plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
plt.yticks(np.linspace(-1, 1, num=5, endpoint=True))

plt.grid(True)

plt.plot(x, y1, label="sin(x)")
plt.plot(x, y2, label="cos(x)")

plt.legend(loc="upper left")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi, endpoint=True)

y1 = np.sin(x)

y2 = np.cos(x)

plt.title("sine & cosine curve")

plt.xlabel("angle")

plt.ylabel("sin/cos")

plt.xlim(-np.pi, np.pi)

plt.ylim(-1, 1)

plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])

plt.yticks(np.linspace(-1, 1, num=5, endpoint=True))

plt.grid(True)

plt.plot(x, y1, label="sin(x)")

plt.plot(x, y2, label="cos(x)")

plt.legend(loc="upper left")

plt.show()

実行結果は以下の通り。

ライブラリーのインポート

import numpy as np
import matplotlib.pyplot as plt

1 2	import numpy as np import matplotlib.pyplot as plt

グラフ描画のためのパッケージ、matplotlob.pyplotをpltとしてインポートしている。また、関数描画のためにnumpyもnpとしてインポート。

描画する関数

x = np.linspace(-np.pi, np.pi, endpoint=True)
y1 = np.sin(x)
y2 = np.cos(x)

x = np.linspace(-np.pi, np.pi, endpoint=True)

y1 = np.sin(x)

y2 = np.cos(x)

ここではpyplotのplot()で描画するため、2つの三角関数を準備している。

xの値は共通で、numpy.linspace()で−π～+πの間で等間隔にデフォルトの50個の点を準備。endpoint=Trueで終端の点も含めている。

そのxの値に対して、sin、cosの関数の値をy1、y2に保存。numpy.linspace()から得られるxや、それに対してNumpyのユニバーサル関数で計算されるy1、y2はndarray。

各種設定

タイトルと軸ラベル

plt.title("sine & cosine curve")
plt.xlabel("angle")
plt.ylabel("sin/cos")

plt.title("sine & cosine curve")

plt.xlabel("angle")

plt.ylabel("sin/cos")

pyplot.title()の引数でグラフのタイトル、pyplot.xlabel()とpyplot.ylabel()の引数でx軸とy軸のラベルを設定している。

軸の範囲

plt.xlim(-np.pi, np.pi)
plt.ylim(-1, 1)

1 2	plt.xlim(-np.pi, np.pi) plt.ylim(-1, 1)

pyplot.xlim()とpyplot.ylim()で、それぞれの軸の下限値と上限値を設定している。x軸については−π～+πとしている。

軸目盛

plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
plt.yticks(np.linspace(-1, 1, num=5, endpoint=True))

1 2	plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi]) plt.yticks(np.linspace(-1, 1, num=5, endpoint=True))

pyplot.xticks()、pyplot.yticks()の引数で、軸目盛に表示する値を設定している。引数は、表示させたい軸の値をリストとして与える。

x軸については−π、−π/2、0、π/2、πの値を直接与え、y軸についてはnumpy.linspace()関数で、-1～+1の間で等間隔な5点(-1、-0.5、0、0.5、1)を計算している。

グリッド(補助線)

plt.grid(True)

1	plt.grid(True)

グラフの描画エリア内に、軸目盛に対応した細い補助線を描くため、pyplot.grid()の引数をTrueで指定している。

グラフの描画

plt.plot(x, y1, label="sin(x)")
plt.plot(x, y2, label="cos(x)")

1 2	plt.plot(x, y1, label="sin(x)") plt.plot(x, y2, label="cos(x)")

pyplot.plot()の引数にxとy1及びy2を指定してグラフを描いている。2つのplot()関数を書くことで、関数は重なって描かれる。

それぞれのグラフに対してlabel引数を指定していて、それらは凡例表示に使われる。

凡例の表示

plt.legend(loc="upper left")

1	plt.legend(loc="upper left")

pyplot.legend()で凡例を設定している。

凡例にはpyplot.plot()で指定したラベルが使われるため、pyplot.legend()はpyplot.plot()の後に書かなければならない。

また、凡例の表示位置をloc引数で指定していて、この場合は左上に凡例が表示される。凡例の位置は、upper/lowerとleft/rightをスペースで繋いだ文字列で指定。

グラフの表示

plt.show()

1	plt.show()

pyplot.show()でグラフを表示させている。

Python3 – pandas

2019-10-28 / tau / コメントする

概要

pandasはPythonのライブラリで、Rのdata frameのようなデータフレームをDataFrameクラスとして提供している。

その由来はpanel-data-sらしいが、公式ドキュメントにはそういう記述は見当たらない。

DataFrame

pandas.DataFrame

2019-10-28 / tau / コメントする

情報・内容の取得

データの概観

DataFrameの規模・サイズ、列ごとの概要や基本的な統計量などを確認する方法

基本的なパラメーターの取得

DataFrameの行数・列数・サイズや、列名・行名、データ内容の配列を取得する方法

DataFrameの生成

要素の操作

at/iat（単独要素）、loc/iloc（単独要素・スライス）による参照・変更

列の操作

DataFrameでの直接列名指定、locでのスライスを含む指定などによる列の参照・追加・更新・削除（assign、insert含む）

行の操作

DataFrameで直接行を指定して参照

DataFrameで直接行番号を指定する場合はスライスで指定する。1行取り出す場合でもdf[col:col+1]のようにスライスにしなければならない。

maskによる行の抽出

DataFrameの特定列に対する条件式は、その条件に応じたTrue/Falseを要素とするSeriesオブジェクトを返す。

そのSeriesオブジェクトをDataFrameの引数とすると、Trueに対応する行だけが抽出される。

names = ["Austin", "Bill", "Charie", "Dick"]
ages = np.array([38, 25, 52, 18])
data_frame = pd.DataFrame({'name': names, 'age': ages})
print("source data frame:\n{}".format(data_frame))
mask = data_frame['age'] > 30
print("mask data frame:\n{}".format(mask))
print("masked data frame:\n{}".format(data_frame[mask]))

# source data frame:
#      name  age
# 0  Austin   38
# 1    Bill   25
# 2  Charie   52
# 3    Dick   18
# mask data frame:
# 0     True
# 1    False
# 2     True
# 3    False
# Name: age, dtype: bool
# masked data frame:
#      name  age
# 0  Austin   38
# 2  Charie   52

names = ["Austin", "Bill", "Charie", "Dick"]

ages = np.array([38, 25, 52, 18])

data_frame = pd.DataFrame({'name': names, 'age': ages})

print("source data frame:\n{}".format(data_frame))

mask = data_frame['age'] > 30

print("mask data frame:\n{}".format(mask))

print("masked data frame:\n{}".format(data_frame[mask]))

# source data frame:

# name age

# 0 Austin 38

# 1 Bill 25

# 2 Charie 52

# 3 Dick 18

# mask data frame:

# 0 True

# 1 False

# 2 True

# 3 False

# Name: age, dtype: bool

# masked data frame:

# name age

# 0 Austin 38

# 2 Charie 52

これをまとめて次のようにも書ける。

print(data_frame[data_frame['age'] > 30])

#      name  age
# 0  Austin   38
# 2  Charie   52

print(data_frame[data_frame['age'] > 30])

# name age

# 0 Austin 38

# 2 Charie 52

抽出結果の特定の列を参照可能。結果はSeriesオブジェクト。

print(data_frame[data_frame['age'] > 30]['name'])

# 0    Austin
# 2    Charie
# Name: name, dtype: object

print(data_frame[data_frame['age'] > 30]['name'])

# 0 Austin

# 2 Charie

# Name: name, dtype: object

queryによる行の抽出

DataFrameのquery()メソッドでも行を抽出できる。

print(data_frame)
print(data_frame.query('age > 30'))

#      name  age
# 0  Austin   38
# 1    Bill   25
# 2  Charie   52
# 3    Dick   18
#      name  age
# 0  Austin   38
# 2  Charie   52

print(data_frame)

print(data_frame.query('age > 30'))

# name age

# 0 Austin 38

# 1 Bill 25

# 2 Charie 52

# 3 Dick 18

# name age

# 0 Austin 38

# 2 Charie 52

抽出結果から特定の列を参照可能。結果はSeriesオブジェクト。

print(data_frame.query('age > 30')['name'])

# 0    Austin
# 2    Charie
# Name: name, dtype: object

print(data_frame.query('age > 30')['name'])

# 0 Austin

# 2 Charie

# Name: name, dtype: object

行の追加

1行追加する場合

1行追加する場合、locで新たな行インデックスを指定して内容を与える。

import numpy as np
from pandas import DataFrame

source = np.array([
    ["zero", 0],
    ["one", 1],
    ["two", 2]
])
df = DataFrame(source, columns=['number', 'numeric'])
print(df)
#   number numeric
# 0   zero       0
# 1    one       1
# 2    two       2

df.loc[3] = ["three", 3]
print(df)
#   number numeric
# 0   zero       0
# 1    one       1
# 2    two       2
# 3  three       3

import numpy as np

from pandas import DataFrame

source = np.array([

["zero", 0],

["one", 1],

["two", 2]

])

df = DataFrame(source, columns=['number', 'numeric'])

print(df)

# number numeric

# 0 zero 0

# 1 one 1

# 2 two 2

df.loc[3] = ["three", 3]

print(df)

# number numeric

# 0 zero 0

# 1 one 1

# 2 two 2

# 3 three 3

複数行追加する場合

複数行（＝配列）を追加する場合、その配列をDataFrameオブジェクトとしてからappend()メソッドを使う。ただし単純に追加すると、新たな行・列として拡張されてしまう。

source = np.array([
    ["zero", 0],
    ["one", 1],
    ["two", 2]
])

df = DataFrame(source, columns=['number', 'numeric'])
print(df)

to_add = np.array([
    ["three", 3],
    ["four", 4]
])

df_to_add = DataFrame(to_add)
print(df.append(df_to_add))

#   number numeric      0    1
# 0   zero       0    NaN  NaN
# 1    one       1    NaN  NaN
# 2    two       2    NaN  NaN
# 0    NaN     NaN  three    3
# 1    NaN     NaN   four    4

source = np.array([

["zero", 0],

["one", 1],

["two", 2]

])

df = DataFrame(source, columns=['number', 'numeric'])

print(df)

to_add = np.array([

["three", 3],

["four", 4]

])

df_to_add = DataFrame(to_add)

print(df.append(df_to_add))

# number numeric 0 1

# 0 zero 0 NaN NaN

# 1 one 1 NaN NaN

# 2 two 2 NaN NaN

# 0 NaN NaN three 3

# 1 NaN NaN four 4

これを回避するためには、追加する行の列名をcolumnsで明示する。ただしこの段階では、追加された行のインデックスが連続していない。

df_to_add = DataFrame(to_add, columns=['number', 'numeric'])
print(df.append(df_to_add))

#   number numeric
# 0   zero       0
# 1    one       1
# 2    two       2
# 0  three       3
# 1   four       4

df_to_add = DataFrame(to_add, columns=['number', 'numeric'])

print(df.append(df_to_add))

# number numeric

# 0 zero 0

# 1 one 1

# 2 two 2

# 0 three 3

# 1 four 4

インデックスを連続させるためには、ignore_index=Trueを指定する。

df_new = df.append(df_to_add, ignore_index=True)
print(df_new)

#   number numeric
# 0   zero       0
# 1    one       1
# 2    two       2
# 3  three       3
# 4   four       4

df_new = df.append(df_to_add, ignore_index=True)

print(df_new)

# number numeric

# 0 zero 0

# 1 one 1

# 2 two 2

# 3 three 3

# 4 four 4

DataFrameの結合

cocatメソッド～縦方向の結合

concat()メソッドは複数のDataFrameを縦に結合した結果を返す。列の構成が同じDataFrameオブジェクトをリスト化して与える。

import pandas as pd

df1 = pd.DataFrame([[10, 11, 12], [20, 21, 22]])
df2 = pd.DataFrame([[30, 31, 32], [40, 41, 42]])

df = pd.concat([df1, df2])
print(df)

#     0   1   2
# 0  10  11  12
# 1  20  21  22
# 0  30  31  32
# 1  40  41  42

import pandas as pd

df1 = pd.DataFrame([[10, 11, 12], [20, 21, 22]])

df2 = pd.DataFrame([[30, 31, 32], [40, 41, 42]])

df = pd.concat([df1, df2])

print(df)

# 0 1 2

# 0 10 11 12

# 1 20 21 22

# 0 30 31 32

# 1 40 41 42

列数が異なるDataFrameを結合すると、余った要素にはNaNがセットされる。

import pandas as pd

df1 = pd.DataFrame([[10, 11], [20, 21]])
df2 = pd.DataFrame([[30, 31, 32], [40, 41, 42]])

df = pd.concat([df1, df2])
print(df)

#     0   1     2
# 0  10  11   NaN
# 1  20  21   NaN
# 0  30  31  32.0
# 1  40  41  42.0

import pandas as pd

df1 = pd.DataFrame([[10, 11], [20, 21]])

df2 = pd.DataFrame([[30, 31, 32], [40, 41, 42]])

df = pd.concat([df1, df2])

print(df)

# 0 1 2

# 0 10 11 NaN

# 1 20 21 NaN

# 0 30 31 32.0

# 1 40 41 42.0

joinメソッド～横方向の結合

join()メソッドは元のDataFrameに引数のDataFrameを結合した結果を返す。結合は行のインデックスに着目して実行され、インデックスが同じデータは同じ行の列方向に追加される。すなわち、同じ行数で異なる列のDataFrameを結合するのに適している。

破壊的な処理ではなく、元のDataFrameはそのままで新しいDataFrameが生成される。

import pandas as pd

data1 = [
    [1, 4],
    [2, 5],
    [3, 6]
]

data2 = [
    [7, 10],
    [8, 11],
    [9, 12]
]

df1 = pd.DataFrame(data1, columns=['1', '2'])
df2 = pd.DataFrame(data2, columns=['3', '4'])

print(df1)
#    1  2
# 0  1  4
# 1  2  5
# 2  3  6

print(df2)
#    3   4
# 0  7  10
# 1  8  11
# 2  9  12

print(df1.join(df2))
#    1  2  3   4
# 0  1  4  7  10
# 1  2  5  8  11
# 2  3  6  9  12

import pandas as pd

data1 = [

[1, 4],

[2, 5],

[3, 6]

]

data2 = [

[7, 10],

[8, 11],

[9, 12]

]

df1 = pd.DataFrame(data1, columns=['1', '2'])

df2 = pd.DataFrame(data2, columns=['3', '4'])

print(df1)

# 1 2

# 0 1 4

# 1 2 5

# 2 3 6

print(df2)

# 3 4

# 0 7 10

# 1 8 11

# 2 9 12

print(df1.join(df2))

# 1 2 3 4

# 0 1 4 7 10

# 1 2 5 8 11

# 2 3 6 9 12

この例では2つのDataFrameの行が一致しており、列が異なるので、横方向に結合されている。同じ列名が存在する場合はValueErrorとなる。

3つ以上のDataFrameを結合したい場合（引数に2つ以上のDataFrameを指定したい場合）は、それら複数のDataFrameをタプルかリストでまとめて指定する。

data3 = [[13], [14], [15]]

df3 = pd.DataFrame(data3, columns=['5'])

print(df3)
#     5
# 0  13
# 1  14
# 2  15

print(df1.join([df2, df3]))
#    1  2  3   4   5
# 0  1  4  7  10  13
# 1  2  5  8  11  14
# 2  3  6  9  12  15

data3 = [[13], [14], [15]]

df3 = pd.DataFrame(data3, columns=['5'])

print(df3)

# 5

# 0 13

# 1 14

# 2 15

print(df1.join([df2, df3]))

# 1 2 3 4 5

# 0 1 4 7 10 13

# 1 2 5 8 11 14

# 2 3 6 9 12 15

合計の計算と合計欄

以下の配列を使う。

import numpy as np
import pandas as pd

df = pd.DataFrame(np.arange(9).reshape(3, 3))
print(df)

#    0  1  2
# 0  0  1  2
# 1  3  4  5
# 2  6  7  8

import numpy as np

import pandas as pd

df = pd.DataFrame(np.arange(9).reshape(3, 3))

print(df)

# 0 1 2

# 0 0 1 2

# 1 3 4 5

# 2 6 7 8

sum()メソッドはSeriesオブジェクトを返す。

sums_in_col = df.sum()
sums_in_row = df.sum(axis=1)

print("sums in column")
print(sums_in_col)

print("sums in row")
print(sums_in_row)

# sums in column
# 0     9
# 1    12
# 2    15
# dtype: int64
# sums in row
# 0     3
# 1    12
# 2    21
# dtype: int64

sums_in_col = df.sum()

sums_in_row = df.sum(axis=1)

print("sums in column")

print(sums_in_col)

print("sums in row")

print(sums_in_row)

# sums in column

# 0 9

# 1 12

# 2 15

# dtype: int64

# sums in row

# 0 3

# 1 12

# 2 21

# dtype: int64

合計欄としてDataFrameに追加する場合、行／列いずれかの合計を計算して追加し、その上で他方の合計を計算して追加すると、総計まで計算できる。

行の追加はlocプロパティーを通じて、列の追加は列名を指定して行う。

sums_in_col = df.sum()
df.loc['Total'] = sums_in_col
print(df)
#        0   1   2
# 0      0   1   2
# 1      3   4   5
# 2      6   7   8
# Total  9  12  15

sums_in_row = df.sum(axis=1)
df['Total'] = sums_in_row
print(df)

#        0   1   2  Total
# 0      0   1   2      3
# 1      3   4   5     12
# 2      6   7   8     21
# Total  9  12  15     36

sums_in_col = df.sum()

df.loc['Total'] = sums_in_col

print(df)

# 0 1 2

# 0 0 1 2

# 1 3 4 5

# 2 6 7 8

# Total 9 12 15

sums_in_row = df.sum(axis=1)

df['Total'] = sums_in_row

print(df)

# 0 1 2 Total

# 0 0 1 2 3

# 1 3 4 5 12

# 2 6 7 8 21

# Total 9 12 15 36

より詳しい合計や率の算出方法はこちら。

ソート

sums_in_col = df.sum()
sums_in_row = df.sum(axis=1)

print("sums in column")
print(sums_in_col)

print("sums in row")
print(sums_in_row)

# sums in column
# 0     9
# 1    12
# 2    15
# dtype: int64
# sums in row
# 0     3
# 1    12
# 2    21
# dtype: int64

sums_in_col = df.sum()

sums_in_row = df.sum(axis=1)

print("sums in column")

print(sums_in_col)

print("sums in row")

print(sums_in_row)

# sums in column

# 0 9

# 1 12

# 2 15

# dtype: int64

# sums in row

# 0 3

# 1 12

# 2 21

# dtype: int64

以下のデータを使用

import numpy as np
from pandas import DataFrame

lst = np.array([
    ["Alex", "DC", 44, 168],
    ["Bert", "NY", 18, 176],
    ["Carl", "CA", 26, 175],
    ["Daryl", "DC", 32, 182],
    ["Eddy", "CA", 58, 192]
])

df = DataFrame(lst, columns=["name", "state", "age", "height"])
print(df)

#     name state age height
# 0   Alex    DC  44    168
# 1   Bert    NY  18    176
# 2   Carl    CA  26    175
# 3  Daryl    DC  32    182
# 4   Eddy    CA  58    192

import numpy as np

from pandas import DataFrame

lst = np.array([

["Alex", "DC", 44, 168],

["Bert", "NY", 18, 176],

["Carl", "CA", 26, 175],

["Daryl", "DC", 32, 182],

["Eddy", "CA", 58, 192]

])

df = DataFrame(lst, columns=["name", "state", "age", "height"])

print(df)

# name state age height

# 0 Alex DC 44 168

# 1 Bert NY 18 176

# 2 Carl CA 26 175

# 3 Daryl DC 32 182

# 4 Eddy CA 58 192

`sort_values()`～列名を指定してソート

デフォルトは昇順。元のオブジェクトは変更されず、ソート後のDataFrameオブジェクトが生成されて返される。

df_sort_age = df.sort_values("age")
print(df_sort_age)

#     name state age height
# 1   Bert    NY  18    176
# 2   Carl    CA  26    175
# 3  Daryl    DC  32    182
# 0   Alex    DC  44    168
# 4   Eddy    CA  58    192

df_sort_age = df.sort_values("age")

print(df_sort_age)

# name state age height

# 1 Bert NY 18 176

# 2 Carl CA 26 175

# 3 Daryl DC 32 182

# 0 Alex DC 44 168

# 4 Eddy CA 58 192

`ascending`パラメーター

ascending=Falseを指定すると降順でソート。

print(df.sort_values("age", ascending=False))

#     name state age height
# 4   Eddy    CA  58    192
# 0   Alex    DC  44    168
# 3  Daryl    DC  32    182
# 2   Carl    CA  26    175
# 1   Bert    NY  18    176

print(df.sort_values("age", ascending=False))

# name state age height

# 4 Eddy CA 58 192

# 0 Alex DC 44 168

# 3 Daryl DC 32 182

# 2 Carl CA 26 175

# 1 Bert NY 18 176

`reset_index()`～インデックスの降り直し

ソート後にインデックスを振りなおす場合、reset_index()メソッドを使う。このメソッドも元のオブジェクトを変更しない。

print(df_sort_age.reset_index())

   index   name state age height
# 0      1   Bert    NY  18    176
# 1      2   Carl    CA  26    175
# 2      3  Daryl    DC  32    182
# 3      0   Alex    DC  44    168
# 4      4   Eddy    CA  58    192

print(df_sort_age.reset_index())

index name state age height

# 0 1 Bert NY 18 176

# 1 2 Carl CA 26 175

# 2 3 Daryl DC 32 182

# 3 0 Alex DC 44 168

# 4 4 Eddy CA 58 192

降りなおした後のインデックスで元のインデックスを上書きする場合は、drop=Trueを指定。

print(df_sort_age.reset_index(drop=True))

#     name state age height
# 0   Bert    NY  18    176
# 1   Carl    CA  26    175
# 2  Daryl    DC  32    182
# 3   Alex    DC  44    168
# 4   Eddy    CA  58    192

print(df_sort_age.reset_index(drop=True))

# name state age height

# 0 Bert NY 18 176

# 1 Carl CA 26 175

# 2 Daryl DC 32 182

# 3 Alex DC 44 168

# 4 Eddy CA 58 192

複数列によるソート

複数列を指定してソートする場合、ソートの優先順にリストで指定。ascendingパラメーターに同じ要素数のTrue/Falseリストを与えて、列ごとの昇順／降順を指定可能。

print(df.sort_values(["state", "height"], ascending=[True, False]))

#     name state age height
# 4   Eddy    CA  58    192
# 2   Carl    CA  26    175
# 3  Daryl    DC  32    182
# 0   Alex    DC  44    168
# 1   Bert    NY  18    176

print(df.sort_values(["state", "height"], ascending=[True, False]))

# name state age height

# 4 Eddy CA 58 192

# 2 Carl CA 26 175

# 3 Daryl DC 32 182

# 0 Alex DC 44 168

# 1 Bert NY 18 176

axisの方向

各種演算・処理の引数でaxisを設定するときの、行方向・列方向がまぎらわしいので整理。

DataFrameの設定

列のインデックス設定

set_index()メソッドにより、第1引数keysで指定した列をインデックスに設定される。

表示行数・列数の設定

表示行数・列数の省略

行数・列数が多いDataFrameを表示させると、途中を省略して表示する。デフォルトで行数は60行を超えると省略され、列数は画面幅に応じて調整される。以下のコードは、pandasのオプションでdisplay.max_rowsとdisplay.max_columnsも表示させている。

import numpy as np
import pandas as pd
import string

n_rows = 61
n_columns = 20
data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]
df = pd.DataFrame(data, columns=column_names)

print(df)

print("max rows:{}".format(pd.options.display.max_rows))
print("max_cols:{}".format(pd.options.display.max_columns))

#       A    B    C    D    E    F    G  ...    N    O    P    Q    R    S    T
# 0     0    1    2    3    4    5    6  ...   13   14   15   16   17   18   19
# 1    10   11   12   13   14   15   16  ...   23   24   25   26   27   28   29
# 2    20   21   22   23   24   25   26  ...   33   34   35   36   37   38   39
# 3    30   31   32   33   34   35   36  ...   43   44   45   46   47   48   49
# 4    40   41   42   43   44   45   46  ...   53   54   55   56   57   58   59
# ..  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...
# 56  560  561  562  563  564  565  566  ...  573  574  575  576  577  578  579
# 57  570  571  572  573  574  575  576  ...  583  584  585  586  587  588  589
# 58  580  581  582  583  584  585  586  ...  593  594  595  596  597  598  599
# 59  590  591  592  593  594  595  596  ...  603  604  605  606  607  608  609
# 60  600  601  602  603  604  605  606  ...  613  614  615  616  617  618  619
# 
# [61 rows x 20 columns]
# max rows:60
# max_cols:0

import numpy as np

import pandas as pd

import string

n_rows = 61

n_columns = 20

data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]

df = pd.DataFrame(data, columns=column_names)

print(df)

print("max rows:{}".format(pd.options.display.max_rows))

print("max_cols:{}".format(pd.options.display.max_columns))

# A B C D E F G ... N O P Q R S T

# 0 0 1 2 3 4 5 6 ... 13 14 15 16 17 18 19

# 1 10 11 12 13 14 15 16 ... 23 24 25 26 27 28 29

# 2 20 21 22 23 24 25 26 ... 33 34 35 36 37 38 39

# 3 30 31 32 33 34 35 36 ... 43 44 45 46 47 48 49

# 4 40 41 42 43 44 45 46 ... 53 54 55 56 57 58 59

# .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

# 56 560 561 562 563 564 565 566 ... 573 574 575 576 577 578 579

# 57 570 571 572 573 574 575 576 ... 583 584 585 586 587 588 589

# 58 580 581 582 583 584 585 586 ... 593 594 595 596 597 598 599

# 59 590 591 592 593 594 595 596 ... 603 604 605 606 607 608 609

# 60 600 601 602 603 604 605 606 ... 613 614 615 616 617 618 619

# [61 rows x 20 columns]

# max rows:60

# max_cols:0

この場合、行数に61行をしているので行表示は省略され、列数はコンソールの幅に応じて省略されている（コンソールの幅を変えて実行すると、その幅に応じて納めようと省略される）。

表示行数の設定

表示させる最大行数を変更するには、pandas.set_option()でdisplay.max_rows属性を設定する。

import numpy as np
import pandas as pd
import string

n_rows = 100
n_columns = 20
data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]
df = pd.DataFrame(data, columns=column_names)

pd.set_option('display.max_rows', 100)
print(df)

#       A    B    C    D    E    F    G  ...     N     O     P     Q     R     S     T
# 0     0    1    2    3    4    5    6  ...    13    14    15    16    17    18    19
# 1    10   11   12   13   14   15   16  ...    23    24    25    26    27    28    29
# 2    20   21   22   23   24   25   26  ...    33    34    35    36    37    38    39
# 3    30   31   32   33   34   35   36  ...    43    44    45    46    47    48    49
# 4    40   41   42   43   44   45   46  ...    53    54    55    56    57    58    59
# ・・・この間の全ての行が表示される・・・
# 95  950  951  952  953  954  955  956  ...   963   964   965   966   967   968   969
# 96  960  961  962  963  964  965  966  ...   973   974   975   976   977   978   979
# 97  970  971  972  973  974  975  976  ...   983   984   985   986   987   988   989
# 98  980  981  982  983  984  985  986  ...   993   994   995   996   997   998   999
# 99  990  991  992  993  994  995  996  ...  1003  1004  1005  1006  1007  1008  1009

[100 rows x 20 columns]

import numpy as np

import pandas as pd

import string

n_rows = 100

n_columns = 20

data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]

df = pd.DataFrame(data, columns=column_names)

pd.set_option('display.max_rows', 100)

print(df)

# A B C D E F G ... N O P Q R S T

# 0 0 1 2 3 4 5 6 ... 13 14 15 16 17 18 19

# 1 10 11 12 13 14 15 16 ... 23 24 25 26 27 28 29

# 2 20 21 22 23 24 25 26 ... 33 34 35 36 37 38 39

# 3 30 31 32 33 34 35 36 ... 43 44 45 46 47 48 49

# 4 40 41 42 43 44 45 46 ... 53 54 55 56 57 58 59

# ・・・この間の全ての行が表示される・・・

# 95 950 951 952 953 954 955 956 ... 963 964 965 966 967 968 969

# 96 960 961 962 963 964 965 966 ... 973 974 975 976 977 978 979

# 97 970 971 972 973 974 975 976 ... 983 984 985 986 987 988 989

# 98 980 981 982 983 984 985 986 ... 993 994 995 996 997 998 999

# 99 990 991 992 993 994 995 996 ... 1003 1004 1005 1006 1007 1008 1009

[100 rows x 20 columns]

表示列数の設定

表示させる最大列数を設定するには、pandas.set_option()でdisplay.max_columns属性を設定する。以下の例では20列すべてを表示させていて、コンソールの幅に収まらない列は表単位で改行されている。

import numpy as np
import pandas as pd
import string

n_rows = 100
n_columns = 20
data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]
df = pd.DataFrame(data, columns=column_names)

pd.set_option('display.max_columns', 20)
print(df)

#       A    B    C    D    E    F    G    H    I    J     K     L     M     N  \
# 0     0    1    2    3    4    5    6    7    8    9    10    11    12    13   
# 1    10   11   12   13   14   15   16   17   18   19    20    21    22    23   
# 2    20   21   22   23   24   25   26   27   28   29    30    31    32    33   
# 3    30   31   32   33   34   35   36   37   38   39    40    41    42    43   
# 4    40   41   42   43   44   45   46   47   48   49    50    51    52    53   
# ..  ...  ...  ...  ...  ...  ...  ...  ...  ...  ...   ...   ...   ...   ...   
# 95  950  951  952  953  954  955  956  957  958  959   960   961   962   963   
# 96  960  961  962  963  964  965  966  967  968  969   970   971   972   973   
# 97  970  971  972  973  974  975  976  977  978  979   980   981   982   983   
# 98  980  981  982  983  984  985  986  987  988  989   990   991   992   993   
# 99  990  991  992  993  994  995  996  997  998  999  1000  1001  1002  1003   
# 
#        O     P     Q     R     S     T  
# 0     14    15    16    17    18    19  
# 1     24    25    26    27    28    29  
# 2     34    35    36    37    38    39  
# 3     44    45    46    47    48    49  
# 4     54    55    56    57    58    59  
# ..   ...   ...   ...   ...   ...   ...  
# 95   964   965   966   967   968   969  
# 96   974   975   976   977   978   979  
# 97   984   985   986   987   988   989  
# 98   994   995   996   997   998   999  
# 99  1004  1005  1006  1007  1008  1009  
# 
# [100 rows x 20 columns]

import numpy as np

import pandas as pd

import string

n_rows = 100

n_columns = 20

data = np.array([[r * 10 + c for c in range(n_columns)] for r in range(n_rows)])

column_names = list(string.ascii_letters)[26 : 26 + n_columns]

df = pd.DataFrame(data, columns=column_names)

pd.set_option('display.max_columns', 20)

print(df)

# A B C D E F G H I J K L M N \

# 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13

# 1 10 11 12 13 14 15 16 17 18 19 20 21 22 23

# 2 20 21 22 23 24 25 26 27 28 29 30 31 32 33

# 3 30 31 32 33 34 35 36 37 38 39 40 41 42 43

# 4 40 41 42 43 44 45 46 47 48 49 50 51 52 53

# .. ... ... ... ... ... ... ... ... ... ... ... ... ... ...

# 95 950 951 952 953 954 955 956 957 958 959 960 961 962 963

# 96 960 961 962 963 964 965 966 967 968 969 970 971 972 973

# 97 970 971 972 973 974 975 976 977 978 979 980 981 982 983

# 98 980 981 982 983 984 985 986 987 988 989 990 991 992 993

# 99 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003

# O P Q R S T

# 0 14 15 16 17 18 19

# 1 24 25 26 27 28 29

# 2 34 35 36 37 38 39

# 3 44 45 46 47 48 49

# 4 54 55 56 57 58 59

# .. ... ... ... ... ... ...

# 95 964 965 966 967 968 969

# 96 974 975 976 977 978 979

# 97 984 985 986 987 988 989

# 98 994 995 996 997 998 999

# 99 1004 1005 1006 1007 1008 1009

# [100 rows x 20 columns]

ファイルの読み込み

CSVファイル

DataFrameにCSVファイルの読み込みには、pandas.read_csv()を使う。

pandas.read_csv(path): pathは読み込むCSVのパス

ヘッダー付きCSVファイル

たとえば、以下のようなヘッダー付きのCSVファイル(ex_basic_w_header.csv)を考える。

name,age
Austine,25
Bill,16
Charly,51

name,age

Austine,25

Bill,16

Charly,51

このファイルが実行ファイルと同じディレクトリにある場合、以下のように__file__を使って読み込むとよい。

データには自動的にインデックス番号が付加される。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_w_header.csv")

df = pd.read_csv(path)

print(df)

#       name  age
# 0  Austine   25
# 1     Bill   16
# 2   Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_w_header.csv")

df = pd.read_csv(path)

print(df)

# name age

# 0 Austine 25

# 1 Bill 16

# 2 Charly 51

ヘッダー無しCSVファイル

以下のようなヘッダーがないファイルの場合。

Austine,25
Bill,16
Charly,51

Austine,25

Bill,16

Charly,51

そのまま読み込んでしまうと1行目がヘッダーと解釈されてしまう。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")
df = pd.read_csv(path)
print(df)

#   Austine  25
# 0    Bill  16
# 1  Charly  51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")

df = pd.read_csv(path)

print(df)

# Austine 25

# 0 Bill 16

# 1 Charly 51

引数にheader=Noneを指定すると1行目からデータとして読み込み、列名には番号が振られる。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")
df = pd.read_csv(path, header=None)
print(df)

#          0   1
# 0  Austine  25
# 1     Bill  16
# 2   Charly  51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")

df = pd.read_csv(path, header=None)

print(df)

# 0 1

# 0 Austine 25

# 1 Bill 16

# 2 Charly 51

引数としてnames=(列名1, 列名2, ...)を指定すると、ヘッダー無しとして読み込まれ、列名がセットされる。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")
df = pd.read_csv(path, names=("name", "age"))
print(df)

#       name  age
# 0  Austine   25
# 1     Bill   16
# 2   Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_wo_header.csv")

df = pd.read_csv(path, names=("name", "age"))

print(df)

# name age

# 0 Austine 25

# 1 Bill 16

# 2 Charly 51

行のスキップ

以下のように、先頭から何行か読み飛ばしたいファイルの時。

File: employees lest
Date: 2020/04/01
name,age
Austine,25
Bill,16
Charly,51

File: employees lest

Date: 2020/04/01

name,age

Austine,25

Bill,16

Charly,51

引数にskiprowsでスキップする行数を指定する。このとき、最初の行はヘッダーとして解釈される。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skiprows.csv")
df = pd.read_csv(path, skiprows=2)
print(df)

#       name  age
# 0  Austine   25
# 1     Bill   16
# 2   Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skiprows.csv")

df = pd.read_csv(path, skiprows=2)

print(df)

# name age

# 0 Austine 25

# 1 Bill 16

# 2 Charly 51

ヘッダー行の指定

ヘッダー行を含むファイルでヘッダーの開始行を指定したいときはheaderで開始位置を指定する。指定したヘッダーより前の行は無視される。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skiprows.csv")
df = pd.read_csv(path, header=2)
print(df)

#       name  age
# 0  Austine   25
# 1     Bill   16
# 2   Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skiprows.csv")

df = pd.read_csv(path, header=2)

print(df)

# name age

# 0 Austine 25

# 1 Bill 16

# 2 Charly 51

インデックス列の指定

以下のファイルは通し番号付きで、番号には列名がない(1行目の1列目が空)。

,order,name,age
1, first, Austine,25
2, second, Bill,16
3, third, Charly,51

,order,name,age

1, first, Austine,25

2, second, Bill,16

3, third, Charly,51

これをそのままデータフレームに読み込むと、1列目もデータと解釈されてインデックスが自動生成される。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")
df = pd.read_csv(path)
print(df)

#    Unnamed: 0    order      name  age
# 0           1    first   Austine   25
# 1           2   second      Bill   16
# 2           3    third    Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")

df = pd.read_csv(path)

print(df)

# Unnamed: 0 order name age

# 0 1 first Austine 25

# 1 2 second Bill 16

# 2 3 third Charly 51

引数にindex_col=0を指定すると、その列がインデックスとして認識される。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")
df = pd.read_csv(path, index_col=0)
print(df)

#      order      name  age
# 1    first   Austine   25
# 2   second      Bill   16
# 3    third    Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")

df = pd.read_csv(path, index_col=0)

print(df)

# order name age

# 1 first Austine 25

# 2 second Bill 16

# 3 third Charly 51

index_colを1以上の値にすると、それ以前の列は読み込まれない。ただし指定した列に列名が定義されていると、それもデータとみなされてしまう。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")
df = pd.read_csv(path, index_col=1)
print(df)

#          Unnamed: 0      name  age
# order                             
#  first            1   Austine   25
#  second           2      Bill   16
#  third            3    Charly   51

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_skipcols.csv")

df = pd.read_csv(path, index_col=1)

print(df)

# Unnamed: 0 name age

# order

# first 1 Austine 25

# second 2 Bill 16

# third 3 Charly 51

日本語

日本語などマルチバイトの文字を含む場合、対応する文字コードを指定する。

import os
import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_jp.csv")
df = pd.read_csv(path, encoding='SHIFT-JIS')
print(df)

#    名前  年齢
# 0  井上  25
# 1  田中  44
# 2  武藤  16

import os

import pandas as pd

path = os.path.join(os.path.dirname(__file__), "ex_basic_jp.csv")

df = pd.read_csv(path, encoding='SHIFT-JIS')

print(df)

# 名前年齢

# 0 井上 25

# 1 田中 44

# 2 武藤 16

One-hot-encoding

DataFrameのget_dummies()メソッドは、属性データをone-hotの形にエンコードしてくれる。

Tips – 注意点など

配列で生成しない方がいい

コード上で簡単なDataFrameを生成するとき、配列で数値と文字列を混在させるとトラブルになる。

DataFrameの行追加の速さ

DataFrameに行を追加する場合、基本的にはリストに変換してリストの状態で行を追加し、それをDataFrameに変換するのが最も速い。いくつかの方法による速さの違いはこちら。

行単位／列単位の合計・率の計算

DataFrameオブジェクトの行単位／列単位の合計や、それらを使った率の計算方法。

ndarray – 配列による要素指定

2019-10-27 / tau / コメントする

“Pythonではじめる機械学習”中、27番のコードで気になったので調べた結果。

Scitkit-learnを使ってk-最近傍法の予測結果を保存し、その結果を使って予測されたアヤメの種類を表示させている。

prediction = knn.predict(X_new)
print("Prediction: {}".format(prediction))
print("Predicted target name] {}".format( \
    iris_dataset['target_names'][prediction]))

# Prediction: [0]
# Predicted target name] ['setosa']

prediction = knn.predict(X_new)

print("Prediction: {}".format(prediction))

print("Predicted target name] {}".format( \

iris_dataset['target_names'][prediction]))

# Prediction: [0]

# Predicted target name] ['setosa']

ここでprediction、iris_dataset['target_names']のいずれの型もnumpy.ndarrayであり、ndarrayの引数に整数ではなくてndarrayを使っている。

通常のリストでこれをやると、”リストのインデックスにリストを使ってはダメ”とエラーになる。

a = ['a', 'b', 'c']
print(a)

x = 0
print(a[x])

y = [0]
print(a[y])

# ['a', 'b', 'c']
# a
# ...
# TypeError: list indices must be integers or slices, not list

a = ['a', 'b', 'c']

print(a)

x = 0

print(a[x])

y = [0]

print(a[y])

# ['a', 'b', 'c']

# a

# ...

# TypeError: list indices must be integers or slices, not list

ところがndarrayの場合はその引数にndarrayを渡すことができて、結果はndarrayとして帰ってくる。

import numpy as np

a = np.array(['a', 'b', 'c'])

x = 0
print("{}: {}".format(x, a[x]))

y = np.array([0])
print("{}: {}".format(y, a[y]))

# 0: a
# [0]: ['a']

import numpy as np

a = np.array(['a', 'b', 'c'])

x = 0

print("{}: {}".format(x, a[x]))

y = np.array([0])

print("{}: {}".format(y, a[y]))

# 0: a

# [0]: ['a']

さらに、引数に渡す配列が複数の要素を持つ場合、各要素を引数とした場合に対応する元の配列の要素が配列として返される。

z = np.array([0, 2, 2, 1])
print("{}: {}".format(z, a[z]))

# [0 2 2 1]: ['a' 'c' 'c' 'b']

z = np.array([0, 2, 2, 1])

print("{}: {}".format(z, a[z]))

# [0 2 2 1]: ['a' 'c' 'c' 'b']

なお、元の配列がndarrayであれば、引数に普通のリストを渡しても同じ結果が得られる。

u = [0, 2, 2, 1]
print("{}: {}".format(u, a[u]))

# [0, 2, 2, 1]: ['a' 'c' 'c' 'b']

u = [0, 2, 2, 1]

print("{}: {}".format(u, a[u]))

# [0, 2, 2, 1]: ['a' 'c' 'c' 'b']

Python3 – os/os.path

2019-10-26 / tau / コメントする

主な関数

os.getcwd(): カレントディレクトリー。プログラム実行直後は実行中のディレクトリーを指している。実行ファイルのディレクトリー情報を得るには__file__を使うとよい。
os.path.dirname(dir): dirのディレクトリーのフルパス。
os.listdir(dir): dirにあるファイル・ディレクトリーのリスト。
os.chdir(dir): dirに移動。存在しない場合は’NotADirectoryError’をスローする。

実行例

import sys
import os

if len(sys.argv) > 1:
    target_directory = sys.argv[1]
    try:
        os.chdir(target_directory)
    except NotADirectoryError as e:
        print("Error: Directory not exists")
        sys.exit()

print("Specified directory: {}".format(target_directory))
print()
cwd = os.getcwd()
print('current working directory:', cwd)
print('directory name           :', os.path.dirname(cwd))
print('list of directories      :', os.listdir(cwd))

import sys

import os

if len(sys.argv) > 1:

target_directory = sys.argv[1]

try:

os.chdir(target_directory)

except NotADirectoryError as e:

print("Error: Directory not exists")

sys.exit()

print("Specified directory: {}".format(target_directory))

print()

cwd = os.getcwd()

print('current working directory:', cwd)

print('directory name :', os.path.dirname(cwd))

print('list of directories :', os.listdir(cwd))

実行結果

C:\...\python\packages\os>test_os.py "C:\...\python\packages\os"
Specified directory: C:\...\python\packages\os

current working directory: C:\...\python\packages\os
directory name           : C:\...\python\packages
list of directories      : ['dir1', 'dir2', 'test-01.txt', 'test-02.txt', 'test_os.py']

C:\...\python\packages\os>test_os.py "C:\...\python\packages\os"

Specified directory: C:\...\python\packages\os

current working directory: C:\...\python\packages\os

directory name : C:\...\python\packages

list of directories : ['dir1', 'dir2', 'test-01.txt', 'test-02.txt', 'test_os.py']

ファイル／ディレクトリーの判定

ファイルの判定はos.path.isfile(target)。ディレクトリーの判定はos.path.isdir(target)。

print("\nFile or directory")
for file in os.listdir(cwd):
    if os.path.isfile(file):
        print('f ', end='')
    else:
        print('d ', end='')
    print(file)

print("\nFile or directory")

for file in os.listdir(cwd):

if os.path.isfile(file):

print('f ', end='')

else:

print('d ', end='')

print(file)

実行結果

File or directory
d dir1
d dir2
f test-01.txt
f test-02.txt
f test_os.py

File or directory

d dir1

d dir2

f test-01.txt

f test-02.txt

f test_os.py

Python3 – sys

2019-10-26 / tau / コメントする

プログラムの停止

プログラムを停止するのはsys.exit()。

import sys

args = sys.argv

if len(args) == 1:
    print("No arguments, system exits.")
    sys.exit()
else:
    print("Arguments are {}".format(args[1:]))

# C:...\python\test\sys>exit.py
# No arguments, system exits.
# 
# C:...\python\test\sys>exit.py 1 2
# Arguments are ['1', '2']

import sys

args = sys.argv

if len(args) == 1:

print("No arguments, system exits.")

sys.exit()

else:

print("Arguments are {}".format(args[1:]))

# C:...\python\test\sys>exit.py

# No arguments, system exits.

# C:...\python\test\sys>exit.py 1 2

# Arguments are ['1', '2']

sys.argv～コマンドライン引数

sys.argvはコマンドライン引数を配列で返す。0番目の値は実行中のパス付のスクリプト名自体。

args = sys.argv

print('number of afgs {}'.format(len(args)))
print(args)
for arg in args:
    print(arg)

# C:...\python\test\sys>cmd_arg.py one two
# number of afgs 3
# ['C:...\\python\\test\\sys\\cmd_arg.py', 'one', 'two']
# 0 C:\Users\tomo\Google ドライブ\IT_and_Mobile\dev\python\test\sys\cmd_arg.py
# 1 one
# 2 two

args = sys.argv

print('number of afgs {}'.format(len(args)))

print(args)

for arg in args:

print(arg)

# C:...\python\test\sys>cmd_arg.py one two

# number of afgs 3

# ['C:...\\python\\test\\sys\\cmd_arg.py', 'one', 'two']

# 0 C:\Users\tomo\Google ドライブ\IT_and_Mobile\dev\python\test\sys\cmd_arg.py

# 1 one

# 2 two

Python3 – 正規表現 – group()

2019-10-22 / tau / コメントする

たとえば次のようなファイル名のテキストがあるとする。

file_name-10.txt
file_name-1.txt

ファイル名本体の末尾にある番号を2桁に統一したいようなとき、1つ目にはマッチせず、2つ目にはマッチさせたい。

この場合、以下のような正規表現でマッチングできる。

str1 = 'file_name-10.txt'
str2 = 'file_name-1.txt'

pattern = re.compile(r'-\d\.')

match = re.search(pattern, str1)
print(match)
match = re.search(pattern, str2)
print(match)

# None
# <re.Match object; span=(9, 12), match='-1.'>

str1 = 'file_name-10.txt'

str2 = 'file_name-1.txt'

pattern = re.compile(r'-\d\.')

match = re.search(pattern, str1)

print(match)

match = re.search(pattern, str2)

print(match)

# None

# <re.Match object; span=(9, 12), match='-1.'>

ただしこれだけでは、該当するファイル名はわかるが、0の挿入といった部分的な操作ができない。

そのような場合は、正規表現を()で区切り、group()メソッドで部分列を取り出すことができる。

pattern = re.compile(r'(\w+-)(\d\.\w+)')

match = re.search(pattern, str1)
print(match)
match = re.search(pattern, str2)
print(match)

print(match.group(0))
print(match.group(1))
print(match.group(2))

print(match.group(1) + '0' + match.group(2))

# None
# <re.Match object; span=(0, 15), match='file_name-1.txt'>
# file_name-1.txt
# file_name-
# 1.txt
# file_name-01.txt

pattern = re.compile(r'(\w+-)(\d\.\w+)')

match = re.search(pattern, str1)

print(match)

match = re.search(pattern, str2)

print(match)

print(match.group(0))

print(match.group(1))

print(match.group(2))

print(match.group(1) + '0' + match.group(2))

# None

# <re.Match object; span=(0, 15), match='file_name-1.txt'>

# file_name-1.txt

# file_name-

# 1.txt

# file_name-01.txt

パターン設定で()で区切った部分ごとにグルーピングされ、その各部分を後から再利用できる。なお、group(0)はマッチした部分全体になる。

Python3 – enumerateでリストのインデックスが得られる

2019-10-22 / tau / コメントする

通常、リストの要素を順番に操作するときにはforループを使う。

names = ['JP', 'US', 'EU']
for name in names:
    print(name)

# JP
# US
# EU

names = ['JP', 'US', 'EU']

for name in names:

print(name)

# JP

# US

# EU

enumerate()関数を使うと、リストの要素とそのインデックスを同時に得ることができる。

for i, name in enumerate(names):
    print(i, name)

# 0 JP
# 1 US
# 2 EU

for i, name in enumerate(names):

print(i, name)

# 0 JP

# 1 US

# 2 EU

このインデックスにformat()を使うと書式を設定でき、ファイル名のrenameなどに便利。

for i, name in enumerate(names):
    print('{0:02d}'.format(i) + '-' + name)

# 00-JP
# 01-US
# 02-EU

for i, name in enumerate(names):

print('{0:02d}'.format(i) + '-' + name)

# 00-JP

# 01-US

# 02-EU

Python3 – 正規表現の操作

2019-10-22 / tau / コメントする

主なreモジュール関数

まず、reモジュール関数の操作をまとめる。以下の文字列をターゲットにする。

import re
str = 'The rain in spain stays mainly in the plain.'

1 2	import re str = 'The rain in spain stays mainly in the plain.'

re.match()はパターンが先頭でマッチするかどうか。

print(re.match(r'The', str))
print(re.match(r'the', str))

# <re.Match object; span=(0, 3), match='The'>
# None

print(re.match(r'The', str))

print(re.match(r'the', str))

# <re.Match object; span=(0, 3), match='The'>

# None

re.search()はパターンが含まれるかどうか。最初に現れたパターンにのみマッチする。

print(re.search(r'in', str))
print(re.search(r'inn', str))

# <re.Match object; span=(6, 8), match='in'>
# None

print(re.search(r'in', str))

print(re.search(r'inn', str))

# <re.Match object; span=(6, 8), match='in'>

# None

re.findall()は一致するパターン全てのリストを返す。

print(re.findall(r'in', str))
print(re.findall(r'inn', str))

# ['in', 'in', 'in', 'in', 'in', 'in']
# []

print(re.findall(r'in', str))

print(re.findall(r'inn', str))

# ['in', 'in', 'in', 'in', 'in', 'in']

# []

re.finditer()は一致するパターンのイテレータを返す。

for s in re.finditer(r'in', str):
    print(s)

# <re.Match object; span=(6, 8), match='in'>
# <re.Match object; span=(9, 11), match='in'>
# <re.Match object; span=(15, 17), match='in'>
# <re.Match object; span=(26, 28), match='in'>
# <re.Match object; span=(31, 33), match='in'>
# <re.Match object; span=(41, 43), match='in'>

for s in re.finditer(r'in', str):

print(s)

# <re.Match object; span=(6, 8), match='in'>

# <re.Match object; span=(9, 11), match='in'>

# <re.Match object; span=(15, 17), match='in'>

# <re.Match object; span=(26, 28), match='in'>

# <re.Match object; span=(31, 33), match='in'>

# <re.Match object; span=(41, 43), match='in'>

re.sub()は一致するパターンを置き換え。

print(re.sub(r'in', 'IN', str))

# The raIN IN SpaIN stays maINly IN the plaIN.

print(re.sub(r'in', 'IN', str))

# The raIN IN SpaIN stays maINly IN the plaIN.

re.subn()は一致するパターンを置き換え、その結果と置換回数のタプルを返す。

print(re.subn(r'in', 'IN', str))

# ('The raIN IN SpaIN stays maINly IN the plaIN.', 6)

print(re.subn(r'in', 'IN', str))

# ('The raIN IN SpaIN stays maINly IN the plaIN.', 6)

コンパイル

パターン文字列をコンパイルしパターンオブジェクト化することで、再利用・高速化が可能。この場合、reモジュール関数と同じ名前のメソッドが使える。

pattern = re.compile(r'in')
print(pattern.search(str))
print(pattern.findall(str))
print(pattern.sub('IN', str))
print(pattern.subn('IN', str))

# <re.Match object; span=(6, 8), match='in'>
# ['in', 'in', 'in', 'in', 'in', 'in']
# The raIN IN SpaIN stays maINly IN the plaIN.
# ('The raIN IN SpaIN stays maINly IN the plaIN.', 6)

pattern = re.compile(r'in')

print(pattern.search(str))

print(pattern.findall(str))

print(pattern.sub('IN', str))

print(pattern.subn('IN', str))

# <re.Match object; span=(6, 8), match='in'>

# ['in', 'in', 'in', 'in', 'in', 'in']

# The raIN IN SpaIN stays maINly IN the plaIN.

# ('The raIN IN SpaIN stays maINly IN the plaIN.', 6)

マッチオブジェクトの利用

上記のうちmatch()、search()、findall()はマッチオブジェクトを返す。マッチオブジェクトの主なメソッドには、マッチした開始点を返すstart()、終了点(+1)を返すend()、それらをタプルで範囲として返すspan()、マッチした文字列を返すgroup()がある。

str = 'Peter piper picked a peck of pickled pepper.'
pattern = re.compile(r'[Pp]\w+r')
m = pattern.search(str)
print(m.start(), m.end(), m.span(), m.group())

# 0 5 (0, 5) Peter

str = 'Peter piper picked a peck of pickled pepper.'

pattern = re.compile(r'[Pp]\w+r')

m = pattern.search(str)

print(m.start(), m.end(), m.span(), m.group())

# 0 5 (0, 5) Peter

複数のマッチした文字列を処理するには、finditer()で順次マッチオブジェクトを取り出すとよい。

for m in pattern.finditer(str):
    print(m.start(), m.end(), m.span(), m.group())

# 0 5 (0, 5) Peter
# 6 11 (6, 11) piper
# 37 43 (37, 43) pepper

for m in pattern.finditer(str):

print(m.start(), m.end(), m.span(), m.group())

# 0 5 (0, 5) Peter

# 6 11 (6, 11) piper

# 37 43 (37, 43) pepper

グラフの描画

pyplot

figure, axes

グラフの種類

3次元グラフ

tips

概要

ライブラリーのインポート

描画する関数

各種設定

タイトルと軸ラベル

軸の範囲

軸目盛

グリッド(補助線)

グラフの描画

凡例の表示

グラフの表示

概要

情報・内容の取得

データの概観

基本的なパラメーターの取得

DataFrameの生成

要素の操作

列の操作

行の操作

DataFrameで直接行を指定して参照

maskによる行の抽出

queryによる行の抽出

行の追加

1行追加する場合

複数行追加する場合

DataFrameの結合

cocatメソッド～縦方向の結合

joinメソッド～横方向の結合

合計の計算と合計欄

ソート

sort_values()～列名を指定してソート

ascendingパラメーター

reset_index()～インデックスの降り直し

複数列によるソート

axisの方向

DataFrameの設定

列のインデックス設定

表示行数・列数の設定

表示行数・列数の省略

表示行数の設定

表示列数の設定

ファイルの読み込み

CSVファイル

ヘッダー付きCSVファイル

ヘッダー無しCSVファイル

行のスキップ

ヘッダー行の指定

インデックス列の指定

日本語

One-hot-encoding

Tips – 注意点など

配列で生成しない方がいい

DataFrameの行追加の速さ

行単位／列単位の合計・率の計算

主な関数

ファイル／ディレクトリーの判定

プログラムの停止

sys.argv～コマンドライン引数

主なreモジュール関数

コンパイル

マッチオブジェクトの利用

`sort_values()`～列名を指定してソート

`ascending`パラメーター

`reset_index()`～インデックスの降り直し