概要
2次元配列をデータテーブルのように使っていて、行や列を追加する場合の方法を整理。
リストの場合とndarrayの場合それぞれについて、行の追加、列の追加のためのメソッドや関数と、その使い方の注意を記しておく。
結論として、ndarrayを使う場合はnumpy.vstack()関数、numpy.hstack()関数を用いるのが、配列の2次元化や追加方向のaxis指定がなく紛れがない。
リストの場合
リストの場合はappend()メソッド、insert()メソッドで行や列を追加する。ただし、より現実的な方法をこちらに整理した。
注意点
- リストの
append()メソッド、insert()メソッドは元のリストを書き換える
- 各メソッドは戻り値を持たない(
None)
- 初期データが1行/1列の場合に2次元配列であることを明示する必要がある
初期リストが空の場合は単に1次元の空のリストを準備すればいいので、初期リストがある場合でも、空のリストを準備してからそこに追加するように決めておけばミスは減りそう。
行の追加
append()メソッド
append()メソッドは素直に引数のリストをもとのリストに追加する。ただし、下のコードの1行目のように元のリストが2次元配列であることを明示しなければならない。
|
|
a = [[0, 1, 2]] print(a) b = [3, 4, 5] a.append(b) print(a) # [[0, 1, 2]] # [[0, 1, 2], [3, 4, 5]] |
以下は失敗。元のリストを単なる要素リストで定義してしまうと、追加するリストが要素の一つとして扱われてしまう。
|
|
a = [0, 1, 2] print(a) b = [3, 4, 5] a.append(b) print(a) # [0, 1, 2] # [0, 1, 2, [3, 4, 5]] |
空のリストへの追加。
この場合は1次元の空のリストを用意すれば、追加されるリストが要素として順次追加されていく。
|
|
a = [] print(a) b = [0, 1, 2] a.append(b) print(a) b = [3, 4, 5] a.append(b) print(a) # [] # [[0, 1, 2]] # [[0, 1, 2], [3, 4, 5]] |
insert()メソッド
insert()メソッドも素直にリストを追加してくれるが、追加位置を指定するのに一手間かかる。行の最後に追加するときは、追加位置をlen(元のリスト)で指定する
その他の仕様はappend()メソッドと同じ。
|
|
a = [[0, 1, 2]] print(a) b = [3, 4, 5] a.insert(len(a), b) print(a) # [[0, 1, 2]] # [[0, 1, 2], [3, 4, 5]] |
空のリストへの追加もappend()メソッドと同様。
|
|
a = [] print(a) b = [0, 1, 2] a.insert(len(a), b) print(a) b = [3, 4, 5] a.insert(len(a), b) print(a) # [] # [[0, 1, 2]] # [[0, 1, 2], [3, 4, 5]] |
列の追加
列の追加の場合、各要素が縦に並んだ列ベクトルとしての定義になる。
append()メソッド
行の追加と同様。最初の1列から定義する場合、明示的に列ベクトルの2次元配列であることを明示する必要がある。
|
|
a = [[[0], [1], [2]]] print(a) b = [[3], [4], [5]] a.append(b) print(a) # [[[0], [1], [2]]] # [[[0], [1], [2]], [[3], [4], [5]]] |
空のリストへの追加の場合は、行の追加と同様シンプル。
|
|
a = [] print(a) b = [[0], [1], [2]] a.append(b) print(a) b = [[3], [4], [5]] a.append(b) print(a) # [] # [[[0], [1], [2]]] # [[[0], [1], [2]], [[3], [4], [5]]] |
insert()メソッド
insert()メソッドの場合も行の追加と同様。
|
|
a = [[[0], [1], [2]]] print(a) b = [[3], [4], [5]] a.insert(len(a), b) print(a) # [[[0], [1], [2]]] # [[[0], [1], [2]], [[3], [4], [5]]] |
空のリストへの追加も行の追加と同様。
|
|
a = [] print(a) b = [[0], [1], [2]] a.insert(len(a), b) print(a) b = [[3], [4], [5]] a.insert(len(a), b) print(a) # [] # [[[0], [1], [2]]] # [[[0], [1], [2]], [[3], [4], [5]]] |
ndarrayの場合
ndarrayの場合は、numpyのモジュール関数append()、insert()のほか、hstack()関数、vstack()関数も使える。
注意点
- リストのメソッドと異なり、
numpyの各モジュール関数は元の配列を変更せず、変更後の新たな配列を戻り値として返す
append()関数、insert()関数では、行の追加/列の追加に応じて引数axisを指定するappend()関数は、行を追加する場合は追加する配列も2次元で明示する必要があるが、列を追加する場合にはそのまま指定する- 空の配列は
empty()関数で準備し、型を指定しておく
hstack()関数、vstack()関数は、元の配列と追加する配列をタプルで指定する
行の追加
ndarrayで行を追加する場合、numpyモジュールのappend()関数、insert()関数でaxis=0を指定するか、vstack()関数を利用する。
numpy.append()関数
初期配列が2次元であることを明示しなければならない点はリストのappend()メソッドと同じだが、追加配列でもこれが必要になる。
numpy.append(元の配列, 追加する配列, axis=0)
- 追加する配列は、元の配列と次元・列数があっていなければならない
→行ベクトルでもndarrayの2次元配列としなければならない
→下記コード例では4行目のnp.array([b])
→こうしないと”次元が合わない”としてエラーになる
- 追加する配列を行として追加する場合は、
axis=0の指定が必須(これを指定しないと、単に元の要素に続いて追加配列の要素が追加されるだけ)
|
|
a = np.array([[0, 1, 2]]) print(a) b = np.array([3, 4, 5]) print(np.append(a, np.array([b]), axis=0)) # [[0 1 2]] # [[0 1 2] # [3 4 5]] |
空の配列への追加の場合、numpy.empty(0, n)で空の配列を準備する。
numpy.empty((行数, 列数), dtype=型)
- 確保する配列の各次元のサイズはタプルで指定
- 行が空なので行数は0で指定
dtype引数で型を明示しないとデフォルトのfloat型になる
|
|
a = np.empty((0, 3), dtype=int) print(a) b = np.array([0, 1, 2]) a = np.append(a, np.array([b]), axis=0) print(a) b = np.array([3, 4, 5]) a = np.append(a, np.array([b]), axis=0) print(a) # [] # [[0 1 2]] # [[0 1 2] # [3 4 5]] |
numpy.insert()関数
リストのinsert()メソッドと同様だが、いくつか注意が必要。
numpy.insert(元の配列, 追加する行位置, 追加する配列, axis=0)
- 追加する位置は最後の行の次の行番号で、これは元の配列の
shapeプロパティーで得られる(shape[0]は配列各次元のサイズで、2次元配列の場合shape[0]は行数、shape[1]は列数を表す)
- 追加する配列はそのまま指定する(2次元で定義しない)
→追加する配列は2次元化しても同じ結果になる
axis=0の指定が必要
|
|
a = np.array([np.array([0, 1, 2])]) print(a) b = np.array([3, 4, 5]) print(np.insert(a, a.shape[0], b, axis=0)) # [[0 1 2]] # [[0 1 2] # [3 4 5]] |
空の配列への追加する場合は、元の配列をnumpy.empty(0, n)で生成。
|
|
a = np.empty((0, 3), dtype=int) print(a) b = np.array([0, 1, 2]) a = np.insert(a, a.shape[0], b, axis=0) print(a) b = np.array([3, 4, 5]) a = np.insert(a, a.shape[0], b, axis=0) print(a) # [] # [[0 1 2]] # [[0 1 2] # [3 4 5]] |
numpy.vstack()関数
numpy.vstack()関数は引数に2以上の配列を指定し、それらを縦に連結していく。特に2次元配列化や軸の指定の必要はない。
|
|
a = np.array([0, 1, 2]) print(a) b = np.array([3, 4, 5]) print(np.vstack((a, b))) # [0 1 2] # [[0 1 2] # [3 4 5]] |
空の配列への追加の場合は、numpy.empty(0, n)で生成した空の配列を含めて、順次タプルの中に追加したい配列を指定するだけでよい。
|
|
a = np.empty((0, 3), int) print(a) b = np.array([0, 1, 2]) c = np.array([3, 4, 5]) print(np.vstack((a, b, c))) # [] # [[0 1 2] # [3 4 5]] |
列の追加
ndarrayを列として追加していく場合、追加する配列も列形式である必要がある。列方向の追加をaxis引数で指定する必要がある。
- 通常の行形式の1次元配列を列として追加する場合、
reshape(列数, 1)で列ベクトル化する
- 追加するベクトルを
[]で囲って2次元化する必要はない
axisi=1で列方向の追加として指定
numpy.append()関数
行の追加の時と違って、元の配列も追加する配列も2次元化しない。
|
|
a = np.array([0, 1, 2]).reshape(3, 1) print(a) b = np.array([3, 4, 5]).reshape(3, 1) print(np.append(a, b, axis=1)) # [[0] # [1] # [2]] # [[0 3] # [1 4] # [2 5]] |
空の配列への追加は、列数をゼロとしてnumpy.empty(n, 0)で指定する。
|
|
a = np.empty((3, 0), dtype=int) print(a) b = np.array([0, 1, 2]).reshape(3, 1) a = np.append(a, b, axis=1) print(a) b = np.array([3, 4, 5]).reshape(3, 1) a = np.append(a, b, axis=1) print(a) # [] # [[0] # [1] # [2]] # [[0 3] # [1 4] # [2 5]] |
numpy.insert()関数
numpy.insert()関数も行の追加と同じだが、以下の点に注意。
- 列の追加位置(最後の列の次)は元の変数の
shapeプロパティーの2つ目shape[1]で指定する
- 追加する配列は2次元化せずそのまま指定
- 列方向の追加なので
axis=1を指定する
|
|
a = np.array([0, 1, 2]).reshape(3, 1) print(a) b = np.array([3, 4, 5]) print(np.insert(a, a.shape[1], b, axis=1)) # [[0] # [1] # [2]] # [[0 3] # [1 4] # [2 5]] |
空の配列への追加はこれまでと同様。
|
|
a = np.empty((3, 0), dtype=int) print(a) b = np.array([0, 1, 2]) a = np.insert(a, a.shape[1], b, axis=1) print(a) b = np.array([3, 4, 5]) a = np.insert(a, a.shape[1], b, axis=1) print(a) # [] # [[0] # [1] # [2]] # [[0 3] # [1 4] # [2 5]] |
numpy.hstack()関数
numpy.hstack()関数はvstack()と同様、引数に2以上の配列を指定し、それらを横に連結していく。1次元配列はreshape(-1, 1)などで列ベクトル化する必要がある。
|
|
a = np.array([0, 1, 2]).reshape(3, 1) print(a) b = np.array([3, 4, 5]).reshape(3, 1) print(np.hstack((a, b))) # [[0] # [1] # [2]] # [[0 3] # [1 4] # [2 5]] |
空の配列への追加の場合は、numpy.empty(n, 0)で生成した空の配列から始めて、順次タプルの中に追加したい配列を指定するだけでよい。
|
|
a = np.empty((3, 0), int) print(a) b = np.array([0, 1, 2]).reshape(3, 1) c = np.array([3, 4, 5]).reshape(3, 1) print(np.hstack((a, b, c))) # [] # [[0 3] # [1 4] # [2 5]] |
![]() への線形関係を扱うのに対して、重回帰は複数の説明変数
への線形関係を扱うのに対して、重回帰は複数の説明変数![]() と
と![]() の線形関係を扱う。
の線形関係を扱う。![]() に対して以下の線形式で最も説明性の高いものを求める。
に対して以下の線形式で最も説明性の高いものを求める。![]()
![]() の平方和が最小となるような係数
の平方和が最小となるような係数![]() を最小二乗法により求める。
を最小二乗法により求める。![]() 組が次のように得られているとする。
組が次のように得られているとする。![]()
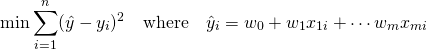
![]() を求めるために、それぞれで偏微分する。
を求めるために、それぞれで偏微分する。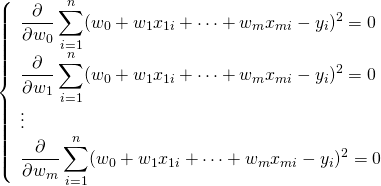
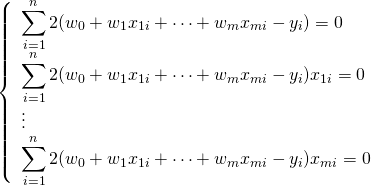
![]() ,
, ![]() ,
, ![]() ,
, ![]() とおいて
とおいて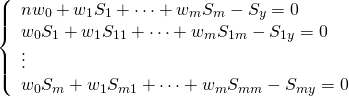
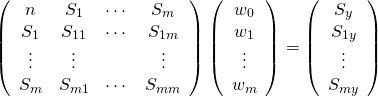
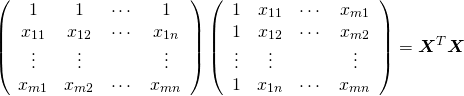
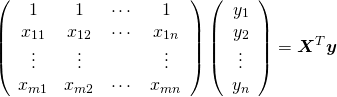
![]()
![]()
![]()
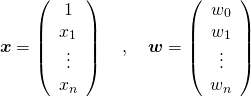
![]()
![]()
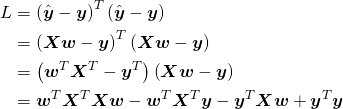
![]()
![]()
![]() は対象行列なので転置しても同じ行列となり、行列の微分の公式から以下のようになることを利用している。
は対象行列なので転置しても同じ行列となり、行列の微分の公式から以下のようになることを利用している。![]()
![]()
![]() を消去する。
を消去する。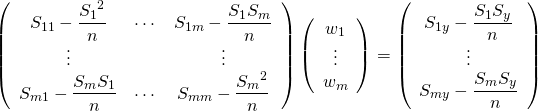
![]() 、
、![]() と表している。
と表している。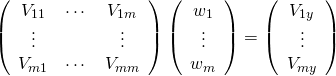
![]() と2つの間に完全な線形関係がある場合、分散・共分散の性質から以下の関係が成り立つ。
と2つの間に完全な線形関係がある場合、分散・共分散の性質から以下の関係が成り立つ。![]()
![Rendered by QuickLaTeX.com \begin{align*} &\left[ \begin{array}{ccccccc} V_{11} & \cdots & V_{1i} & \cdots & V_{1j} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} & \cdots & V_{ij} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{j1} & \cdots & V_{ji} & \cdots & V_{jj} & \cdots & V_{jm}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & V_{mj} & \cdots & V_{mm} \end{array} \right]\\ &= \left[ \begin{array}{ccccccc} V_{11} & \cdots & V_{1i} & \cdots & aV_{1i} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} & \cdots & aV_{ii} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ aV_{i1} & \cdots & aV_{ii} & \cdots & a^2V_{ii} & \cdots & aV_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & aV_{mi} & \cdots & V_{mm} \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-933b818b8ef3c6cf4b6a70d1805f71a8_l3.png)