概要
中心極限定理(central limit theorem: CLT)は、一言で言えば次のようになる。「母集団がどのような確率分布に従うとしても、標本の数を十分大きくしたときには、その合計値あるいは標本平均は、正規分布に従う」
具体的には、母集団の平均を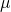 、標準偏差を
、標準偏差を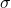 とし、
とし、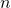 が十分に大きいとき、
が十分に大きいとき、
- 標本の合計
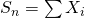 は正規分布
は正規分布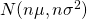 に従う
に従う
- 標本平均
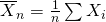 は正規分布
は正規分布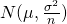 に従う
に従う
表現
中心極限定理は、一般には以下のように表される。
(1) 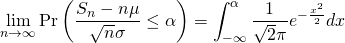
これを少し変形すると、
(2) 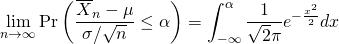
実用
たとえば、サイコロを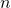 回振った目の合計を考える。全て1(合計が
回振った目の合計を考える。全て1(合計が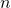 )や全て6(合計が6
)や全て6(合計が6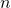 )というケースは稀なので、その間の値になりそうだと予想される。
)というケースは稀なので、その間の値になりそうだと予想される。
中心極限定理を用いると、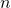 個のサイコロの目の平均と分散より、
個のサイコロの目の平均と分散より、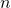 個のサイコロの目の合計は、
個のサイコロの目の合計は、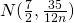 に従うことになる。
に従うことになる。
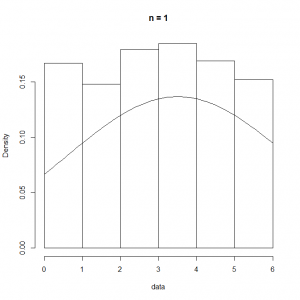
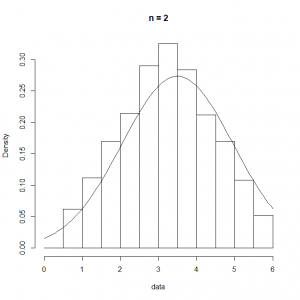
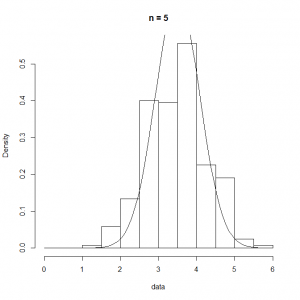
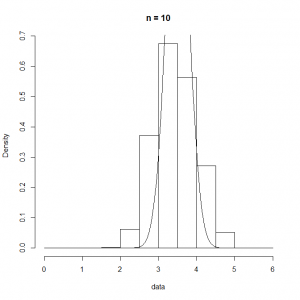
これをRの下記コードで試してみた。一回の試行でサイコロを投げる回数をn.dicesに設定して、その平均を求める試行を1000回繰り返す。
|
|
n.dices <- 5 n.data <- 1000 num.data <- lambda * t.obs data <- c() for (i in 1:n.data) { data <- c(data, mean(as.integer(runif(n.dices, min=1, max=7)))) } ranks <- seq(0, 6, 0.5) hist(data, breaks=ranks, prob=T, main=paste("n =", n.dices)) curve(dnorm(x, 7/2, 35/12/n.dices), add=TRUE) |
n.dicesの回数を変化させた実行結果は以下の通りで、このケースの場合は、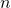 =10程度でもかなり平均の周りに尖った分布となる。
=10程度でもかなり平均の周りに尖った分布となる。
![]()
![]()
![]()
![]()
![]()
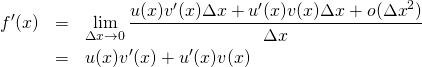
![]()
![]()
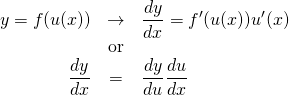
![]() とおくと、
とおくと、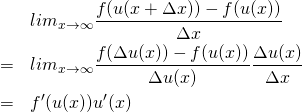
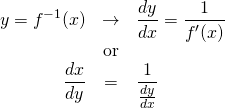
![]()
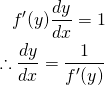
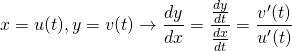
![]() 、
、![]() とおいて、
とおいて、![]()



