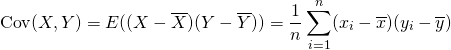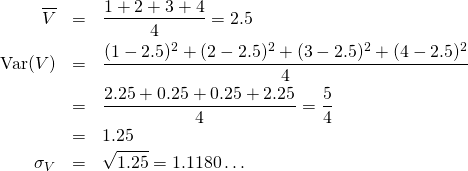単回帰分析～コンビニエンスストア

2019-09-29 / tau / コメントする

概要

Pythonを使った統計計算と図示の練習のため、コンビニエンスストアで単回帰分析をやってみた。

コンビニの店舗数は「商業動態統計年報」の2016年データを使い、説明変数として2015年の国勢調査人口、2018年の国土地理院による都道府県面積、2017年道路統計年報の道路実延長データを使った。

計算コードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt

master_data = np.loadtxt('conv-store-data.csv', delimiter=',',
        skiprows=2, usecols=(1, 2), encoding='utf8')
print(master_data)

y = num_stores = master_data[:,0]
x = population = master_data[:,1]

sxy = np.sum((x - x.mean())*(y - y.mean()))
sxx = np.sum((x - x.mean())**2)
syy = np.sum((y - y.mean())**2)
a = sxy / sxx
b = y.mean() - a*x.mean()
r = sxy / np.sqrt(sxx * syy)
n = len(num_stores)
ESS = n * sxy**2 / sxx
TSS = n * syy
R2 = ESS / TSS

max_population = 15000000
max_stores = 8000
plt.xlim(0, max_population)
plt.ylim(0, max_stores)
plt.xlabel('population')
plt.ylabel('number of stores')

plt.scatter(population, num_stores, label='#stores')

x = np.linspace(0, max_population)
plt.plot(x, a*x + b, color='m')

plt.text(1000000, 7600, 'a = ' + str(a))
plt.text(1000000, 7300, 'b = ' + str(b))
plt.text(1000000, 7000, 'r = '+str(r))
plt.text(1000000, 6700, 'R2 = '+str(R2))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

master_data = np.loadtxt('conv-store-data.csv', delimiter=',',

skiprows=2, usecols=(1, 2), encoding='utf8')

print(master_data)

y = num_stores = master_data[:,0]

x = population = master_data[:,1]

sxy = np.sum((x - x.mean())*(y - y.mean()))

sxx = np.sum((x - x.mean())**2)

syy = np.sum((y - y.mean())**2)

a = sxy / sxx

b = y.mean() - a*x.mean()

r = sxy / np.sqrt(sxx * syy)

n = len(num_stores)

ESS = n * sxy**2 / sxx

TSS = n * syy

R2 = ESS / TSS

max_population = 15000000

max_stores = 8000

plt.xlim(0, max_population)

plt.ylim(0, max_stores)

plt.xlabel('population')

plt.ylabel('number of stores')

plt.scatter(population, num_stores, label='#stores')

x = np.linspace(0, max_population)

plt.plot(x, a*x + b, color='m')

plt.text(1000000, 7600, 'a = ' + str(a))

plt.text(1000000, 7300, 'b = ' + str(b))

plt.text(1000000, 7000, 'r = '+str(r))

plt.text(1000000, 6700, 'R2 = '+str(R2))

plt.show()

人口との関係

コンビニ店舗数と人口の散布図と回帰式を以下に示す。

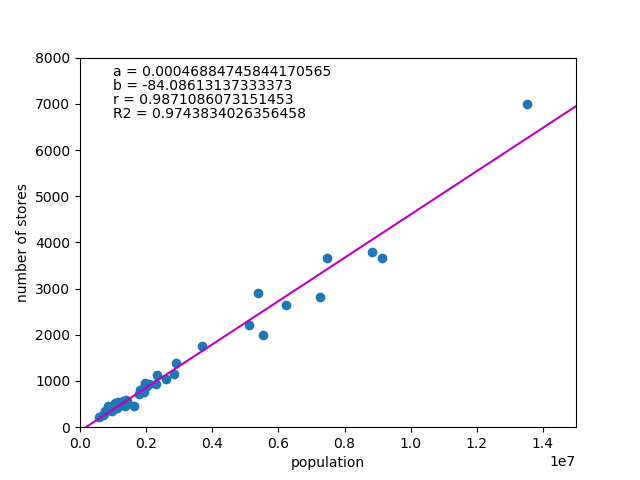
相関係数が極めて高いのは当然で、やはりコンビニの出店計画には人口ファクターが強く作用していることがわかる。

定数項bが店舗数のオーダーに比べてほぼゼロというのも興味深い。

係数aの値からは5万人弱で1店舗ということになるが、人口10万くらいの都市で2店舗しかないことになり、ちょっと少ないような気がする。もしかすると、一定規模以上の市町村単位や都市単位くらいで層化して出店計画を立てているのかもしれない。

面積との関係

店舗数と面積の関係

次に店舗数と都道府県面積の関係を見てみた。

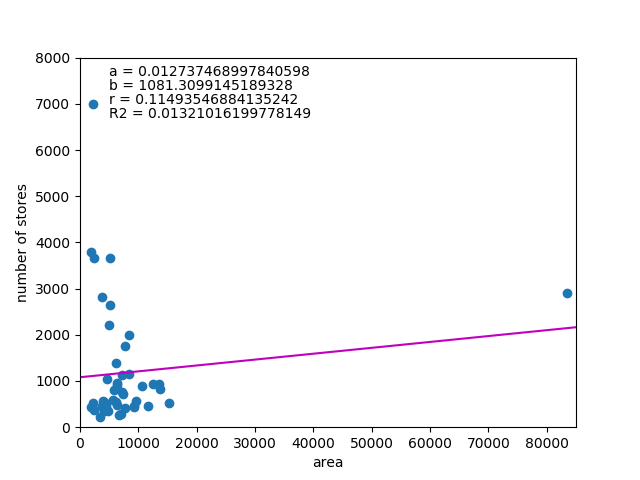
この結果はかなりはずれで、データを見ても人口が少なく面積が群を抜いて大きい北海道の影響を大きく受けている。

ここで、面積が極端に大きい北海道（83423.83㎢～1位、2906店舗～5位）と面積が小さいが集積度が極端に高い東京都（2193.96㎢～45位、7003店舗～1位）の2つを除いて計算してみる。

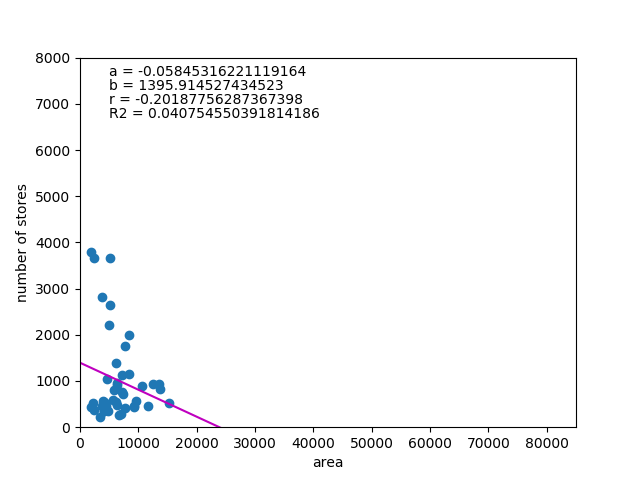
これはさらにおかしな結果で、面積が小さいほど店舗数が多いことになる。

考えてみれば、集客数を期待するなら人口が集積している地域が有利だから、人口密度に比例する可能性を考えた方がいいのかもしれない。もし面積が小さい県の方が集積度が高いと想定すると、面積だけを取り出したときに逆の関係になるとも考えられるが、相関係数や決定係数が小さすぎるので考察は難しい。

人口密度

以下は人口密度との関係。

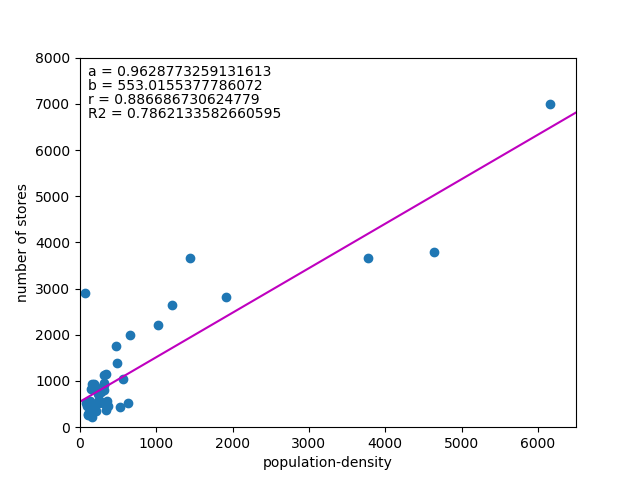
今度はかなりきれいに相関の高さが出ている。

直接的な計算式に入れているかどうかわからないが、GISなどで出店計画を立てるとしたら、人口密度の高いエリアを選んでいくだろうことが想定される。

ただ、店舗数は人口などといった売り上げに直結するデータから導かれるのが普通で、人口密度が高くても人口が少なければ出店インセンティブにはならない。

人口と人口密度の関係

試しに人口を説明変数、人口密度を被説明変数として両者の関係を見てみると、驚くことに「人口が多いほど人口密度が高くなる（あるいはその逆）」という関係になる。

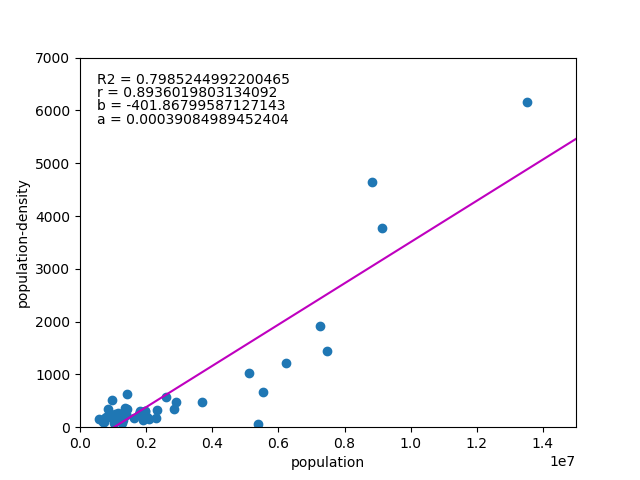
ここから先は人口論や地域論になりそうなので置いておくが、少なくとも日本においては、「狭いところほど人が集まっている傾向がある」ということになりそうである。

もちろんこれは他の国でも一般に当てはまることかもしれないが、朝のラッシュ時に特定の車両に無理やり乗り込んでいる割に離れた車両がすいているとか、1本電車を遅らせたらガラガラだったとか、そのあたりの行動パターンを見ていると、何となく日本に特有のような気がする。

道路延長との関係

最後に道路延長との関係を見てみる。

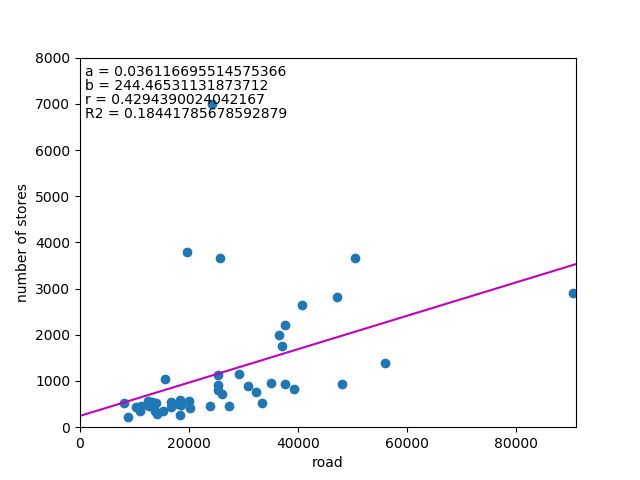
東京のように稠密な都市は例外とすると、概ね関係はありそうである。ただし相関係数、決定係数は高くない。

コンビニ店舗が道路の利便性に依っていることは推測できるが、やはり人口という売り上げ直結のデータに比べると関係は弱い。

高速道路の延長についても見てみたが、こちらはほとんど関係は見られなかった。

ただ、高速道路の延伸に伴ってコンビニエンスストアの店舗数が伸びているようであり、マクロな延長というよりも物流上のインパクトが大きいことは予想される。

相関係数

2019-09-29 / tau / コメントする

相関係数の定義

相関係数は、多数のデータの組がどの程度線形に近い性質を持つかを表す値で、以下で定義される。

(1) $\begin{eqnarray*} r &=& \frac{{\rm Cov}(X, Y)}{\sqrt{V(X) \cdot V(Y)}} \\ &=& \frac{E(X - \overline{X})(Y - \overline{Y})} {\sqrt{ ( E\left[ (X - \overline{X})^2 \right] E\left[ (Y - \overline{Y})^2 \right] }} \\ &=& \frac{\displaystyle \sum_{i=1}^{n}(x_i - \overline{x})(y_i - \overline{y})} {\left[ \displaystyle \sum_{i=1}^{n} (x_i - \overline{x})^2 \displaystyle \sum_{i=1}^{n} (y_i - \overline{y})^2 \right]^{1/2}} \end{eqnarray*}$

相関係数の線形変換

変数を線形変換した場合の相関係数は分散・共分散の性質から、以下のようになり、元のままか符号が反転する。

(2) $\begin{eqnarray*} r' &=& \frac{{\rm Cov}(aX+b, cY+d)}{\sqrt{V(aX+b) \cdot V(cY+d)}} \\ &=& \frac{ac{\rm Cov}(X, Y)}{\sqrt{a^2 V(X) \cdot c^2 V(Y)}} \\ &=& \frac{ac}{|ac|} \cdot r \end{eqnarray*}$

完全線形関係の場合の相関係数

XとYが完全な線形関係にある場合、相関係数は1または-1になる。このとき、傾きの大きさや、平行移動は相関係数に影響しない。

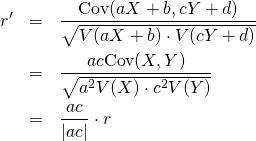
(3) $\begin{eqnarray*} r &=& \frac{ {\rm Cov}(X, aX+b) } { \left[ V(X) \cdot V(aX+b) \right]^{1/2} } \\ &=& \frac{ a {\rm Cov}(X, X) } { \left[ V(X) \cdot a^2 V(X) \right]^{1/2} } \\ &=& \frac{a}{\sqrt{a^2}} \cdot \frac{ {\rm Cov}(X, X) } { \left[ V(X) \cdot V(X) \right]^{1/2} } \\ &=& \frac{a}{|a|} \cdot \frac{ V(X) } { V(X) } \\ &=& 1 \; {\rm or} \; -1 \end{eqnarray*}$

いろいろな分布の相関係数

完全な線形関係

以下のコードで確認。

相関係数は傾きや平行移動に対して影響を受けず、増加関数なら1、減少関数なら－1になることがわかる。

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt

def cor(x, y):
    return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std()

x = np.linspace(0.2, 0.8, num=21)

y01 = np.array([x for x in x])
y02 = np.array([x * 0.5 for x in x])
y03 = np.array([x + 0.2 for x in x])
y04 = np.array([1 - x for x in x])

plt.axes().set_aspect('equal')
plt.xlim(0, 1)
plt.ylim(0, 1)

plt.scatter(x, y01, label='cor=' + str(cor(x, y01)))
plt.scatter(x, y02, label='cor=' + str(cor(x, y02)))
plt.scatter(x, y03, label='cor=' + str(cor(x, y03)))
plt.scatter(x, y04, label='cor=' + str(cor(x, y04)))

plt.legend()

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

def cor(x, y):

return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std()

x = np.linspace(0.2, 0.8, num=21)

y01 = np.array([x for x in x])

y02 = np.array([x * 0.5 for x in x])

y03 = np.array([x + 0.2 for x in x])

y04 = np.array([1 - x for x in x])

plt.axes().set_aspect('equal')

plt.xlim(0, 1)

plt.ylim(0, 1)

plt.scatter(x, y01, label='cor=' + str(cor(x, y01)))

plt.scatter(x, y02, label='cor=' + str(cor(x, y02)))

plt.scatter(x, y03, label='cor=' + str(cor(x, y03)))

plt.scatter(x, y04, label='cor=' + str(cor(x, y04)))

plt.legend()

plt.show()

線形性が強い関係

線形関数の値に対して、乱数でばらつきを与えた場合の相関係数の違いを示す。ばらつきが大きい方が相関係数は小さくなる。

y11 = np.array([x for x in x])
y12 = np.array([x + rnd.rand() * 0.2 * rnd.choice([-1, 1]) for x in x])
y13 = np.array([x + rnd.rand() * 0.4 * rnd.choice([-1, 1]) for x in x])

y11 = np.array([x for x in x])

y12 = np.array([x + rnd.rand() * 0.2 * rnd.choice([-1, 1]) for x in x])

y13 = np.array([x + rnd.rand() * 0.4 * rnd.choice([-1, 1]) for x in x])

負の線形性が強い場合は、相関係数がマイナスになる。

y21 = np.array([1 - x for x in x])
y22 = np.array([1 - x + rnd.rand()*0.2*rnd.choice([-1, 1]) for x in x])
y23 = np.array([1 - x + rnd.rand()*0.4*rnd.choice([-1, 1]) for x in x])

y21 = np.array([1 - x for x in x])

y22 = np.array([1 - x + rnd.rand()*0.2*rnd.choice([-1, 1]) for x in x])

y23 = np.array([1 - x + rnd.rand()*0.4*rnd.choice([-1, 1]) for x in x])

放物線（強い関係があるのに相関が低いケース）

以下のような放物線では、XとYにきちんとした数学的関係があるのに、相関係数がゼロに近くなる。

相関係数はXとYが単調増加／単調減少の度合いが強いほど、また線形関係に近いほど1に近くなるが、それ以外の関係が強い場合にはそれを補足できない場合がある。

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt

def cor(x, y):
    return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std()

x = np.linspace(0, 1.0, num=21)

y1 = np.array([4 * (x - 0.5)**2 for x in x])

plt.axes().set_aspect('equal')
plt.xlim(0, 1)
plt.ylim(0, 1)

plt.scatter(x, y1)

plt.text(0.05, 0.95, 'cor=' + str(cor(x, y1)))

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

def cor(x, y):

return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std()

x = np.linspace(0, 1.0, num=21)

y1 = np.array([4 * (x - 0.5)**2 for x in x])

plt.axes().set_aspect('equal')

plt.xlim(0, 1)

plt.ylim(0, 1)

plt.scatter(x, y1)

plt.text(0.05, 0.95, 'cor=' + str(cor(x, y1)))

plt.show()

反比例（負の線形性に見えてしまう場合）

以下は反比例関数の場合。

関数の形状や範囲に寄るが、この場合は相関係数の絶対値が0.8以上と1に近く、これだけ見ると負の線形性が強そうに見える。

x = np.linspace(0.1, 1.0, num=21)
y2 = np.array([0.1 / x for x in x])

1 2	x = np.linspace(0.1, 1.0, num=21) y2 = np.array([0.1 / x for x in x])

対数関数（正の線形性に見えてしまう場合）

対数関数の場合。この場合は0.9以上とかなり強い線形性を示唆している。

x = np.linspace(0.1, 1.0, num=21)
y3 = np.array([np.log(x*20-1)/4 for x in x])

1 2	x = np.linspace(0.1, 1.0, num=21) y3 = np.array([np.log(x*20-1)/4 for x in x])

相関係数に関する注意

本来の関係との乖離

先にみたように、線形関係ではないが数学的な関係を持つ場合に、相関係数からは全く関係がない、元の関係とは異なり線形関係を持つ、といった解釈になることがある。

相関係数が高い場合に、線形回帰式などで物事を予測する際には注意が必要。

変数間に解析的な関係が見いだせるならそれを重視すべきであり、よしんばそれがわからないにしても、定義域の範囲で「ある程度は当たる」程度に考えておくべきか。

因果関係

堂々と間違えられるケースが、「科学的な」記事やマスメディアなどでよくみられる。

相関係数は「変数間の単調な増加／減少傾向が強いかどうか」だけを示すもので、必ずしも因果関係を示唆しない。

気温が高いとビールはよく売れるがおでんは売れない。その二つに負の相関があるからといって、「ビール好きはおでんが嫌い」と言えないが、形を変えてこのような解釈がなされる恐れがある。

もともとのメカニズムで因果関係が示唆されていて、その上で相関係数の大きさを論じるなら意義もあるが、その場合でも、事象に対する寄与度などをよく考えておかないと「それだけが原因」と考えるような間違いを犯すことになる。

Python3 – 浮動小数点の誤差

2019-09-28 / tau / コメントする

概要

Pythonで浮動小数点誤差に行き当たった。

コンソール上にはErrorが表示され計算結果はnanになるが、配列を使っていたので、問題がどこで生じているかわかるまでにちょっと手間取った。

解析上の考え

中心が(cx, cy)、半径がrの円を考え、x座標を与えてそれに対する円上のy座標を計算しようとしていたとき。

このような円の方程式は、陰関数では以下のようになる。

$\begin{equation*} (x - c_x)^2 + (y - c_y)^2 = r^2 \end{equation*}$

これをy ≥ 0で解くと、

$\begin{equation*} y = c_y + \sqrt{r^2 - (x - c_x)^2} \end{equation*}$

問題の発生

中心の座標が(0.5, 0.5)、半径が0.3となるような円が欲しかったので、xの定義域を0.3～0.8として次のようなコードをPythonで書いた。実際はy < 0の部分も必要で、円周上だけでなく内部の座標をランダムに計算し、それらの相関係数を計算するというものだったが、本質的には変わらない。

import numpy as np

r = 0.3
cx, cy = 0.5, 0.5

x = np.linspace(0.3, 0.8, 11)
y = np.array([cy + np.sqrt(r**2 - (x - cx)**2)])

cor = np.sum((x - x.mean()) * (y - y.mean()) / x.std() / y.std())
print(cor)

import numpy as np

r = 0.3

cx, cy = 0.5, 0.5

x = np.linspace(0.3, 0.8, 11)

y = np.array([cy + np.sqrt(r**2 - (x - cx)**2)])

cor = np.sum((x - x.mean()) * (y - y.mean()) / x.std() / y.std())

print(cor)

その結果、cor=nanとなってしまう。実行時にsqrtの計算で警告が出ている。

C:\Users\tomo\Google �h���C�u\IT_and_Mobile\dev\python\trouble\float.py:7: RuntimeWarning: invalid value encountered in sqrt
  y = np.array([cy + np.sqrt(r**2 - (x - cx)**2)])
nan

C:\Users\tomo\Google �h��C�u\IT_and_Mobile\dev\python\trouble\float.py:7: RuntimeWarning: invalid value encountered in sqrt

y = np.array([cy + np.sqrt(r**2 - (x - cx)**2)])

nan

そこで配列x、yを表示させてみると、yの最後の要素がnanになっている。

print(x)
print(y)

1 2	print(x) print(y)

[0.3  0.35 0.4  0.45 0.5  0.55 0.6  0.65 0.7  0.75 0.8 ]
[[0.7236068  0.75980762 0.78284271 0.79580399 0.8        0.79580399
  0.78284271 0.75980762 0.7236068  0.66583124        nan]]

[0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 ]

[[0.7236068 0.75980762 0.78284271 0.79580399 0.8 0.79580399

0.78284271 0.75980762 0.7236068 0.66583124 nan]]

さらに、sqrtの中を表示させてみる。

for xx in x: print(r**2, (xx - cx)**2)

1	for xx in x: print(r2, (xx - cx)2)

0.09 0.04000000000000001
0.09 0.022500000000000006
0.09 0.009999999999999995
0.09 0.0024999999999999988
0.09 0.0
0.09 0.0025000000000000044
0.09 0.010000000000000018
0.09 0.022500000000000006
0.09 0.03999999999999998
0.09 0.0625
0.09 0.09000000000000002

0.09 0.04000000000000001

0.09 0.022500000000000006

0.09 0.009999999999999995

0.09 0.0024999999999999988

0.09 0.0

0.09 0.0025000000000000044

0.09 0.010000000000000018

0.09 0.022500000000000006

0.09 0.03999999999999998

0.09 0.0625

0.09 0.09000000000000002

最後のところで差し引かれる方の値がごくわずかに大きくなっていて、その結果根号の中が負の値となってnanが発生したらしい。

解決策

linspaceの範囲を円周上の上限・下限から少し内側にすることも考えられるが、今回はnumpy.around()を使った。

numpy.around(a, decimals=0)

これは値aを小数点以下decimalsの桁数で丸めてくれるもので、今回は小数点以下10桁目で丸めてみた。

import numpy as np

r = 0.3
cx, cy = 0.5, 0.5

x = np.linspace(0.3, 0.8, 11)
y = np.array([cy + np.sqrt(r**2 - np.around(x - cx, 10)**2)])

cor = np.sum((x - x.mean()) * (y - y.mean()) / x.std() / y.std())
print(cor)

import numpy as np

r = 0.3

cx, cy = 0.5, 0.5

x = np.linspace(0.3, 0.8, 11)

y = np.array([cy + np.sqrt(r**2 - np.around(x - cx, 10)**2)])

cor = np.sum((x - x.mean()) * (y - y.mean()) / x.std() / y.std())

print(cor)

この結果、正常に計算。

-6.625370822144879

1	-6.625370822144879

注意点

解析上値が等しくなる（差し引きゼロになる）ような場合でも、浮動小数点ではごくわずかな誤差のため、エラーとなることがある
numpy.linspace()を使うと上限・下限の間を等分してくれるのでありがたいが、上限・下限自体が他の値と厳密に等しくなければならない場合には、浮動小数点の誤差が生じるため注意が必要

matplotlib

2019-09-23 / tau / コメントする

pyplot～グラフの描画

patches～各種図形

pyplot.imshow()～画像表示

設定

markers
color
cmap～カラーマップ
linestyle

ヒストグラムと関数の重ね合わせ

Python3 – numpy

2019-09-23 / tau / コメントする

全般

numpyのインストール

randomモジュール

基本機能

配列・ndarray

Tips

配列の応用

集計・確率・統計

各種関数

`where()関数`

Numpy.where()は、配列中の要素を検索してそのインデックスを得たり、配列の条件によって指定した配列から要素を選び出すことができる。

numpy – 統計量と組み込み関数の注意点

2019-09-22 / tau / コメントする

概要

Pythonのnumpyで統計量を扱う場合、分散・共分散で注意を要する点がある。Excelの関数でも同様だが、分散・共分散が標本値からそのまま計算した値か、不偏推定量として計算した値か、ということを意識する必要がある。

ここでは、ndarrayから律義に計算した値と、numpyの組み込み関数から計算した値を比較してみる。

標本数・総和・平均

標本として与えた配列の要素数、全要素の和、総和を要素数で除した値で、そのまま母集団の不偏推定量。

import numpy as np

x = np.array([1, 2, 3, 4, 5])
n = len(x)
sum_x = x.sum()
mean_x = sum_x / n
print(n)
print(sum_x)
print(mean_x, x.mean())

# 5
# 15
# 3.0 3.0

import numpy as np

x = np.array([1, 2, 3, 4, 5])

n = len(x)

sum_x = x.sum()

mean_x = sum_x / n

print(n)

print(sum_x)

print(mean_x, x.mean())

# 5

# 15

# 3.0 3.0

分散・標準偏差の食い違い

`var()`、`std()`は標本の分散・標準偏差

分散・共分散については、提供されたメソッドvar()、std()は標本数で除した標本分散・共分散となる。

x = np.array([1, 2, 3, 4, 5])
n = len(x)
var_x = np.sum((x - x.mean())**2) / n
std_x = np.sqrt(var_x)
print(var_x, x.var())
print(std_x, x.std())

# 2.0 2.0
# 1.4142135623730951 1.4142135623730951

x = np.array([1, 2, 3, 4, 5])

n = len(x)

var_x = np.sum((x - x.mean())**2) / n

std_x = np.sqrt(var_x)

print(var_x, x.var())

print(std_x, x.std())

# 2.0 2.0

# 1.4142135623730951 1.4142135623730951

不偏分散やその平方根を求める場合は、var()、std()の引数でddof=1とする。

`cov()`で与えられるのは不偏推定量

numpy.cov()で二つの一次元配列の分散・共分散行列を得ることができる。分散共分散行列は

$\begin{equation*} \left[ \begin{array}{ll} {\rm Var}(X) & {\rm Cov}(XY) \\ {\rm Cov}(XY) & {\rm Var}(Y) \end{array} \right] \end{equation*}$

で定義されるが、以下の計算結果の対角要素は、先の分散の計算結果(2.0)と異なっている。

x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 2, 3, 4, 5])
print(np.cov(x, y))

# [[2.5 2.5]
#  [2.5 2.5]]

x = np.array([1, 2, 3, 4, 5])

y = np.array([1, 2, 3, 4, 5])

print(np.cov(x, y))

# [[2.5 2.5]

# [2.5 2.5]]

これらの値は、分散を標本分散ではなく不偏推定量で計算しているためで、試しに先の計算を不偏分散で計算してみると結果は整合する。

ちなみに標本分散は偏差の二乗和を標本数nで割り、不偏分散はn-1で割る。

x = np.array([1, 2, 3, 4, 5])
n = len(x)
var_x = np.sum((x - x.mean())**2) / (n - 1)
print(var_x)

# 2.5

x = np.array([1, 2, 3, 4, 5])

n = len(x)

var_x = np.sum((x - x.mean())**2) / (n - 1)

print(var_x)

# 2.5

共分散にも注意

上記では分散について確認したが、共分散についても注意が必要。

共分散は一般に以下で定義される。

$\begin{equation*} {\rm Cov}(X, Y) = E((X - \overline{X}) (Y - \overline{Y})) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \overline{x}) (y_i - \overline{y}) \end{equation*}$

これに従って計算した結果。

x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 2, 3, 4, 5])
n = len(x)
cov_xy = np.sum((x - x.mean())*(y - y.mean())) / n
print(cov_xy)

# 2.0

x = np.array([1, 2, 3, 4, 5])

y = np.array([1, 2, 3, 4, 5])

n = len(x)

cov_xy = np.sum((x - x.mean())*(y - y.mean())) / n

print(cov_xy)

# 2.0

この結果は、numpy.cov()で計算した非対角要素2.5と食い違う。

ここでn→n-1として計算しなおすと結果は2.5となり同じ値となる。

共分散用は、たとえば回帰分析の残差変動を計算するときに利用するが、その時には標本の共分散を使うので、注意が必要。

numpyで統計計算をする際、特に共分散については、律義に定義式から計算するのがよさそう。

numpy – 配列の統計計算（二次元配列）

2019-09-22 / tau / コメントする

概要

二次元配列についても、一次元配列と同様な統計関係のメソッド群がある。

二次元についても、同じ機能のメソッドがnumpy、ndarrayのメソッドとして準備されている。

二次元配列の場合は、最小・総和・平均などの計算を全要素／列単位／行単位のいずれで行うかを区別する。具体例として、以下の3×3配列の最小値min()を全要素、列単位、行単位で計算した例を示す。

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(np.min(m))
print(np.min(m, axis=0))
print(np.min(m, axis=1))

# 1
# [1 2 3]
# [1 4 7]

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(np.min(m))

print(np.min(m, axis=0))

print(np.min(m, axis=1))

# 1

# [1 2 3]

# [1 4 7]

引数axisを指定しないと全要素が対象となり、axis=0を指定すると列ごとの計算結果を一次元の配列に、axis=1を指定すると行ごとの計算結果を一次元の配列にして返す。

axis=1の場合、計算は行ごとに行われるが、結果は列ベクトルではなく行ベクトルの配列となる。

また、numpyのメソッドではなくndarrayのメソッドでも同じように使える。

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(m.min())
print(m.min(axis=0))
print(m.min(axis=1))

# 1
# [1 2 3]
# [1 4 7]

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(m.min())

print(m.min(axis=0))

print(m.min(axis=1))

# 1

# [1 2 3]

# [1 4 7]

最小値・最大値

最小値／最大値を返す。

numpy.min(m, axis=0/1)
numpy.max(m, axis=0/1)
m.min(axis=0/1)
m.max(axis=0/1)

結果は同じなので、numpyのメソッドについて実行例を示す。

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.min(m))         # 1
print(np.min(m, axis=0)) # [1 2 3]
print(np.min(m, axis=1)) # [1 4 7]
print(np.max(m))         # 9
print(np.max(m, axis=0)) # [7 8 9]
print(np.max(m, axis=1)) # [3 6 9]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.min(m)) # 1

print(np.min(m, axis=0)) # [1 2 3]

print(np.min(m, axis=1)) # [1 4 7]

print(np.max(m)) # 9

print(np.max(m, axis=0)) # [7 8 9]

print(np.max(m, axis=1)) # [3 6 9]

総和・総積

一次元配列の全要素の和・積を返す。

numpy.sum(m, axis=0/1)
numpy.prod(m, axis=0/1)
m.sum(axis=0/1)
m.prod(axis=0/1)

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.sum(m))          # 45
print(np.sum(m, axis=0))  # [12 15 18]
print(np.sum(m, axis=1))  # [ 6 15 24]
print(np.prod(m))         # 362880
print(np.prod(m, axis=0)) # [ 28  80 162]
print(np.prod(m, axis=1)) # [  6 120 504]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.sum(m)) # 45

print(np.sum(m, axis=0)) # [12 15 18]

print(np.sum(m, axis=1)) # [ 6 15 24]

print(np.prod(m)) # 362880

print(np.prod(m, axis=0)) # [ 28 80 162]

print(np.prod(m, axis=1)) # [ 6 120 504]

平均・分散・標準偏差

一次元配列の要素の平均、分散、標準偏差を返す。分散は標本分散なので、不偏分散が必要な場合はvar()*n/(n-1)とする（ただしn=len(v)）。

numpy.mean(m, axis=0/1)
numpy.var(m, axis=0/1)
numpy.std(m, axis=0/1)
m.mean(axis=0/1)
m.var(axis=0/1)
m.std(axis=0/1)

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.mean(m))         # 5.0
print(np.mean(m, axis=0)) # [4. 5. 6.]
print(np.mean(m, axis=1)) # [2. 5. 8.]
print(np.var(m))          # 6.666666666666667
print(np.var(m, axis=0))  # [6. 6. 6.]
print(np.var(m, axis=1))  # [0.66666667 0.66666667 0.66666667]
print(np.std(m))          # 2.581988897471611
print(np.std(m, axis=0))  # [2.44948974 2.44948974 2.44948974]
print(np.std(m, axis=1))  # [0.81649658 0.81649658 0.81649658]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.mean(m)) # 5.0

print(np.mean(m, axis=0)) # [4. 5. 6.]

print(np.mean(m, axis=1)) # [2. 5. 8.]

print(np.var(m)) # 6.666666666666667

print(np.var(m, axis=0)) # [6. 6. 6.]

print(np.var(m, axis=1)) # [0.66666667 0.66666667 0.66666667]

print(np.std(m)) # 2.581988897471611

print(np.std(m, axis=0)) # [2.44948974 2.44948974 2.44948974]

print(np.std(m, axis=1)) # [0.81649658 0.81649658 0.81649658]

累積和・累積積

一次元配列の要素について先頭から累積して積・和を計算し、それらを要素とする配列を返す。

二次元配列でaxis=0を指定した場合、列ごとに行方向に累積した値が並べられた二次元配列となり、axis=1を指定した場合は行ごとに列方向に累積した値が並べられた二次元配列となる。

numpy.cumsum(m)
numpy.cumprod(m)
m.cumsum()
m.cumprod()

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.cumsum(m))
print(np.cumsum(m, axis=0))
print(np.cumsum(m, axis=1))
print(np.cumprod(m))
print(np.cumprod(m, axis=0))
print(np.cumprod(m, axis=1))

# [ 1  3  6 10 15 21 28 36 45]
# [[ 1  2  3]
#  [ 5  7  9]
#  [12 15 18]]
# [[ 1  3  6]
#  [ 4  9 15]
#  [ 7 15 24]]

# [     1      2      6     24    120    720   5040  40320 362880]
# [[  1   2   3]
#  [  4  10  18]
#  [ 28  80 162]]
# [[  1   2   6]
#  [  4  20 120]
#  [  7  56 504]]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.cumsum(m))

print(np.cumsum(m, axis=0))

print(np.cumsum(m, axis=1))

print(np.cumprod(m))

print(np.cumprod(m, axis=0))

print(np.cumprod(m, axis=1))

# [ 1 3 6 10 15 21 28 36 45]

# [[ 1 2 3]

# [ 5 7 9]

# [12 15 18]]

# [[ 1 3 6]

# [ 4 9 15]

# [ 7 15 24]]

# [ 1 2 6 24 120 720 5040 40320 362880]

# [[ 1 2 3]

# [ 4 10 18]

# [ 28 80 162]]

# [[ 1 2 6]

# [ 4 20 120]

# [ 7 56 504]]

numpy – 配列の統計計算（一次元配列）

2019-09-22 / tau / コメントする

概要

一次元配列について、様々な統計関係の計算をするメソッド群。

同じ機能のメソッドがnumpy、ndarrayのメソッドとして準備されている。例えば一次元配列vについて最小値を求めるメソッドは、numpy.min(v)とv.min()のいずれも同じ結果を返す。

最小値・最大値

一次元配列の要素のうち最小値／最大値を返す。

numpy.min(v)
numpy.max(v)
v.min()
v.max()

結果は同じなので、numpyのメソッドについて実行例を示す。

v = np.array([1, 2, 3, 4])
print(np.min(v))
print(np.max(v))

# 1
# 4

v = np.array([1, 2, 3, 4])

print(np.min(v))

print(np.max(v))

# 1

# 4

総和・総積

一次元配列の全要素の和・積を返す。

numpy.sum(v)
numpy.prod(v)
v.sum()
v.prod()

v = np.array([1, 2, 3, 4])
print(np.sum(v))
print(np.prod(v))

# 10
# 24

v = np.array([1, 2, 3, 4])

print(np.sum(v))

print(np.prod(v))

# 10

# 24

平均・分散・標準偏差

一次元配列の要素の平均、分散、標準偏差を返す。分散は標本分散なので、不偏分散が必要な場合はvar()*n/(n-1)とする（ただしn=len(v)）。

numpy.mean(v)
numpy.var(v)
numpy.std(v)
v.mean()
v.var()
v.std()

v = np.array([1, 2, 3, 4])
print(np.mean(v))
print(np.var(v))
print(np.std(v))

# 2.5
# 1.25
# 1.118033988749895

v = np.array([1, 2, 3, 4])

print(np.mean(v))

print(np.var(v))

print(np.std(v))

# 2.5

# 1.25

# 1.118033988749895

$\begin{eqnarray*} \overline{V} &=& \frac{1 + 2 + 3 + 4}{4} = 2.5 \\ {\rm Var}(V) &=& \frac{(1-2.5)^2+(2-2.5)^2+(3-2.5)^2+(4-2.5)^2}{4} \\ &=& \frac{2.25+0.25+0.25+2.25}{4} = \frac{5}{4} \\ &=& 1.25 \\ \sigma_V &=& \sqrt{1.25} = 1.1180 \ldots \end{eqnarray*}$

累積和・累積積

一次元配列の要素について先頭から累積して積・和を計算し、それらを要素とする配列を返す。

numpy.cumsum(v)
numpy.cumprod(v)
v.cumsum()
v.cumprod()

v = np.array([1, 2, 3, 4])
print(np.cumsum(v))
print(np.cumprod(v))

# [ 1  3  6 10]
# [ 1  2  6 24]

v = np.array([1, 2, 3, 4])

print(np.cumsum(v))

print(np.cumprod(v))

# [ 1 3 6 10]

# [ 1 2 6 24]

numpy – 配列要素の演算

2019-09-17 / tau / コメントする

要素に対するスカラー演算

配列の要素に対するスカラー演算は、それぞれの要素に作用。

v = np.array([1, 2, 3])
print(v + 1)
print(v - 1)
print(v * 2)
print(v / 2)

# [2 3 4]
# [0 1 2]
# [2 4 6]
# [0.5 1.  1.5]

v = np.array([1, 2, 3])

print(v + 1)

print(v - 1)

print(v * 2)

print(v / 2)

# [2 3 4]

# [0 1 2]

# [2 4 6]

# [0.5 1. 1.5]

二次元配列も同じ。

m = np.array([[1, 2, 3], [4, 5, 6]])
print(m1 + 1)
print(m1 - 1)
print(m1 * 2)
print(m1 / 2)

# [[2 3 4]
#  [5 6 7]]
# [[0 1 2]
#  [3 4 5]]
# [[ 2  4  6]
#  [ 8 10 12]]
# [[0.5 1.  1.5]
#  [2.  2.5 3. ]]

m = np.array([[1, 2, 3], [4, 5, 6]])

print(m1 + 1)

print(m1 - 1)

print(m1 * 2)

print(m1 / 2)

# [[2 3 4]

# [5 6 7]]

# [[0 1 2]

# [3 4 5]]

# [[ 2 4 6]

# [ 8 10 12]]

# [[0.5 1. 1.5]

# [2. 2.5 3. ]]

なお、配列が後ろに来ても要素ごとに演算。

v = np.array([1, 2, 3])
print(1 - v)
print(2 / v)

# [ 0 -1 -2]
# [2.         1.         0.66666667]

v = np.array([1, 2, 3])

print(1 - v)

print(2 / v)

# [ 0 -1 -2]

# [2. 1. 0.66666667]

要素ごとの演算

同じ形状の配列同士の演算は、それぞれの要素ごとの演算。

v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
print(v2 + v1)
print(v2 - v1)
print(v2 * v1)
print(v2 / v1)

# [5 7 9]
# [3 3 3]
# [ 4 10 18]
# [4.  2.5 2. ]

v1 = np.array([1, 2, 3])

v2 = np.array([4, 5, 6])

print(v2 + v1)

print(v2 - v1)

print(v2 * v1)

print(v2 / v1)

# [5 7 9]

# [3 3 3]

# [ 4 10 18]

# [4. 2.5 2. ]

要素ごとの比較

配列同士の比較は、要素ごとの比較結果の配列。

v1 = np.array([0, 1, 2, 3])
v2 = np.array([0, 2, 2, 0])
print(v1 == v2)
print(v1 > v2)

# [ True False  True False]
# [False False False  True]

v1 = np.array([0, 1, 2, 3])

v2 = np.array([0, 2, 2, 0])

print(v1 == v2)

print(v1 > v2)

# [ True False True False]

# [False False False True]

関数演算

numpyの関数の引数が配列の場合、要素ごとの演算結果となる。

v = np.array([1, 2, 3])
print(np.sqrt(v))
print(np.log(v))

# [1.         1.41421356 1.73205081]
# [0.         0.69314718 1.09861229]

v = np.array([1, 2, 3])

print(np.sqrt(v))

print(np.log(v))

# [1. 1.41421356 1.73205081]

# [0. 0.69314718 1.09861229]

numpy – ファイルの保存と読み込み

2019-09-10 / tau / コメントする

バイナリファイル

バイナリファイルとしての保存にはnp.save()、その読み込みにはnp.load()を使う。基本的なオプションは以下の通り。

numpy.save("ファイル名", 配列)
配列 = numpy.load("ファイル名")

注意点として、ファイルの拡張子は.npy固定。

saveのファイル名に拡張子をつけない場合、自動的に拡張子.npyが付加される
saveのファイル名に別の拡張子を書いても、その後ろに.npyが付加される
loadのファイル名の拡張子は.npyでなければならない（違う場合はFileNotFoundError）

import numpy as np

a1 = np.array([0, 1, 2, 3])
a2 = np.array([[0, 1, 2], [3, 4, 5]])

np.save("bin-1d", a1)
np.save("bin-2d", a2)

b1 = np.load("bin-1d.npy")
b2 = np.load("bin-2d.npy")

print(b1)
print(b2)

# [0 1 2 3]
# [[0 1 2]
#  [3 4 5]]

import numpy as np

a1 = np.array([0, 1, 2, 3])

a2 = np.array([[0, 1, 2], [3, 4, 5]])

np.save("bin-1d", a1)

np.save("bin-2d", a2)

b1 = np.load("bin-1d.npy")

b2 = np.load("bin-2d.npy")

print(b1)

print(b2)

# [0 1 2 3]

# [[0 1 2]

# [3 4 5]]

テキストファイル

概要

テキストファイルとしての保存にはnp.savetxt()、その読み込みにはnp.loadtxt()を使う。扱える配列の次元は1次元か2次元のみ。基本的なオプションは以下の通り。

numpy.savetxt( fname, # ファイル名を任意の拡張子まで指定 X, # 書き込む配列 fmt='%.18e', # 書き込む書式 delimiter=' ', # 行内の数値の区切り newline='n', # 改行文字 header='', # ヘッダー文字列 footer='', # フッター文字列 comments='# ', # コメントの開始文字 encoding=None # エンコーディング )
numpy.loadtxt( fname, # ファイル名（拡張子まで） dtype=<class 'float'>, # データの型 comments='#', # コメント開始文字 delimiter=None, # 区切り文字（デフォルトはスペース） converters=None, skiprows=0, # ファイル先頭から指定した行数だけ読み飛ばす usecols=None, # タプルで指定した列のみ読み込み unpack=False, ndmin=0, encoding='bytes', max_rows=None)

なお、numpy.ndarrayはすべての要素の型が同じでなければならず、リストやタプルのように要素の型を混在させることはできない。

数値データ

数値データのみを扱う場合、整数でも自動的に実数型に変換されて読み込まれる。

実行例

import numpy as np

a1 = np.array([0, 1, 2, 3])
a2 = np.array([[0, 1, 2], [3, 4, 5]])

np.savetxt("bin-1d.txt", a1)
np.savetxt("bin-2d.txt", a2)

b1 = np.loadtxt("bin-1d.txt")
b2 = np.loadtxt("bin-2d.txt")

print(b1)
print(b2)

# [0. 1. 2. 3.]
# [[0. 1. 2.]
# [3. 4. 5.]]

import numpy as np

a1 = np.array([0, 1, 2, 3])

a2 = np.array([[0, 1, 2], [3, 4, 5]])

np.savetxt("bin-1d.txt", a1)

np.savetxt("bin-2d.txt", a2)

b1 = np.loadtxt("bin-1d.txt")

b2 = np.loadtxt("bin-2d.txt")

print(b1)

print(b2)

# [0. 1. 2. 3.]

# [[0. 1. 2.]

# [3. 4. 5.]]

このときのファイルの内容は以下のようになっている。

...\python>type bin-1d.txt
0.000000000000000000e+00
1.000000000000000000e+00
2.000000000000000000e+00
3.000000000000000000e+00

...\python>type bin-2d.txt
0.000000000000000000e+00 1.000000000000000000e+00 2.000000000000000000e+00
3.000000000000000000e+00 4.000000000000000000e+00 5.000000000000000000e+00

...\python>type bin-1d.txt

0.000000000000000000e+00

1.000000000000000000e+00

2.000000000000000000e+00

3.000000000000000000e+00

...\python>type bin-2d.txt

0.000000000000000000e+00 1.000000000000000000e+00 2.000000000000000000e+00

3.000000000000000000e+00 4.000000000000000000e+00 5.000000000000000000e+00

3次元以上の配列を書き込もうとするとエラー。

  File "C:...\Python\Python37-32\lib\site-packages\numpy\lib\npyio.py", line 1382, in savetxt
    "Expected 1D or 2D array, got %dD array instead" % X.ndim)
ValueError: Expected 1D or 2D array, got 3D array instead

File "C:...\Python\Python37-32\lib\site-packages\numpy\lib\npyio.py", line 1382, in savetxt

"Expected 1D or 2D array, got %dD array instead" % X.ndim)

ValueError: Expected 1D or 2D array, got 3D array instead

文字列

文字列データについては、書き込む場合はfmt="%s"、読み込む場合にはdtype="unicode"を指定。

import numpy as np

a3 = np.array(['北海道', '本州', '四国', '九州'])
print(a3)

np.savetxt("text.txt", a3, fmt="%s")

b3 = np.loadtxt("text.txt", dtype="unicode")

print(b3)

# ['北海道' '本州' '四国' '九州']
# ['北海道' '本州' '四国' '九州']

import numpy as np

a3 = np.array(['北海道', '本州', '四国', '九州'])

print(a3)

np.savetxt("text.txt", a3, fmt="%s")

b3 = np.loadtxt("text.txt", dtype="unicode")

print(b3)

# ['北海道' '本州' '四国' '九州']

このとき、text.txtファイルの中は以下のようになっている。

北海道
本州
四国
九州

北海道

本州

四国

九州

CSVファイルの読み込み

以下のようなCSVファイルを配列に読み込む。

,店舗数,国調人口
,2016,2015
北海道,2906,5381733
青森県,573,1308265
岩手県,523,1279594
・・・・・

,店舗数,国調人口

,2016,2015

北海道,2906,5381733

青森県,573,1308265

岩手県,523,1279594

・・・・・

numpy.arrayはすべての要素の型が同じである必要があるため、上記のように文字列と数値が混在したファイルを一つの配列に読み込もうとするとエラーになる。

data = np.loadtxt('conv-pop.csv', delimiter=',', skiprows=2)

# ValueError: could not convert string to float: '北海道'

data = np.loadtxt('conv-pop.csv', delimiter=',', skiprows=2)

# ValueError: could not convert string to float: '北海道'

都道府県名と2次元のデータを別々に読み込むことは可能。

title = np.loadtxt(
    'conv-pop.csv', dtype='unicode', delimiter=',', skiprows=2, usecols=(0))
data = np.loadtxt('conv-pop.csv', delimiter=',', skiprows=2, usecols=(1,2))
print(title)
print(data)

# ['北海道' '青森県' '岩手県' '宮城県' '秋田県' '山形県' '福島県' '茨城県' '栃木県' '群馬県' '埼玉県' '千葉県'
#  '東京都' '神奈川県' '新潟県' '富山県' '石川県' '福井県' '山梨県' '長野県' '岐阜県' '静岡県' '愛知県' '三重県'
#  '滋賀県' '京都府' '大阪府' '兵庫県' '奈良県' '和歌山県' '鳥取県' '島根県' '岡山県' '広島県' '山口県' '徳島県'
#  '香川県' '愛媛県' '高知県' '福岡県' '佐賀県' '長崎県' '熊本県' '大分県' '宮崎県' '鹿児島県' '沖縄県']
# [[2.9060000e+03 5.3817330e+06]
#  [5.7300000e+02 1.3082650e+06]
#  [5.2300000e+02 1.2795940e+06]
・・・・・

title = np.loadtxt(

'conv-pop.csv', dtype='unicode', delimiter=',', skiprows=2, usecols=(0))

data = np.loadtxt('conv-pop.csv', delimiter=',', skiprows=2, usecols=(1,2))

print(title)

print(data)

# ['北海道' '青森県' '岩手県' '宮城県' '秋田県' '山形県' '福島県' '茨城県' '栃木県' '群馬県' '埼玉県' '千葉県'

# '東京都' '神奈川県' '新潟県' '富山県' '石川県' '福井県' '山梨県' '長野県' '岐阜県' '静岡県' '愛知県' '三重県'

# '滋賀県' '京都府' '大阪府' '兵庫県' '奈良県' '和歌山県' '鳥取県' '島根県' '岡山県' '広島県' '山口県' '徳島県'

# '香川県' '愛媛県' '高知県' '福岡県' '佐賀県' '長崎県' '熊本県' '大分県' '宮崎県' '鹿児島県' '沖縄県']

# [[2.9060000e+03 5.3817330e+06]

# [5.7300000e+02 1.3082650e+06]

# [5.2300000e+02 1.2795940e+06]

・・・・・

読み込み時にUnicodeエラーが出た場合

ファイル読み込み時に以下のようなエラーが出た場合。

UnicodeDecodeError: 'cp932' codec can't decode byte 0xef in position 0: illegal multibyte sequence

1	UnicodeDecodeError: 'cp932' codec can't decode byte 0xef in position 0: illegal multibyte sequence

引数にencoding='utf8'を指定して回避。

その他のメソッド

savez()/load(): 複数のファイルを非圧縮で扱う。
savez_compressed()/load(): 複数のファイルを圧縮して扱う
ndarray.tofile(): 配列のストレージへの書き込み。

概要

人口との関係

面積との関係

店舗数と面積の関係

人口密度

人口と人口密度の関係

道路延長との関係

相関係数の定義

相関係数の線形変換

完全線形関係の場合の相関係数

いろいろな分布の相関係数

完全な線形関係

線形性が強い関係

放物線（強い関係があるのに相関が低いケース）

反比例（負の線形性に見えてしまう場合）

対数関数（正の線形性に見えてしまう場合）

相関係数に関する注意

本来の関係との乖離

因果関係

概要

解析上の考え

問題の発生

解決策

注意点

全般

基本機能

配列・ndarray

集計・確率・統計

各種関数

where()関数

概要

標本数・総和・平均

分散・標準偏差の食い違い

var()、std()は標本の分散・標準偏差

cov()で与えられるのは不偏推定量

共分散にも注意

概要

最小値・最大値

総和・総積

平均・分散・標準偏差

累積和・累積積

概要

最小値・最大値

総和・総積

平均・分散・標準偏差

累積和・累積積

要素に対するスカラー演算

要素ごとの演算

要素ごとの比較

関数演算

バイナリファイル

テキストファイル

概要

数値データ

文字列

CSVファイルの読み込み

読み込み時にUnicodeエラーが出た場合

その他のメソッド

`where()関数`

`var()`、`std()`は標本の分散・標準偏差

`cov()`で与えられるのは不偏推定量