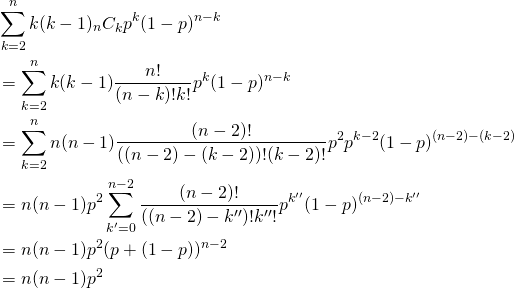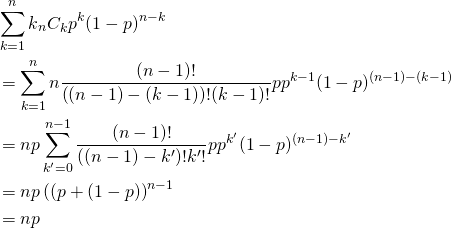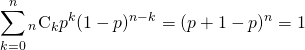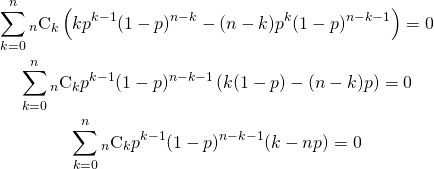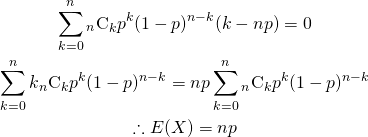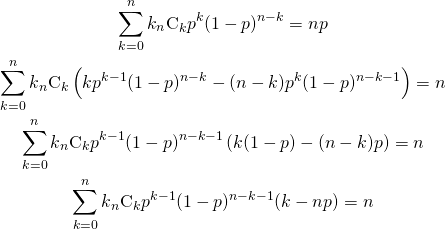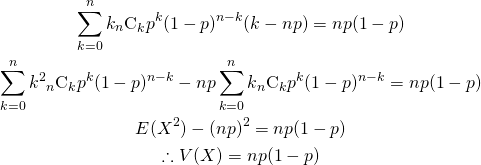やりたいこと
たとえば多数の計算結果を表示するとき、リストなら最初だけ"["がついて、各要素の後ろに", "が付加されて、最後の要素だけそのカンマがなくて"]"が表示される。このような処理をいろいろな形で実装したいというような場合。
単純に考えると次のように格好が悪い。
|
1 2 3 4 5 6 7 8 |
lst = [10, 20, 30, 40] print("<", end="") for e in lst: print("{}, ".format(e), end="") print(">") # <10, 20, 30, 40, > |
これを、<0, 1, 2, 3, 4>のように末尾だけ表示方法を変えたい、さらには、何個かごとに改行させて、2行目以降の行頭を1行目と変更したいときの処理を考える。
インデックスを利用する方法
1行で表示する場合
以下の例では、enumerateでコレクションのインデックスを取り出して、その値によって処理を分けている。行頭"<"の処理はforループの前でやってもよいが、次の複数行表示の準備としてif文で判定している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
for i, e in enumerate(lst): # 1文字目の場合、要素表示に先立って"<"を表示 if i == 0: print("<", end="") # 要素を表示 print(e, end="") # 最終要素の場合は">"、そうでなければ", "を表示 if i == len(lst) - 1: print(">") else: print(", ", end="") # <10, 20, 30, 40> |
複数行に分けて表示する場合
長いリストや多次元の配列などを複数行に分けて表示したい場合、行ごとの行末文字も変わってくる。そのような処理をforループで書いてみた。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
lst = [2, 4, 6, 8, 10, 12, 14, 16] num_in_line = 3 for i, e in enumerate(lst): # 1行目の場合行頭文字は"<"、そうでなければ" "で段下げ prefix = "<" if i // num_in_line == 0 else " " # 要素の後に表示する文字を、最後の文字だけ">"、その他の場合は", "とする suffix = ">" if i == len(lst) - 1 else ", " # 1文字目の場合、要素表示に先立ってprefixを表示 if i % num_in_line == 0: print(prefix, end="") # 要素とsuffixを表示 print("{:2d}{}".format(e, suffix), end="") # 行末要素か最終要素の場合は改行 if i % num_in_line == num_in_line - 1 or i == len(lst) - 1: print() # < 2, 4, 6, # 8, 10, 12, # 14, 16> |
ジェネレーターを使う方法
ジェネレーターを使った方法。このジェネレーターは、各要素のprefix、本体要素、suffixの3つを返す。
1文字目だけ処理を変えるため、コレクションをイテレーターとし、ループに入る前に最初の要素を取り出している。next()関数でイテレーターの内容を取り出すと、その後のforループでは以降の要素が順次取り出されることを利用している。
prefixは最初だけ"<"を使い、その後は""としてprefixなしとして扱っている。
1行で表示する場合
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
lst = [10, 20, 30, 40] def generator(lst): # 先頭に表示させる文字 prefix = "<" # 与えられたコレクションをイテレーターとする it = iter(lst) # まず最初の要素を取得しておく next_element = next(it) # 最初の要素は既に取得されているので、current_elementは2つ目の要素から # 取得される for current_element in it: # ジェネレーターはprefix、本体要素、suffixを返す yield prefix, next_element, ", " # 以下、取得した要素をnext_elementに順次移していく next_element = current_element # 2つ目の要素以降はprefixなし prefix = "" # 最後の要素のみsuffixを">"にする yield prefix, next_element, ">" for prefix, e, suffix in generator(lst): print("{}{}{}".format(prefix, e, suffix), end="") print() # <10, 20, 30, 40> |
複数行に分けて表示する場合
複数行に分ける場合、1行当たりの要素数を設定し、カウンターで要素位置を検出している。カウンターの値から先頭要素と判定した場合にprefixを" "とし、その他の場合は""としている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
lst = [2, 4, 6, 8, 10, 12, 14, 16] def generator(lst): num_in_line = 3 prefix = "<" it = iter(lst) next_element = next(it) # 行内の要素位置用のカウンター counter = 0 for current_element in it: # counterは1~最大要素数でサイクリックに変化させる counter += 1 # 行内の最終位置の要素なら改行、そうでなければ継続 if counter == num_in_line: suffix = ",\n" counter = 0 else: suffix = ", " yield prefix, next_element, suffix next_element = current_element # 2行目以降の先頭ならprefixを" "とする prefix = " " if counter == 0 else "" yield prefix, next_element, ">" for prefix, e, suffix in generator(lst): print("{}{:2d}{}".format(prefix, e, suffix), end="") print() # < 2, 4, 6, # 8, 10, 12, # 14, 16> |
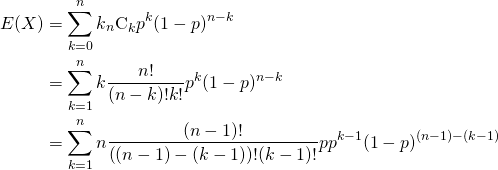
![Rendered by QuickLaTeX.com \begin{alignat*}{1} V(X) &= E(X^2) - [E(X)]^2 \\ &= \sum_{k=0}^n k^2 {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=0}^n \left( k(k-1) + k \right) {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=2}^n k(k-1) {}_n C_k p^k (1-p)^{n-k} + \sum_{k=1}^n k {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ \end{alignat*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-443e6acf6b414d16761dcd5f2a012a8d_l3.png)