Python – file

2020-03-30 / tau / コメントする

osパッケージのgetcwd()を使ってカレントディレクトリーを取得しようとして、Atomからの直接実行などのときにうまくいかなかった。

このような場合、__file__で実行ファイルの位置を得ることができる。また、os.path.dirname(__file__)でファイル名を除いたパスを、os.path.basename(__file__)でファイル名のみを得ることができる。

実行方法によってはエラーとなる。

import os

print("__file__:{}".format(__file__))
print("dirname :{}".format(os.path.dirname(__file__)))
print("basename:{}".format(os.path.basename(__file__)))
print("files   :{}".format(os.listdir(os.path.dirname(__file__))))

import os

print("__file__:{}".format(__file__))

print("dirname :{}".format(os.path.dirname(__file__)))

print("basename:{}".format(os.path.basename(__file__)))

print("files :{}".format(os.listdir(os.path.dirname(__file__))))

Atomから実行した場合

__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

コマンドラインから実行ファイル(__file__.py)のあるディレクトリーに移動し、直接ファイル名をタイプした場合

C:\Users\...\dev\python\packages\os>__file__.py
__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

C:\Users\...\dev\python\packages\os>__file__.py

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

コマンドラインから実行ファイル(__file__.py)のあるディレクトリーに移動し、”python 実行ファイル名”で実行した場合

C:\Users\tomo\...\dev\python\packages\os>python __file__.py
__file__:__file__.py
dirname :
basename:__file__.py
Traceback (most recent call last):
  File "__file__.py", line 6, in <module>
    print("files   :{}".format(os.listdir(os.path.dirname(__file__))))
FileNotFoundError: [WinError 3] 指定されたパスが見つかりません。: ''

C:\Users\tomo\...\dev\python\packages\os>python __file__.py

__file__:__file__.py

dirname :

basename:__file__.py

Traceback (most recent call last):

File "__file__.py", line 6, in <module>

print("files :{}".format(os.listdir(os.path.dirname(__file__))))

FileNotFoundError: [WinError 3] 指定されたパスが見つかりません。: ''

上記と同じだが、実行ファイル名を相対パスで指定した場合

C:\Users\...\dev\python\packages\os>python ./__file__.py
__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

C:\Users\...\dev\python\packages\os>python ./__file__.py

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

Boston house pricesデータセットの俯瞰

2020-03-28 / tau / コメントする

概要

Boston house pricesデータセットは、持家の価格とその持家が属する地域に関する指標からなるデータセットで、多変量の特徴量から属性値を予想するモデルに使われる。

各特徴量の分布

データセットからBostonにおける506の地域における13の特徴量と住宅価格の中央値が得られるが、それぞれ単独の分布を見ておく。最後のMEDVは持家価格(1000ドル単位)の中央値(Median Value)。

特徴量CHASはチャールズ川の川沿いに立地しているか否かのダミー変数で、0/1の2通りの値を持つ。いくつかの特徴量は値が集中していたり、離れたところのデータが多かったりしている。

import matplotlib.pyplot as plt
from sklearn.datasets import load_boston

boston_ds = load_boston()

X = boston_ds.data
y = boston_ds.target
feature_names = boston_ds.feature_names

n_features = X.shape[1]

fig, axs = plt.subplots(3, 5, figsize=(13, 7))
plt.subplots_adjust(hspace=0.4)
axs_1d = axs.reshape(1, -11)[0]

for ax, nf in zip(axs_1d, range(n_features)):
    ax.hist(X[:, nf], ec='k')
    ax.set_title(feature_names[nf])

axs_1d[n_features].hist(y, ec='k')
axs_1d[n_features].set_title("MEDV")

axs_1d[-1].axis('off')

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_boston

boston_ds = load_boston()

X = boston_ds.data

y = boston_ds.target

feature_names = boston_ds.feature_names

n_features = X.shape[1]

fig, axs = plt.subplots(3, 5, figsize=(13, 7))

plt.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -11)[0]

for ax, nf in zip(axs_1d, range(n_features)):

ax.hist(X[:, nf], ec='k')

ax.set_title(feature_names[nf])

axs_1d[n_features].hist(y, ec='k')

axs_1d[n_features].set_title("MEDV")

axs_1d[-1].axis('off')

plt.show()

各特徴量と価格の関係

13の特徴量1つ1つと価格の関係を散布図で見てみる。

比較的明らかな関係がみられるのはRM(1戸あたり部屋数)とLATAT(下位層の人口比率)で、この2つは特徴量自体の分布が比較的”整っている”。

NOX(NOx濃度)も特徴量の分布はそこそこなだらかだが、散布図では強い相関とは言い難い。

AGE(古い物件の比率)とDIS(職業紹介所への距離)はそれぞれ分布が単調減少／単調増加で、特徴量の大小と価格の高低の関係はある程度予想通りだがかなりばらついている。いずれの指標についてもMDEVがある値以下で密度が高くなっているように見えるのは興味深い。

import matplotlib.pyplot as plt
from sklearn.datasets import load_boston

boston_ds = load_boston()

X = boston_ds.data
target = boston_ds.target
feature_names = boston_ds.feature_names

n_features = X.shape[1]

fig, axs = plt.subplots(3, 5, figsize=(13, 7))
fig.subplots_adjust(hspace=0.4, wspace=0.4)

axs_1d = axs.reshape(1, -1)[0]

for ax, nf in zip(axs_1d, range(n_features)):
    ax.scatter(X[:, nf], target, s=5)
    ax.set_xlabel(feature_names[nf])
    ax.set_ylabel("MDEV")

for i in range(-2, 0): axs_1d[i].axis('off')

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_boston

boston_ds = load_boston()

X = boston_ds.data

target = boston_ds.target

feature_names = boston_ds.feature_names

n_features = X.shape[1]

fig, axs = plt.subplots(3, 5, figsize=(13, 7))

fig.subplots_adjust(hspace=0.4, wspace=0.4)

axs_1d = axs.reshape(1, -1)[0]

for ax, nf in zip(axs_1d, range(n_features)):

ax.scatter(X[:, nf], target, s=5)

ax.set_xlabel(feature_names[nf])

ax.set_ylabel("MDEV")

for i in range(-2, 0): axs_1d[i].axis('off')

plt.show()

2つの特徴量と価格の関係

個々の特徴量ごとの、価格との相関がある程度が明確だったRMとLSTATについて価格との関係を3次元で見てみる。

それぞれの相関がある程度明確なので、3次元でも一つの帯のようになっている。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_boston

boston_ds = load_boston()

X_df = pd.DataFrame(boston_ds.data, columns=boston_ds.feature_names)
x = np.array(X_df['RM'])
y = np.array(X_df['LSTAT'])
z = boston_ds.target

fig = plt.figure(figsize=(12, 4.8))

ax1 = fig.add_subplot(121, projection='3d')
ax1.scatter(x, y, z)
ax1.set_xlabel("RM")
ax1.set_ylabel("LSTAT")
ax1.set_zlabel("MDEV")

ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(x, y, z)
ax2.set_xlabel("RM")
ax2.set_ylabel("LSTAT")
ax2.set_zlabel("MDEV")

plt.show()

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

from sklearn.datasets import load_boston

boston_ds = load_boston()

X_df = pd.DataFrame(boston_ds.data, columns=boston_ds.feature_names)

x = np.array(X_df['RM'])

y = np.array(X_df['LSTAT'])

z = boston_ds.target

fig = plt.figure(figsize=(12, 4.8))

ax1 = fig.add_subplot(121, projection='3d')

ax1.scatter(x, y, z)

ax1.set_xlabel("RM")

ax1.set_ylabel("LSTAT")

ax1.set_zlabel("MDEV")

ax2 = fig.add_subplot(122, projection='3d')

ax2.scatter(x, y, z)

ax2.set_xlabel("RM")

ax2.set_ylabel("LSTAT")

ax2.set_zlabel("MDEV")

plt.show()

Boston house‐pricesデータセット

2020-03-25 / tau / コメントする

概要

Boston house-pricesデータセットは、カーネギーメロン大学のStatLibライブラリーから取得したもので、持家の価格とその持家が属する地域に関する指標からなる。

ボストンの各地域にある506の持家の価格の中央値に対して、その地域の犯罪発生率やNOx濃度など13の指標が得られる。

ここではPythonのscikit-learnにあるbostonデータの使い方をまとめる。

データの取得とデータ構造

Pythonで扱う場合、scikit-learnのdatasetsモジュールにあるload_breast_cancer()でデータを取得できる。データはBunchクラスのオブジェクト。

from sklearn.datasets import load_boston

boston_ds = load_boston()

for key, value in zip(boston_ds.keys(), boston_ds.values()):
    print("{}:\n{}\n".format(key, value))

from sklearn.datasets import load_boston

boston_ds = load_boston()

for key, value in zip(boston_ds.keys(), boston_ds.values()):

print("{}:\n{}\n".format(key, value))

データセットの構造は辞書型で、506の地域に関する13の特徴量と、当該地域における持家住宅の1000ドル単位の価格などのデータ。

data:
[[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
 ...
 [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
 [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
 [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

target:
[24.  21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15.  18.9 21.7 20.4
 18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8
 18.4 21.  12.7 14.5 13.2 13.1 13.5 18.9 20.  21.  24.7 30.8 34.9 26.6
 .....
 16.7 12.  14.6 21.4 23.  23.7 25.  21.8 20.6 21.2 19.1 20.6 15.2  7.
  8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9
 22.  11.9]

feature_names:
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

DESCR:
.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

.....

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.


filename:
C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\boston_house_prices.csv

data:

[[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]

[2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]

[2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]

...

[6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]

[1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]

[4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

target:

[24. 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15. 18.9 21.7 20.4

18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8

18.4 21. 12.7 14.5 13.2 13.1 13.5 18.9 20. 21. 24.7 30.8 34.9 26.6

.....

16.7 12. 14.6 21.4 23. 23.7 25. 21.8 20.6 21.2 19.1 20.6 15.2 7.

8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9

22. 11.9]

feature_names:

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'

'B' 'LSTAT']

DESCR:

.. _boston_dataset:

Boston house prices dataset

---------------------------

**Data Set Characteristics:**

:Number of Instances: 506

:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

.....

- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.

- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

filename:

C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\boston_house_prices.csv

データのキーは以下のようになっている。

from sklearn.datasets import load_boston

boston_ds = load_boston()

print(boston_ds.keys())

# dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])

from sklearn.datasets import load_boston

boston_ds = load_boston()

print(boston_ds.keys())

# dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])

データの内容

`'data'`～特徴量データセット

506の地域における13の指標を特徴量として格納した2次元配列。列のインデックスが特徴量の番号に対応している。

data:
[[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
 ...
 [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
 [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
 [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

data:

[[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]

[2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]

[2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]

...

[6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]

[1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]

[4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

`'target'`～住宅価格

506の地域における持家住宅の1000ドル単位の価格中央値

target:
[24.  21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15.  18.9 21.7 20.4
 18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8
 18.4 21.  12.7 14.5 13.2 13.1 13.5 18.9 20.  21.  24.7 30.8 34.9 26.6
 .....
 16.7 12.  14.6 21.4 23.  23.7 25.  21.8 20.6 21.2 19.1 20.6 15.2  7.
  8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9
 22.  11.9]

target:

[24. 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15. 18.9 21.7 20.4

18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8

18.4 21. 12.7 14.5 13.2 13.1 13.5 18.9 20. 21. 24.7 30.8 34.9 26.6

.....

16.7 12. 14.6 21.4 23. 23.7 25. 21.8 20.6 21.2 19.1 20.6 15.2 7.

8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9

22. 11.9]

`'feature_names'`～特徴名

13種類の特徴量の名称。

CRIM：町ごとの人口当たり犯罪率
ZN：25,000平方フィート以上の区画の住居用途地区比率
INDUS：町ごとの小売り以外の産業用途地区比率
CHAS：チャールズ川に関するダミー変数（1：川沿い、0：それ以外）
NOX：NOx濃度（10ppm単位）
RM：1戸あたり部屋数
AGE：1940年より前に建てられた持家物件の比率
DIS：ボストンの5つの職業紹介所への重みづけ平均距離
RAD：放射道路へのアクセス性
TAX：10,000ドルあたりの固定資産税総額
PTRATIO：生徒対教師の比率
B：1000(Bk – 0.63)^2（Bkは待ちにおける黒人比率）
LSTAT：下位層の人口比率(%)

feature_names:
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

feature_names:

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'

'B' 'LSTAT']

`'filename'`～ファイル名

CSVファイルのフルパス名が示されている。1行目にはデータ数、特徴量数が並んでおり、2行目に13の特徴量とターゲットの住宅価格、その後に506行のレコードに対する13列の特徴量と1列のターゲットデータが格納されている。このファイルにはDESCRに当たるデータは格納されていない。

'C:...\lib\site-packages\sklearn\datasets\data\boston_house_prices.csv'

1	'C:...\lib\site-packages\sklearn\datasets\data\boston_house_prices.csv'

`'DESCR'`～データセットの説明

データセットの説明。print(breast_ds_dataset['DESCR'])のようにprint文で整形表示される。

レコード数506個
属性は、13の数値／カテゴリー属性と、通常はターゲットに用いられる中央値

.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/


This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
.. topic:: References

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

.. _boston_dataset:

Boston house prices dataset

---------------------------

**Data Set Characteristics:**

:Number of Instances: 506

:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

:Attribute Information (in order):

- CRIM per capita crime rate by town

- ZN proportion of residential land zoned for lots over 25,000 sq.ft.

- INDUS proportion of non-retail business acres per town

- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)

- NOX nitric oxides concentration (parts per 10 million)

- RM average number of rooms per dwelling

- AGE proportion of owner-occupied units built prior to 1940

- DIS weighted distances to five Boston employment centres

- RAD index of accessibility to radial highways

- TAX full-value property-tax rate per $10,000

- PTRATIO pupil-teacher ratio by town

- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town

- LSTAT % lower status of the population

- MEDV Median value of owner-occupied homes in $1000's

:Missing Attribute Values: None

:Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.

https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic

prices and the demand for clean air', J. Environ. Economics & Management,

vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics

...', Wiley, 1980. N.B. Various transformations are used in the table on

pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression

problems.

.. topic:: References

- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.

データの利用

データの取得方法

bostonデータセットから各データを取り出すのに、以下の2つの方法がある。

辞書のキーを使って呼び出す（例：boston['DESCR']）
キーの文字列をプロパティーに指定する（例：boston.DESCR）

全レコードの特徴量データの取得

'data'から、506のレコードに関する13の特徴量が506行13列の2次元配列で得られる。13の特徴量は’feature_names’の13の特徴名に対応している。

from sklearn.datasets import load_boston

boston_ds = load_boston()

print(boston_ds.data)

# [[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
#  [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
#  [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
#  ...
#  [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
#  [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
#  [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

from sklearn.datasets import load_boston

boston_ds = load_boston()

print(boston_ds.data)

# [[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]

# [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]

# [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]

# ...

# [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]

# [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]

# [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]

特定の特徴量のデータのみ取得

特定の特徴量に関する全レコードのデータを取り出すときにはX[:, n]の形で指定する。

from sklearn.datasets import load_boston

boston_ds = load_boston()

features = boston_ds.feature_names
X = boston_ds.data
n_feature = 10

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))
print("feature data :\n{}".format(feature))

# feature name : PTRATIO
# feature data :
# [15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 15.2 15.2 15.2 21.
#  21.  21.  21.  21.  21.  21.  21.  21.  21.  21.  21.  21.  21.  21.
#  21.  21.  21.  21.  21.  21.  21.  19.2 19.2 19.2 19.2 18.3 18.3 17.9
#  ...
#  20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.1 20.1
#  20.1 20.1 20.1 19.2 19.2 19.2 19.2 19.2 19.2 19.2 19.2 21.  21.  21.
#  21.  21. ]

from sklearn.datasets import load_boston

boston_ds = load_boston()

features = boston_ds.feature_names

X = boston_ds.data

n_feature = 10

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))

print("feature data :\n{}".format(feature))

# feature name : PTRATIO

# feature data :

# [15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 15.2 15.2 15.2 21.

# 21. 21. 21. 21. 21. 21. 21. 21. 21. 21. 21. 21. 21. 21.

# 21. 21. 21. 21. 21. 21. 21. 19.2 19.2 19.2 19.2 18.3 18.3 17.9

# ...

# 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.1 20.1

# 20.1 20.1 20.1 19.2 19.2 19.2 19.2 19.2 19.2 19.2 19.2 21. 21. 21.

# 21. 21. ]

Pyplot – グラフの標準色

2020-03-22 / tau / コメントする

Pyplotのグラフを描くときに標準で使われる色を直接指定する方法。色名に"tab:blue"のように指定する。

import matplotlib.pyplot as plt

color_names = [
    "tab:blue",
    "tab:orange",
    "tab:green",
    "tab:red",
    "tab:purple",
    "tab:brown",
    "tab:pink",
    "tab:gray",
    "tab:olive",
    "tab:cyan",
]

rev_colors = [c for c in color_names[::-1]]

values = [1] * 10

fig, ax = plt.subplots()
fig.subplots_adjust(left=0.2)

ax.barh(rev_colors, values, color=rev_colors)
ax.tick_params(bottom=False, labelbottom=False)

plt.show()

import matplotlib.pyplot as plt

color_names = [

"tab:blue",

"tab:orange",

"tab:green",

"tab:red",

"tab:purple",

"tab:brown",

"tab:pink",

"tab:gray",

"tab:olive",

"tab:cyan",

]

rev_colors = [c for c in color_names[::-1]]

values = [1] * 10

fig, ax = plt.subplots()

fig.subplots_adjust(left=0.2)

ax.barh(rev_colors, values, color=rev_colors)

ax.tick_params(bottom=False, labelbottom=False)

plt.show()

waveデータセット – knn

2020-03-22 / tau / コメントする

概要

k-最近傍回帰の例として、scikit-learnのwaveデータにKNeighborsRegressorを適用してみた結果。

近傍点数とクラス分類の挙動

訓練データとして10個のwaveデータを訓練データとして与え、2つのテストデータの予測するのに、近傍点数を1, 2, 3と変えた場合の様子を見てみる。

近傍点数=1の場合

2つのテストデータの特徴量の値に最も近い特徴量を持つ訓練データが選ばれ、その属性値がそのままテストデータの属性値となっている。

近傍点数=2の場合

テストデータの特徴量に最も近い方から1番目、2番目の特徴量を持つ訓練データが選ばれ、それらの属性値の平均がテストデータの属性値となっている。

近傍点数=3の場合

同様に、テストデータの特徴量に最も近い3つの訓練データの属性の平均がテストデータの属性値となっている。

実行コード

上記の計算のコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from mglearn.datasets import make_wave

X_train, y_train = make_wave(n_samples=10)

reg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train, y_train)

X_test = np.array([[-1], [1]])
y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)
print(neigh_ind)

fig, ax = plt.subplots(figsize=(8.0, 4.8))

xmin, xmax = -3, 3
ymin, ymax = -3, 3

ax.scatter(X_train, y_train, marker='o', s=20)
ax.scatter(X_test, y_pred, marker='*', s=120)

for test, pred, ind in zip(X_test, y_pred, neigh_ind):
    for neigh in ind:
        ax.plot([test, test], [ymin, ymax], c='gray', linestyle='dashed')
        ax.plot(
            [test[0], X_train[neigh, 0]], [pred, y_train[neigh]],
            color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):
    ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.1, y + 0.08))
for x, y in zip(X_test, y_pred):
    ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.2, y - 0.3))

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)

ax.set_xlabel("feature")
ax.set_ylabel("prediction")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.neighbors import KNeighborsRegressor

from mglearn.datasets import make_wave

X_train, y_train = make_wave(n_samples=10)

reg = KNeighborsRegressor(n_neighbors=3)

reg.fit(X_train, y_train)

X_test = np.array([[-1], [1]])

y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

print(neigh_ind)

fig, ax = plt.subplots(figsize=(8.0, 4.8))

xmin, xmax = -3, 3

ymin, ymax = -3, 3

ax.scatter(X_train, y_train, marker='o', s=20)

ax.scatter(X_test, y_pred, marker='*', s=120)

for test, pred, ind in zip(X_test, y_pred, neigh_ind):

for neigh in ind:

ax.plot([test, test], [ymin, ymax], c='gray', linestyle='dashed')

ax.plot(

[test[0], X_train[neigh, 0]], [pred, y_train[neigh]],

color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):

ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.1, y + 0.08))

for x, y in zip(X_test, y_pred):

ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.2, y - 0.3))

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_xlabel("feature")

ax.set_ylabel("prediction")

plt.show()

knnの精度

O’Reillyの”Pythonではじめる機械学習”中、KNeighborsRegressorのwaveデータに対する精度が計算されている。40サンプルのwaveデータを発生させ訓練データとテストデータに分け、テストデータに対するR²スコアが0.83となることが示されている。実際に計算してみると、確かに同じ値となる。

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=40)

X_train, X_test, y_train, y_test =\
    train_test_split(X_source, y_source, random_state=0)

reg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)

print("R^2 score:{:6.3f}".format(reg.score(X_test, y_test)))

# R^2 score: 0.834

import numpy as np

from sklearn.neighbors import KNeighborsRegressor

from sklearn.model_selection import train_test_split

from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=40)

X_train, X_test, y_train, y_test =\

train_test_split(X_source, y_source, random_state=0)

reg = KNeighborsRegressor(n_neighbors=3)

reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

print("R^2 score:{:6.3f}".format(reg.score(X_test, y_test)))

# R^2 score: 0.834

これを見ると比較的高い精度のように見えるが、train_test_split()の引数random_stateを変化させてみると以下のように精度はばらつく。乱数系列が異なると精度が0.3未満の場合もあるが、全体としてみると0.6～0.7あたりとなりそうである。

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=40)

reg = KNeighborsRegressor(n_neighbors=3)

print("random_state -> R^2")

for random_state in range(0, 10):
    X_train, X_test, y_train, y_test =\
        train_test_split(X_source, y_source, random_state=random_state)
    reg.fit(X_train, y_train)
    y_pred = reg.predict(X_test)

    print("{} -> {:6.3f}".format(random_state, reg.score(X_test, y_test)))

# random_state -> R^2
# 0 ->  0.834
# 1 ->  0.581
# 2 ->  0.798
# 3 ->  0.281
# 4 ->  0.773
# 5 ->  0.738
# 6 ->  0.554
# 7 ->  0.494
# 8 ->  0.678
# 9 ->  0.801

import numpy as np

from sklearn.neighbors import KNeighborsRegressor

from sklearn.model_selection import train_test_split

from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=40)

reg = KNeighborsRegressor(n_neighbors=3)

print("random_state -> R^2")

for random_state in range(0, 10):

X_train, X_test, y_train, y_test =\

train_test_split(X_source, y_source, random_state=random_state)

reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

print("{} -> {:6.3f}".format(random_state, reg.score(X_test, y_test)))

# random_state -> R^2

# 0 -> 0.834

# 1 -> 0.581

# 2 -> 0.798

# 3 -> 0.281

# 4 -> 0.773

# 5 -> 0.738

# 6 -> 0.554

# 7 -> 0.494

# 8 -> 0.678

# 9 -> 0.801

ためしにmake_wave(n_samples=1000)としてみると、結果は以下の通りとなり、精度は0.67程度（平均は0.677）と一定してくる。

random_state -> R^2
0 ->  0.679
1 ->  0.662
2 ->  0.682
3 ->  0.672
4 ->  0.680
5 ->  0.697
6 ->  0.712
7 ->  0.682
8 ->  0.661
9 ->  0.641

random_state -> R^2

0 -> 0.679

1 -> 0.662

2 -> 0.682

3 -> 0.672

4 -> 0.680

5 -> 0.697

6 -> 0.712

7 -> 0.682

8 -> 0.661

9 -> 0.641

予測カーブ

訓練データが少ない場合

40個のwaveデータに対して、n_neighborsを変化させたときの予測カーブを見てみる。

n_neighbors=1の時は、全ての訓練データを通るような線となる
n_neighborsが多くなるほど滑らかになる
n_neighborsがかなり大きくなると水平に近くなる
n_neighborsが訓練データ数と同じになると、予測線は水平になる（任意の特徴量に対して、全ての点の平均を計算しているため）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from mglearn.datasets import make_wave

X_train, y_train = make_wave(n_samples=40)
xmin = np.min(X_train[:, 0])
xmax = np.max(X_train[:, 0])
X_test = np.linspace(xmin, xmax, 200).reshape(-1, 1)

fig, axs = plt.subplots(2, 3, figsize=(11, 6.4))
plt.subplots_adjust(hspace=0.4, wspace=0.4)

n_neighbors_list=[1, 2, 8, 16, 32, 40]
axs_1d = axs.reshape(1, -1)[0]

for ax, n_neighbors in zip(axs_1d, n_neighbors_list):
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    y_pred = reg.predict(X_test)

    ax.scatter(X_train[:, 0], y_train, zorder=2, s=20, color='tab:blue')
    ax.plot(X_test, y_pred, zorder=1, color='tab:orange')

    ax.set_title("n_neighbors={}".format(n_neighbors))
    ax.set_xlabel("feature")
    ax.set_ylabel("target")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.neighbors import KNeighborsRegressor

from mglearn.datasets import make_wave

X_train, y_train = make_wave(n_samples=40)

xmin = np.min(X_train[:, 0])

xmax = np.max(X_train[:, 0])

X_test = np.linspace(xmin, xmax, 200).reshape(-1, 1)

fig, axs = plt.subplots(2, 3, figsize=(11, 6.4))

plt.subplots_adjust(hspace=0.4, wspace=0.4)

n_neighbors_list=[1, 2, 8, 16, 32, 40]

axs_1d = axs.reshape(1, -1)[0]

for ax, n_neighbors in zip(axs_1d, n_neighbors_list):

reg = KNeighborsRegressor(n_neighbors=n_neighbors)

reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

ax.scatter(X_train[:, 0], y_train, zorder=2, s=20, color='tab:blue')

ax.plot(X_test, y_pred, zorder=1, color='tab:orange')

ax.set_title("n_neighbors={}".format(n_neighbors))

ax.set_xlabel("feature")

ax.set_ylabel("target")

plt.show()

訓練データが多い場合

今度はwaveデータでn_samples=200と数を多くしてみる。データ数を多くするとその名の通り、上下に波打ちながら増加している様子が見られる。これに対してn_neighborsを変化させたのが以下の図。

n_neighbors=10～20あたりで滑らかに、かつ波打つ状況が曲線で再現されている。

n_samples=300として訓練データに200を振り分け、n_neighborsを変化させたときのスコアは以下の通り。n_neighbors=20あたりで精度が最もよさそうである。

あるデータが得られたとき、その科学的なメカニズムは置いておいて、とりあえずデータから予測値を再現したいときにはそれなりに使えるかもしれない。

n_neighbors -> R^2
5 ->  0.754
10 ->  0.788
15 ->  0.789
20 ->  0.792
25 ->  0.777
50 ->  0.737
100 ->  0.613
200 -> -0.022

n_neighbors -> R^2

5 -> 0.754

10 -> 0.788

15 -> 0.789

20 -> 0.792

25 -> 0.777

50 -> 0.737

100 -> 0.613

200 -> -0.022

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=300)

X_train, X_test, y_train, y_test =\
    train_test_split(X_source, y_source, train_size=200, random_state=0)

n_neighbors_list = [5, 10, 15, 20, 25, 50, 100, 200]

print("n_neighbors -> R^2")

for n_neighbors in n_neighbors_list:
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    y_pred = reg.predict(X_test)

    print("{} -> {:6.3f}".format(n_neighbors, reg.score(X_test, y_test)))

import numpy as np

from sklearn.neighbors import KNeighborsRegressor

from sklearn.model_selection import train_test_split

from mglearn.datasets import make_wave

X_source, y_source = make_wave(n_samples=300)

X_train, X_test, y_train, y_test =\

train_test_split(X_source, y_source, train_size=200, random_state=0)

n_neighbors_list = [5, 10, 15, 20, 25, 50, 100, 200]

print("n_neighbors -> R^2")

for n_neighbors in n_neighbors_list:

reg = KNeighborsRegressor(n_neighbors=n_neighbors)

reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

print("{} -> {:6.3f}".format(n_neighbors, reg.score(X_test, y_test)))

pyplot – zorder～グラフの描画順

2020-03-22 / tau / コメントする

pyplotでグラフを描画する際、点よりも線の方が上になって見栄えが悪い・・・といった場合に、どのグラフから上にするかという指定が必要になる。

グラフ描画の優先性はplot()やscatter()などのグラフメソッドの引数にzorderを指定して実現できる。zorderに指定した値がより大きいグラフの方が上のレイヤーになる。指定できる値は正負の実数。

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 2, figsize=(9.6, 3.6))

x = np.linspace(-np.pi, np.pi, 40)
y = np.sin(x)

ax[0].plot(x, y, color='tab:orange')
ax[0].scatter(x, y, color='tab:blue')

ax[1].plot(x, y, zorder=-0.1, color='tab:orange')
ax[1].scatter(x, y, zorder=1, color='tab:blue')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 2, figsize=(9.6, 3.6))

x = np.linspace(-np.pi, np.pi, 40)

y = np.sin(x)

ax[0].plot(x, y, color='tab:orange')

ax[0].scatter(x, y, color='tab:blue')

ax[1].plot(x, y, zorder=-0.1, color='tab:orange')

ax[1].scatter(x, y, zorder=1, color='tab:blue')

plt.show()

左のグラフは後から実行しているscatterがplotの下に表示されている。

右のグラフではzorderを指定しており、scatterの方が値が大きいため上のレイヤーに表示されている。

forgeデータセット – knn

2020-03-22 / tau / コメントする

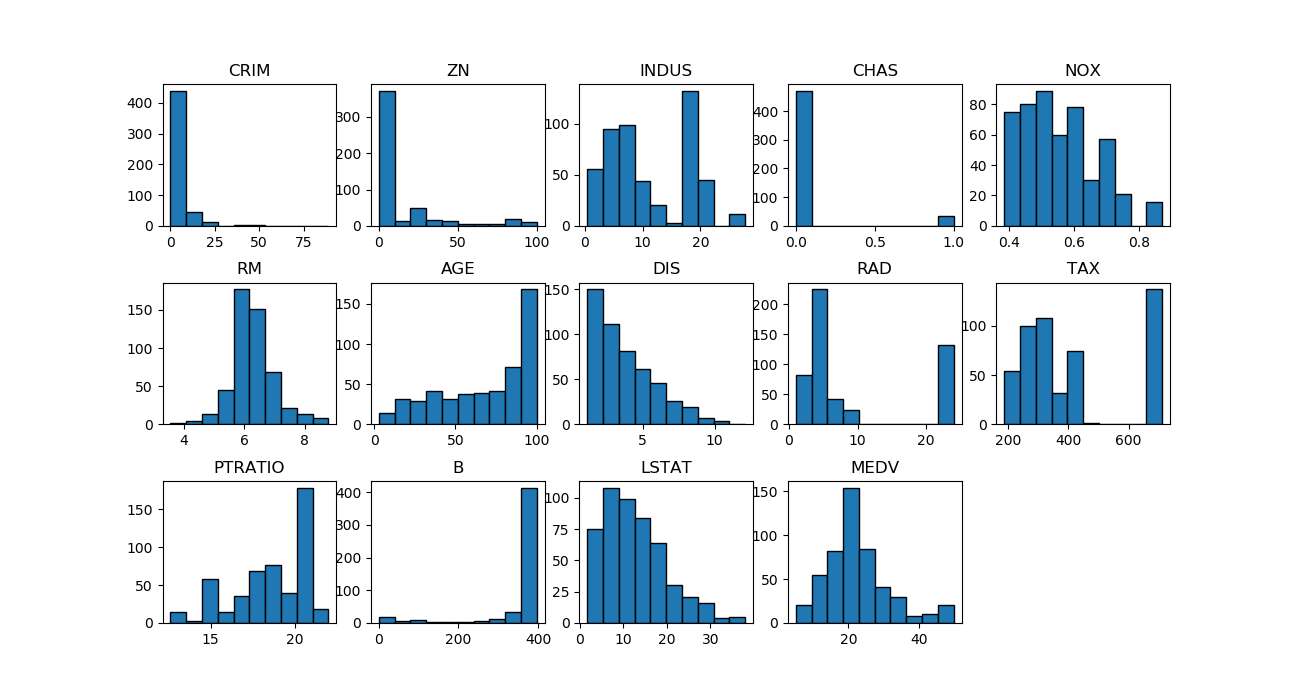
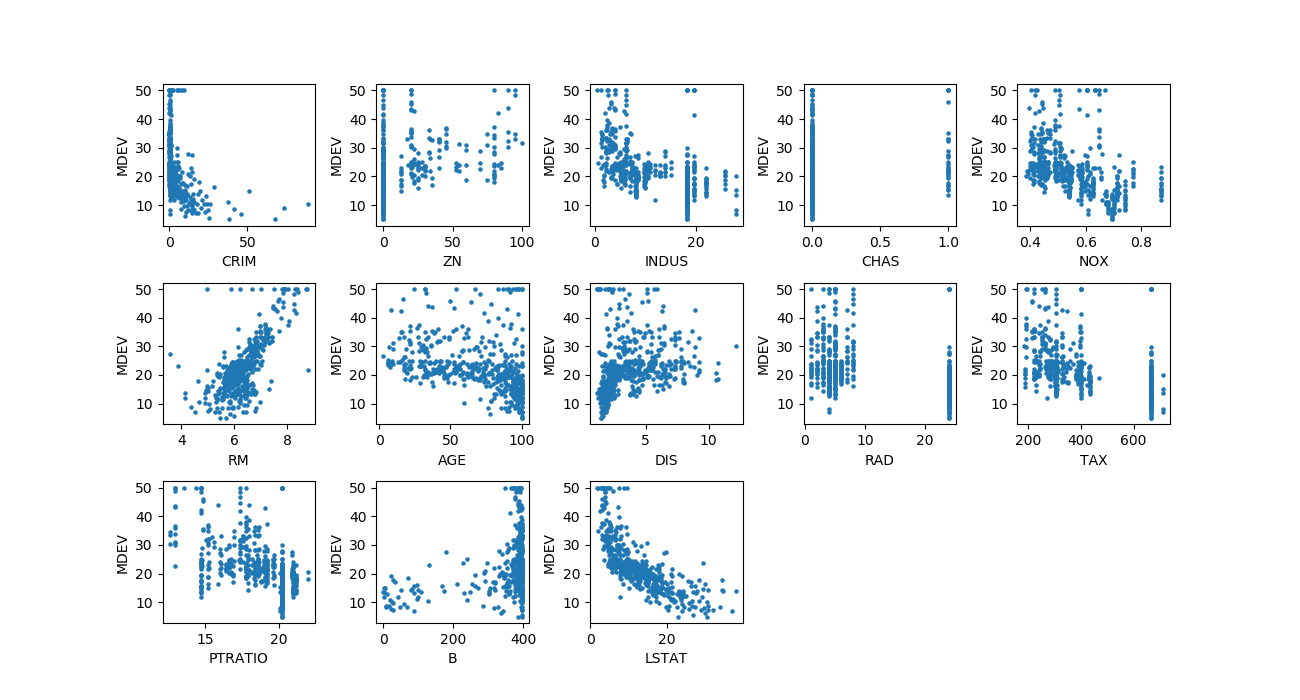
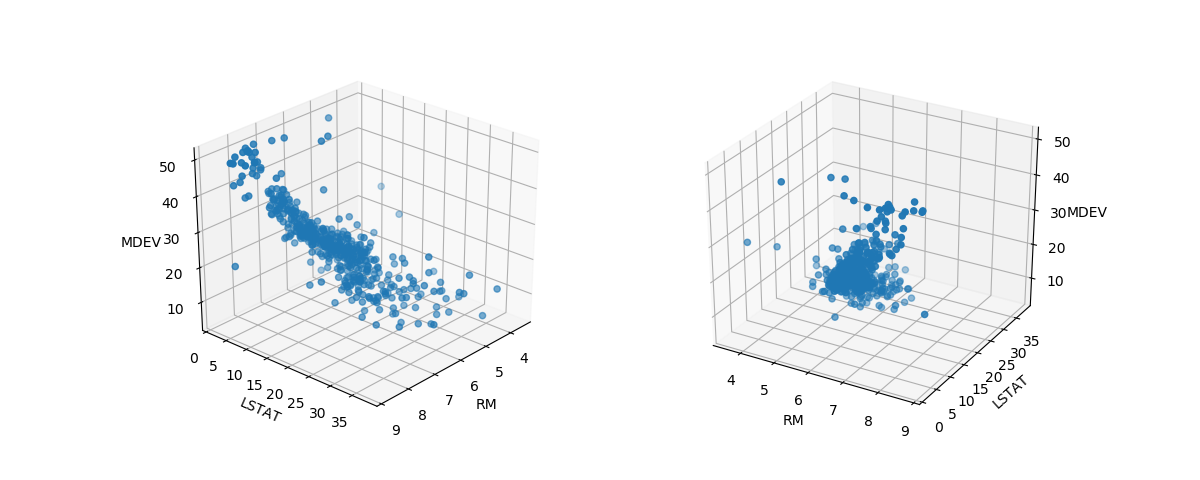
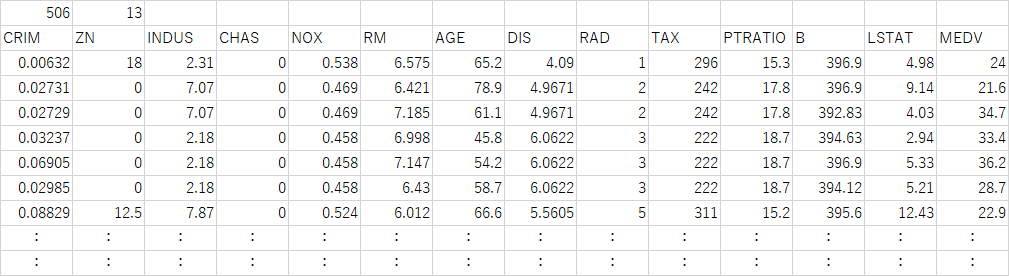
概要

ここでは、Pythonのscikit-learnパッケージのKNeighborsClassifierクラスにmglearnパッケージのforgeデータを適用してknnの挙動を確認する。

近傍点数を変化させたときのクラス分類の挙動や学習率曲線についてみていく。

近傍点数によるクラス分類の挙動

近傍点数=1の場合

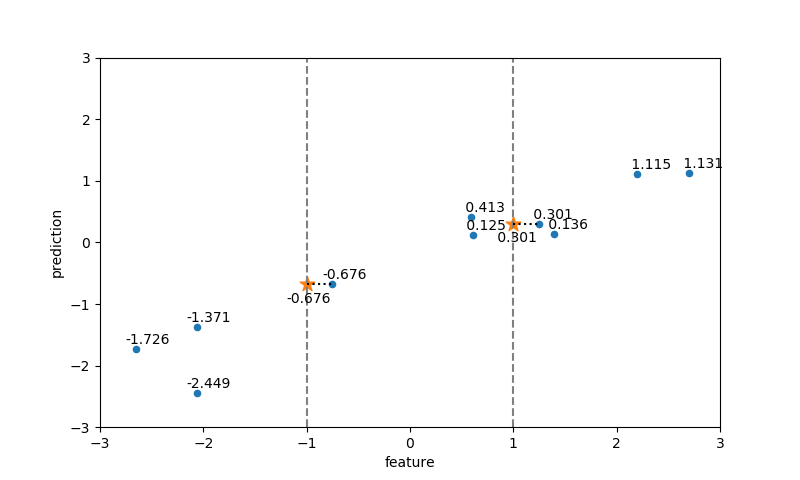
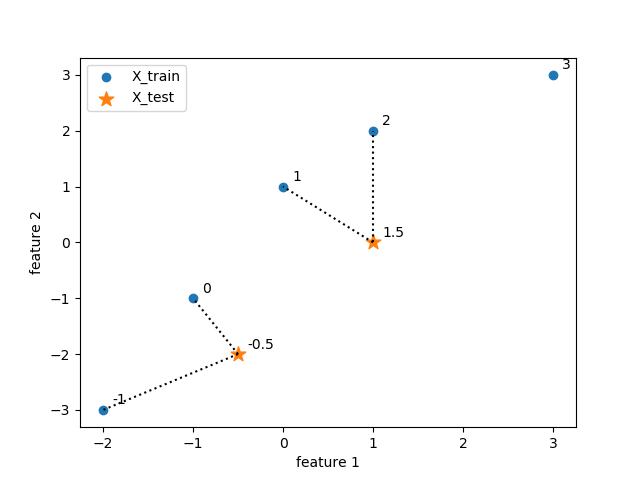
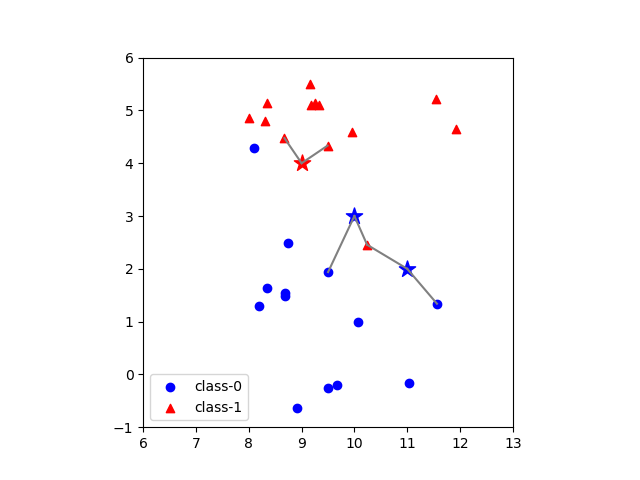
データセットとしてmglearnで提供されているforgeデータを用いて、近傍点数=1とした場合の、3つのテストデータのクラス判定を以下に示す。各テストデータに対して最も距離(この場合はユークリッド距離)が近い点1つが定まり、その点のクラステストデータのクラスとして決定している。

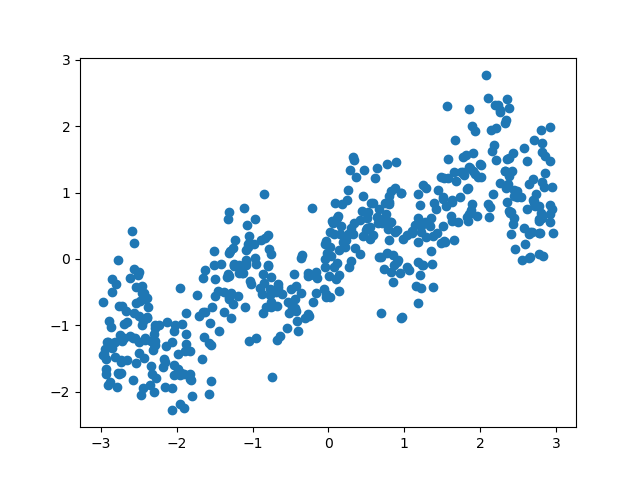
なお、いろいろなところで見かけるforgeデータセットの散布図は当該データセットの特徴量0(横軸)と特徴量1(縦軸)の最小値と最大値に合わせて表示しており、軸目盛の比率が等しくない。ここでは、距離計算に視覚上の齟齬が生じないように、縦軸と横軸の比率を同じとしている。

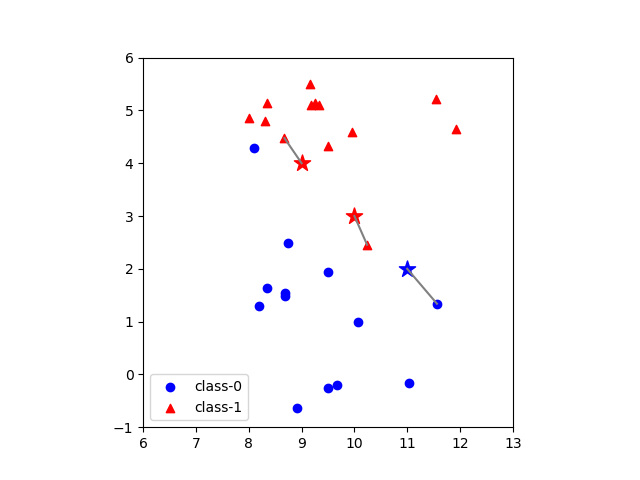
後の計算のために、このグラフ描画のコードを以下に示す。

import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from mglearn.datasets import make_forge

X, y = make_forge()

clfr = KNeighborsClassifier(n_neighbors=1)
clfr.fit(X, y)

col = ['blue', 'red']

test_points = [[9., 4.], [10., 3.], [11., 2.]]
nb_dist, nb_idx = clfr.kneighbors(test_points)
test_pred = clfr.predict(test_points)

fig, ax = plt.subplots()

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o', c=col[0], label="class-0")
ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^', c=col[1], label="class-1")

ax.legend(loc="lower left")

for pts, cls, ids, dists in zip(test_points, test_pred, nb_idx, nb_dist):
    print(pts)
    ax.scatter(pts[0], pts[1], marker='*', s=150, c=col[cls])
    for id, dst in zip(ids, dists):
        ax.plot([pts[0], X[id, 0]], [pts[1], X[id, 1]], c='gray')
        print(" [{:7.4f}, {:7.4f}] - {:7.4f}".format(X[id, 0], X[id, 1], dst))

plt.show()

import matplotlib.pyplot as plt

from sklearn.neighbors import KNeighborsClassifier

from mglearn.datasets import make_forge

X, y = make_forge()

clfr = KNeighborsClassifier(n_neighbors=1)

clfr.fit(X, y)

col = ['blue', 'red']

test_points = [[9., 4.], [10., 3.], [11., 2.]]

nb_dist, nb_idx = clfr.kneighbors(test_points)

test_pred = clfr.predict(test_points)

fig, ax = plt.subplots()

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o', c=col[0], label="class-0")

ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^', c=col[1], label="class-1")

ax.legend(loc="lower left")

for pts, cls, ids, dists in zip(test_points, test_pred, nb_idx, nb_dist):

print(pts)

ax.scatter(pts[0], pts[1], marker='*', s=150, c=col[cls])

for id, dst in zip(ids, dists):

ax.plot([pts[0], X[id, 0]], [pts[1], X[id, 1]], c='gray')

print(" [{:7.4f}, {:7.4f}] - {:7.4f}".format(X[id, 0], X[id, 1], dst))

plt.show()

概要は以下の通り。

5行目でforgeデータセットを準備
7行目で近傍点数を1で指定してクラス分類器を構築
8行目で訓練データとしてforgeデータを与える
12行目で3つのテストデータを準備
13行目でテストデータに対する近傍点のインデックスとテストデータまでの距離を獲得
14行目でテストデータのクラスを決定
18-19行目で訓練データの散布図を描画
23行目で、テストデータとそのクラス決定結果、クラス決定に用いられた点群のインデックス、テストデータと各点の距離を並行してループ
- 24行目でテストデータの座標を出力
- 25行目でテストデータを描画
- 26行目のループで、テストデータごとの近傍点に関する処理を実行
  - 27行目でテストデータと近傍点の間に直線を描画
  - 28行目で近傍点とテストデータからの距離を出力

出力結果は以下の通りで、各予測点に対して近傍点が1つ決定されている。

[9.0, 4.0]
 [ 8.6749,  4.4757] -  0.5762
[10.0, 3.0]
 [10.2403,  2.4554] -  0.5952
[11.0, 2.0]
 [11.5640,  1.3389] -  0.8689

[9.0, 4.0]

[ 8.6749, 4.4757] - 0.5762

[10.0, 3.0]

[10.2403, 2.4554] - 0.5952

[11.0, 2.0]

[11.5640, 1.3389] - 0.8689

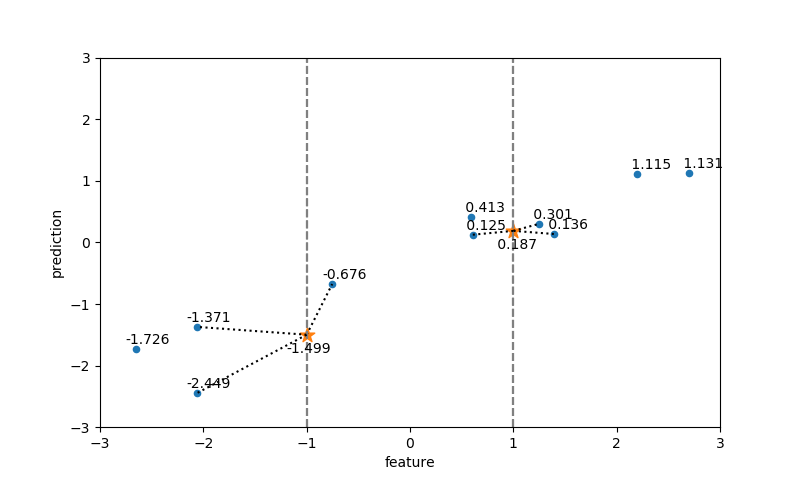
近傍点数=3の場合

先の例で、コードの7行目で近傍点=3で指定してクラス分類器を構築する。

clfr = KNeighborsClassifier(n_neighbors=3)

1	clfr = KNeighborsClassifier(n_neighbors=3)

一般にknnでは、テストデータに対して複数の近傍点を指定する場合、各近傍点のクラスのうち最も多いものをテストデータのクラスとする(多数決)。

[9.0, 4.0]
 [ 8.6749,  4.4757] -  0.5762
 [ 9.4912,  4.3322] -  0.5930
 [ 8.1062,  4.2870] -  0.9387
[10.0, 3.0]
 [10.2403,  2.4554] -  0.5952
 [ 9.5017,  1.9382] -  1.1729
 [ 8.7337,  2.4916] -  1.3645
[11.0, 2.0]
 [11.5640,  1.3389] -  0.8689
 [10.2403,  2.4554] -  0.8858
 [10.0639,  0.9908] -  1.3765

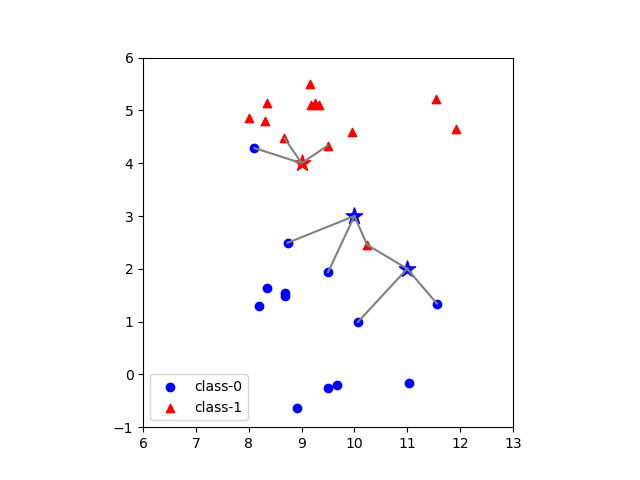
[9.0, 4.0]

[ 8.6749, 4.4757] - 0.5762

[ 9.4912, 4.3322] - 0.5930

[ 8.1062, 4.2870] - 0.9387

[10.0, 3.0]

[10.2403, 2.4554] - 0.5952

[ 9.5017, 1.9382] - 1.1729

[ 8.7337, 2.4916] - 1.3645

[11.0, 2.0]

[11.5640, 1.3389] - 0.8689

[10.2403, 2.4554] - 0.8858

[10.0639, 0.9908] - 1.3765

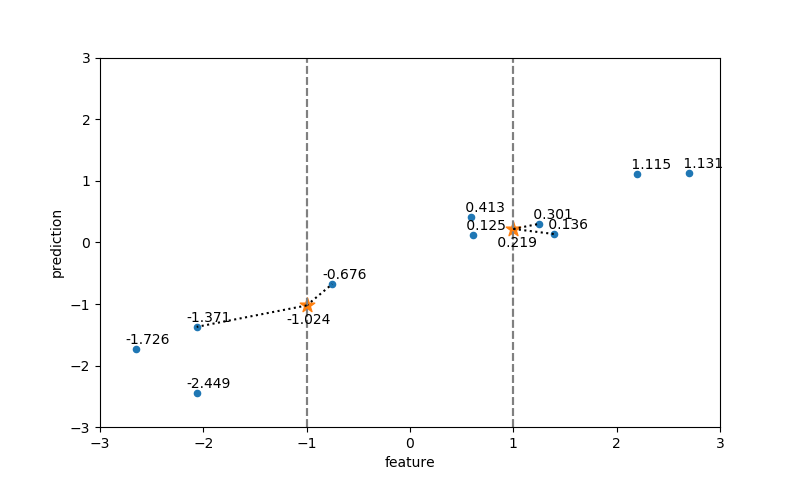
近傍点数=2の場合

テストデータのクラスを近傍点のクラスの多数決で求めるとすると、近傍点数が偶数の時の処理が問題になる。KNeighborsClassifierの場合、偶数でクラス分類が拮抗する場合は、クラス番号が最も小さいものに割り当てられるらしい。実際、n_neighbors=2としたときの3つのテストデータのうち中央の点(10.0, 3.0)については、赤い点(10.24, 2.45)～class-1～距離0.5952の方が青い点(9.5017, 1.9382)～class-0～距離1.1729よりも距離は近いがクラス番号が0である青い点のクラスで判定されている。

[9.0, 4.0]
 [ 8.6749,  4.4757] -  0.5762
 [ 9.4912,  4.3322] -  0.5930
[10.0, 3.0]
 [10.2403,  2.4554] -  0.5952
 [ 9.5017,  1.9382] -  1.1729
[11.0, 2.0]
 [11.5640,  1.3389] -  0.8689
 [10.2403,  2.4554] -  0.8858

[9.0, 4.0]

[ 8.6749, 4.4757] - 0.5762

[ 9.4912, 4.3322] - 0.5930

[10.0, 3.0]

[10.2403, 2.4554] - 0.5952

[ 9.5017, 1.9382] - 1.1729

[11.0, 2.0]

[11.5640, 1.3389] - 0.8689

[10.2403, 2.4554] - 0.8858

偶数の点で多数決で拮抗した場合には、最も近い点のクラスで決定する、平均距離が近い方のクラスで決定するといった方法が考えられるが、この場合は必ず番号が小さなクラスが選ばれるため、若干結果に偏りがでやすいのでは、と考える。

決定境界

近傍点の数を変えた時の決定境界の変化を確認する。k近傍法はscikit-learnのKNeighborsClassifierクラスを利用する。

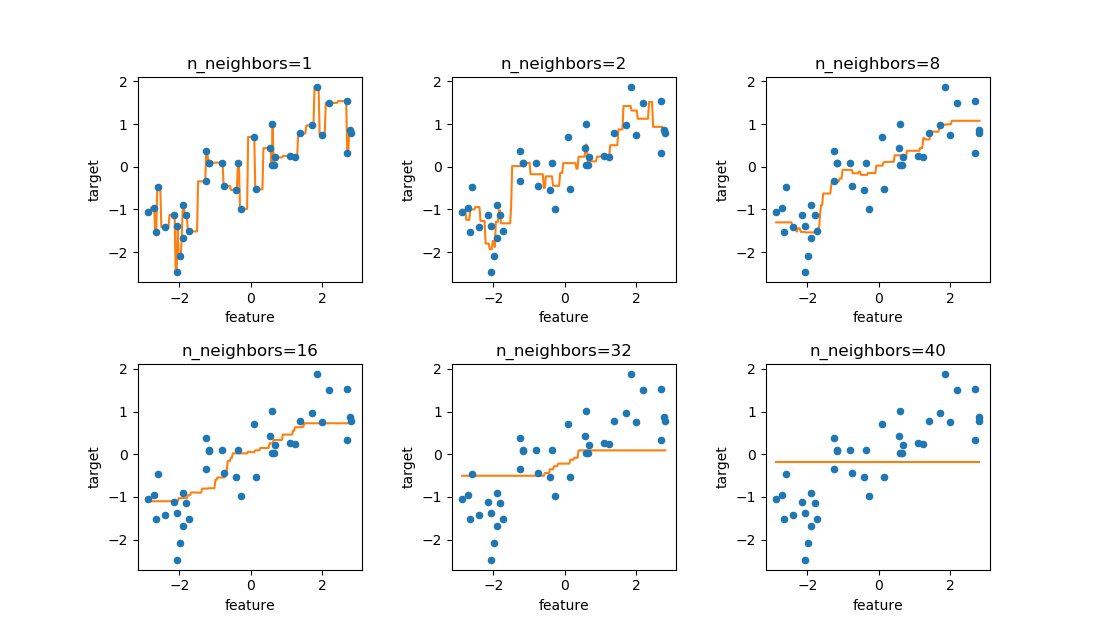
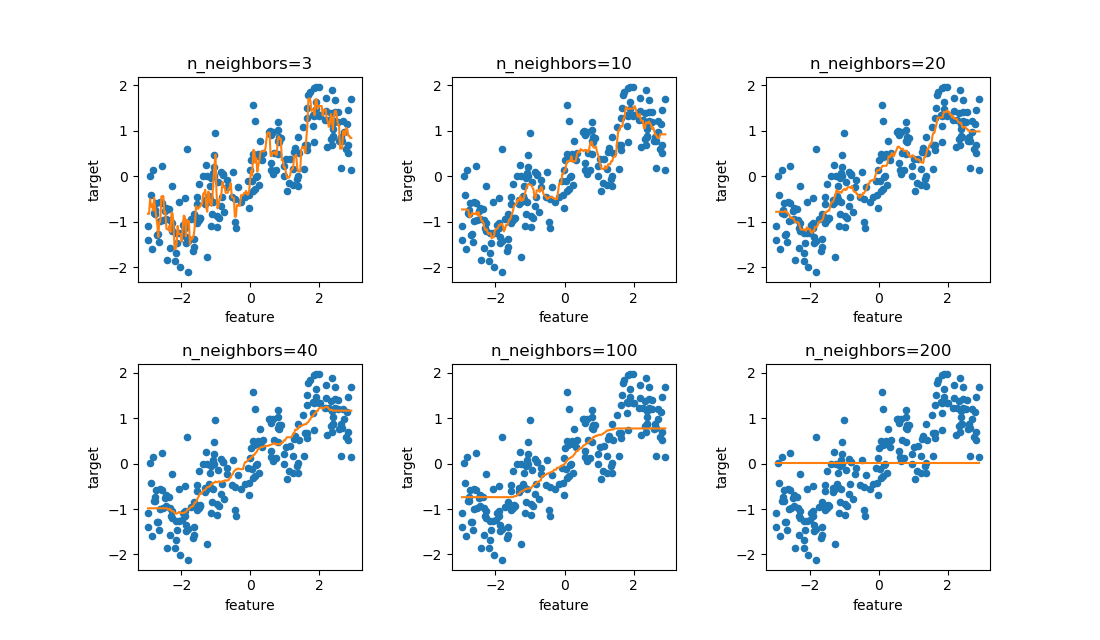
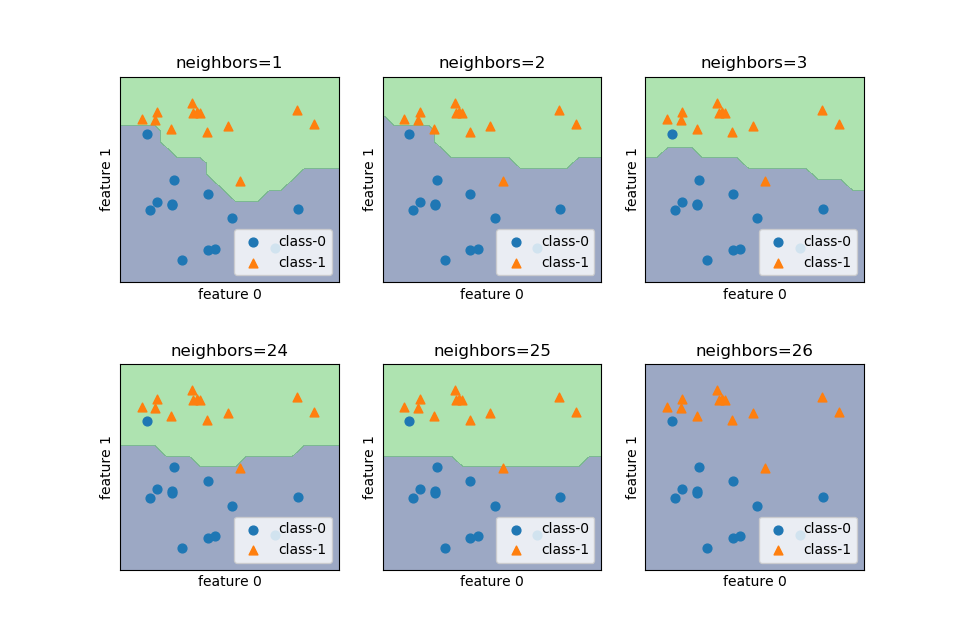
近傍点の数を1, 2, 3, …と変化させたときの決定境界の変化は以下の通り。

近傍点数が少ないときは訓練データにフィットするよう決定境界が複雑になるが、近傍点数が多いと決定境界は滑らかになる。特に近傍点数が訓練データの点数に等しいとき、全訓練データの多数決でクラス決定され、全領域で判定結果が同じとなる(この場合は近傍点数26が偶数なので、クラス番号の小さいclass-0で決定されている)。

この図を描画したコードを以下に示す。

7行目、引数で与えたAxesに対して決定境界を描く関数を定義
- 18行目、決定境界をcontourf()を利用して描いている
21行目、引数で与えたAxesに対してクラスごとに色分けした散布図を描く関数を定義
54行目、2次元配列のAxesを1次元配列として扱っている

import numpy as np
import matplotlib.pyplot as plt
from mglearn.datasets import make_forge
from sklearn.neighbors import KNeighborsClassifier


def draw_decision_boundary(ax, n_neighbors, X, y, X0_field, X1_field):
    clsfr = KNeighborsClassifier(n_neighbors=n_neighbors)

    clsfr.fit(X, y)

    y_predicted = np.empty((len(X1_field), len(X0_field)))

    for row, x1 in enumerate(X1_field):
        for col, x0 in enumerate(X0_field):
            y_predicted[row, col] = clsfr.predict(np.array([[x0, x1]]))

    ax.contourf(X0_field, X1_field, y_predicted, levels=1, alpha=0.5)


def draw_scatter(ax, X0, X1, xlim, ylim):
    ax.scatter(X0[y==0], X1[y==0], marker='o', s=40, label="class-0")
    ax.scatter(X0[y==1], X1[y==1], marker='^', s=40, label="class-1")

    ax.set_xlim(xlim[0], xlim[1])
    ax.set_ylim(ylim[0], ylim[1])

    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")

    ax.tick_params(labelbottom=False, labelleft=False)
    ax.tick_params(bottom=False, left=False)

    ax.legend(loc='lower right')


X, y = make_forge()

X0_scatter = X[:, 0]
X1_scatter = X[:, 1]

n_X0_field, n_X1_field = 20, 20
y_predicted = np.empty((n_X1_field, n_X0_field))

xlim = (7.5, 12.5)
ylim = (-1.5, 6.5)
X0_field = np.linspace(xlim[0], xlim[1], n_X0_field)
X1_field = np.linspace(ylim[0], ylim[1], n_X1_field)

fig, axs = plt.subplots(2, 3, figsize=(9.6, 6.4))
fig.subplots_adjust(hspace= 0.4)

n_neighbors_list = [1, 2, 3, 24, 25, 26]
axs_1d = axs.reshape(1, -1)[0]

for n_neighbors, ax in zip(n_neighbors_list, axs_1d):
    ax.set_title("neighbors={}".format(n_neighbors))
    draw_decision_boundary(ax, n_neighbors, X, y, X0_field, X1_field)
    draw_scatter(ax, X0_scatter, X1_scatter, xlim, ylim)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mglearn.datasets import make_forge

from sklearn.neighbors import KNeighborsClassifier

def draw_decision_boundary(ax, n_neighbors, X, y, X0_field, X1_field):

clsfr = KNeighborsClassifier(n_neighbors=n_neighbors)

clsfr.fit(X, y)

y_predicted = np.empty((len(X1_field), len(X0_field)))

for row, x1 in enumerate(X1_field):

for col, x0 in enumerate(X0_field):

y_predicted[row, col] = clsfr.predict(np.array([[x0, x1]]))

ax.contourf(X0_field, X1_field, y_predicted, levels=1, alpha=0.5)

def draw_scatter(ax, X0, X1, xlim, ylim):

ax.scatter(X0[y==0], X1[y==0], marker='o', s=40, label="class-0")

ax.scatter(X0[y==1], X1[y==1], marker='^', s=40, label="class-1")

ax.set_xlim(xlim[0], xlim[1])

ax.set_ylim(ylim[0], ylim[1])

ax.set_xlabel("feature 0")

ax.set_ylabel("feature 1")

ax.tick_params(labelbottom=False, labelleft=False)

ax.tick_params(bottom=False, left=False)

ax.legend(loc='lower right')

X, y = make_forge()

X0_scatter = X[:, 0]

X1_scatter = X[:, 1]

n_X0_field, n_X1_field = 20, 20

y_predicted = np.empty((n_X1_field, n_X0_field))

xlim = (7.5, 12.5)

ylim = (-1.5, 6.5)

X0_field = np.linspace(xlim[0], xlim[1], n_X0_field)

X1_field = np.linspace(ylim[0], ylim[1], n_X1_field)

fig, axs = plt.subplots(2, 3, figsize=(9.6, 6.4))

fig.subplots_adjust(hspace= 0.4)

n_neighbors_list = [1, 2, 3, 24, 25, 26]

axs_1d = axs.reshape(1, -1)[0]

for n_neighbors, ax in zip(n_neighbors_list, axs_1d):

ax.set_title("neighbors={}".format(n_neighbors))

draw_decision_boundary(ax, n_neighbors, X, y, X0_field, X1_field)

draw_scatter(ax, X0_scatter, X1_scatter, xlim, ylim)

plt.show()

k-最近傍法 – 回帰

2020-03-22 / tau / コメントする

概要

k-最近傍法(k nearest neighbors: knn)による回帰は、テストデータの近傍の訓練データからテストデータの属性値を決定する。その手法は単純で、特段の学習処理はせず、訓練データセットの特徴量と属性値を記憶するのみで、テストデータが与えられたときに近傍点から属性値を決定する。手順は以下の通り。

パッケージをインポートする
特徴量と属性値のデータセットを記憶する
テストデータが与えられたら、特徴量空間の中で近傍点を選ぶ
近傍点の属性値からテストデータの属性値を決定する

パラメーターは近傍点の数で、1以上訓練データの数まで任意に増やすことができる。

利用方法

手順

scikit-learnのKNeighborsRegressorクラスの利用方法は以下の通り。

sklearn.neighborsからKNeighborsRegressorをインポート
コンストラクターの引数に近傍点数n_neighborsを指定して、KNeighborsRegressorのインスタンスを生成
fit()メソッドに訓練データの特徴量と属性値を与えて学習
predict()メソッドにテストデータの特徴量を指定して、属性値を予測
必要に応じて、kneighbors()メソッドでテストデータの近傍点情報を取得

パッケージのインポート

k-最近傍回帰のパッケージは以下でインポートする。

from sklearn.neighbors import KNeighborsRegressor

1	from sklearn.neighbors import KNeighborsRegressor

コンストラクター

KNeighborsClassifier(n_neighbors=n): nは近傍点の数でデフォルトは5。この他の引数に、近傍点を発見するアルゴリズムなどが指定できるようだ。

訓練

fit()メソッドに与える訓練データは、特徴量セットと属性値の2つ。

fit(X, y): Xは訓練データセットの特徴量データで、データ数×特徴量数の2次元配列。yは訓練データセットの属性値データで要素数はデータ数に等しい

予測

テストデータの属性値の予測は、predict()メソッドにテストデータの特徴量を与える。

y = predict(X): Xはテストデータの特徴量データで、データ数×特徴量数の2次元配列。戻り値yは予測された属性値データで要素数はデータ数に等しい。

近傍点の情報

テストデータに対する近傍点の情報を、kneighbors()メソッドで得ることができる。

neigh_dist, neigh_ind = kneighbors(X): テストデータの特徴量Xを引数に与え、近傍点に関する情報を得る。neigh_distは各テストデータから各近傍点までの距離、neigh_indは各テストデータに対する各近傍点のインデックス。いずれも2次元の配列で、テストデータ数×近傍点数の2次元配列となっている。

実行例

以下の例では、n_neighbors=2としてKNeighborsRegressorのインスタンスを準備している。

これに対してfit()メソッドで、2つの特徴量とそれに対する属性値を持つ訓練データを5個与えている。特徴量データX_trainは行数がデータ数、列数が特徴量の数となる2次元配列を想定している。また属性値y_trainは訓練データ数と同じ要素数の1次元配列。

特徴量1	特徴量2	属性値
-2	-3	-1
-1	-1	0
0	1	1
1	2	2
3	3	3

これらの訓練データに対して、テストデータの特徴量X_testとして(-0.5, -2)、(1, 0)の2つを与えた時の出力を見てみる。

import numpy as np
from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(
    [[-2, -3],
     [-1, -1],
     [0, 1],
     [1, 2]])
y_train = np.array([-1, 0, 1, 2])

reg = KNeighborsRegressor(n_neighbors=2)
reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])
y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

print("X_train=\n{}".format(X_train))
print("y_train={}".format(y_train))
print("X_test=\n{}".format(X_test))
print("y_pred={}".format(y_pred))
print("neighbors' distance=\n{}".format(neigh_dist))
print("neighbors' indicies=\n{}".format(neigh_ind))

import numpy as np

from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(

[[-2, -3],

[-1, -1],

[0, 1],

[1, 2]])

y_train = np.array([-1, 0, 1, 2])

reg = KNeighborsRegressor(n_neighbors=2)

reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])

y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

print("X_train=\n{}".format(X_train))

print("y_train={}".format(y_train))

print("X_test=\n{}".format(X_test))

print("y_pred={}".format(y_pred))

print("neighbors' distance=\n{}".format(neigh_dist))

print("neighbors' indicies=\n{}".format(neigh_ind))

このコードの実行結果は以下の通り。

X_train=
[[-2 -3]
 [-1 -1]
 [ 0  1]
 [ 1  2]]
y_train=[-1  0  1  2]
[[-0.5 -2. ]
 [ 1.   0. ]]
y_pred=[-0.5  1.5]
neighbors' distance=
[[1.11803399 1.80277564]
 [1.41421356 2.        ]]
neighbors' indicies=
[[1 0]
 [2 3]]

X_train=

[[-2 -3]

[-1 -1]

[ 0 1]

[ 1 2]]

y_train=[-1 0 1 2]

[[-0.5 -2. ]

[ 1. 0. ]]

y_pred=[-0.5 1.5]

neighbors' distance=

[[1.11803399 1.80277564]

[1.41421356 2. ]]

neighbors' indicies=

[[1 0]

[2 3]]

属性値の予測結果については、2つのテストデータに対して2つの属性値0.5と1.5が返されている。

kneighbors()メソッドの戻り値から、1つ目のテストデータにはインデックスが1と0の2つの点とそれぞれへの距離1.118と1.802が、2つ目のテストデータにはインデックスが2と3の点とそれぞれへの距離1.414と2.0が得られる。

1つ目のテストデータ(-0.5, -2)からの距離
- X_train[1]=(-1, -1)→ $\sqrt{(-0.5)^2+1^2}\approx 1.118$
- X_train[0]=(-2, -3)→ $\sqrt{(-1.5)^2+(-1)^2}\approx 1.802$
2つ目のテストデータ(1, 0)からの距離
- X_train[2]=(0, 1)→ $\sqrt{(-1)^2+1^2}\approx 1.414$
- X_train[3]=(1, 2)→ $\sqrt{0^2+2^2}=2$

y_predは、テストデータごとに2つの近傍点の属性値の平均をとっている。

1つ目のテストデータの属性値
- y_train[1]=-1とy_train[0]=0の平均→-0.5
2つ目のテストデータの属性値
- y_train[2]=1とy_train[3]=2の平均→1.5

この様子を特徴量平面上に描いたのが以下の図である。各点の数値は、各データの属性値を示している。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(
    [[-2, -3],
     [-1, -1],
     [0, 1],
     [1, 2],
     [3, 3]])
y_train = np.array([-1, 0, 1, 2, 3])

reg = KNeighborsRegressor(n_neighbors=2)
reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])
y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

fig, ax = plt.subplots()

ax.scatter(X_train[:, 0], X_train[:, 1], label="X_train")
ax.scatter(X_test[:, 0], X_test[:, 1], marker='*', s=120, label="X_test")

for tests, ind in zip(X_test, neigh_ind):
    for neigh in ind:
        ax.plot(
            [tests[0], X_train[neigh][0]], [tests[1], X_train[neigh][1]],
            color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):
    ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))
for x, y in zip(X_test, y_pred):
    ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

ax.set_xlabel("feature 1")
ax.set_ylabel("feature 2")
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(

[[-2, -3],

[-1, -1],

[0, 1],

[1, 2],

[3, 3]])

y_train = np.array([-1, 0, 1, 2, 3])

reg = KNeighborsRegressor(n_neighbors=2)

reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])

y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

fig, ax = plt.subplots()

ax.scatter(X_train[:, 0], X_train[:, 1], label="X_train")

ax.scatter(X_test[:, 0], X_test[:, 1], marker='*', s=120, label="X_test")

for tests, ind in zip(X_test, neigh_ind):

for neigh in ind:

ax.plot(

[tests[0], X_train[neigh][0]], [tests[1], X_train[neigh][1]],

color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):

ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

for x, y in zip(X_test, y_pred):

ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

ax.set_xlabel("feature 1")

ax.set_ylabel("feature 2")

ax.legend()

plt.show()

各種データに対する適用例

waveデータ

waveデータセット

2020-03-21 / tau / コメントする

概要

waveデータセットは、”Pythonではじめる機械学習”(O’REILLY)中で用いられる架空のデータセットである。

その内容は、引数n_samplesで指定した個数の点について1つの特徴量とターゲットの値を持ち、回帰を扱うのに適している。

利用方法

mglearnパッケージから、たとえば以下のように利用する。

from mglearn.datasets import make_wave

X, y = make_wave(n_samples=40)

from mglearn.datasets import make_wave

X, y = make_wave(n_samples=40)

実行するとdeprecatedの警告が出るが、放置してもよいらしい。

内容

waveデータの特徴は以下の通り。

引数のn_samplesには任意の整数を指定できる
特徴量（x座標の値）は決まっている
- n_samplesが増えてもx₀, x₁, …の値は変わらない
- x₀, x₁, …は実行のたびに同じパターン
ターゲットの値（y座標の値）は変化するが実行ごとに同じ
- n_samplesが変わると同じx₀, x₁, …の値に対するy₀, y₁, …の値は変化する
- y₀, y₁, …は実行のたびに同じパターン

このことを、n_samplesの値を変化させたときのX, yの内容で確認してみる。

import matplotlib.pyplot as plt
from mglearn.datasets import make_wave

n_samples_list = [1, 2, 3, 4, 5, 6]

for n_samples in n_samples_list:
    X, y = make_wave(n_samples=n_samples)
    print("\nn_samples={}".format(n_samples))
    for u, v in zip(X, y):
        print("({:6.3f}, {:6.3f})".format(u[0], v))

# n_samples=1
# (-0.7528, -0.9974)
# 
# n_samples=2
# (-0.7528, -0.1176)
# ( 2.7043,  1.6216)
# 
# n_samples=3
# (-0.7528, -0.9974)
# ( 2.7043,  1.0195)
# ( 1.3920,  0.5076)
# 
# n_samples=4
# (-0.7528, -0.5585)
# ( 2.7043,  0.7430)
# ( 1.3920,  1.1577)
# ( 0.5920,  1.0291)
# 
# n_samples=5
# (-0.7528, -0.3020)
# ( 2.7043,  1.3653)
# ( 1.3920,  0.0776)
# ( 0.5920,  0.3828)
# (-2.0639, -1.7779)
# 
# n_samples=6
# (-0.7528,  0.3481)
# ( 2.7043,  1.2438)
# ( 1.3920,  0.1333)
# ( 0.5920,  0.9167)
# (-2.0639, -1.7239)
# (-2.0640, -1.7250)

import matplotlib.pyplot as plt

from mglearn.datasets import make_wave

n_samples_list = [1, 2, 3, 4, 5, 6]

for n_samples in n_samples_list:

X, y = make_wave(n_samples=n_samples)

print("\nn_samples={}".format(n_samples))

for u, v in zip(X, y):

print("({:6.3f}, {:6.3f})".format(u[0], v))

# n_samples=1

# (-0.7528, -0.9974)

# n_samples=2

# (-0.7528, -0.1176)

# ( 2.7043, 1.6216)

# n_samples=3

# (-0.7528, -0.9974)

# ( 2.7043, 1.0195)

# ( 1.3920, 0.5076)

# n_samples=4

# (-0.7528, -0.5585)

# ( 2.7043, 0.7430)

# ( 1.3920, 1.1577)

# ( 0.5920, 1.0291)

# n_samples=5

# (-0.7528, -0.3020)

# ( 2.7043, 1.3653)

# ( 1.3920, 0.0776)

# ( 0.5920, 0.3828)

# (-2.0639, -1.7779)

# n_samples=6

# (-0.7528, 0.3481)

# ( 2.7043, 1.2438)

# ( 1.3920, 0.1333)

# ( 0.5920, 0.9167)

# (-2.0639, -1.7239)

# (-2.0640, -1.7250)

このコードは何度実行しても同じ値を返す。x座標のパターンが変わっていないこと、y座標のパターンは実行のたびに変化していることがわかる。ただし異なるn_sampleに対して、同じxに対するyの値は大きくは変化していない。

なお、n_samplesが6の時のxの最後の値とその1つ前の値がかなり近く、対応するyの値も近い。n_samplesが1の時と3の時に、先頭のXとyの値が殆ど等しい。

以上のことから、waveデータセットはXについては毎回同じ系列でランダムな値を返し、yはXに対して一定の計算値に毎回同じ系列の乱数で擾乱を加えていると想像される。

最後に、n_samplesを多くしたときの結果を見てみると明らかに線形で上昇しつつ波打っているのがわかる。おそらく $y=a \sin b x + c$ のような式に擾乱を与えていると思われる。

手法の適用

最近傍回帰(knn)

Breast cancer データセット – k-近傍法

2020-03-20 / tau / コメントする

概要

breast_cancerデータセットにscikit-learnのKNeighborsClassifierクラスでk-最近傍法を適用した結果。

学習率曲線

breast_cancerデータセットにk-最近傍法を適用し、近傍点数を変化させて学習率の変化をチェック。データセットを学習データとテストデータに分けるときのrandom_stateを変え、近傍点数に伴う変化を見てみた。

irisデータセットの場合に比べると、学習データとテストデータの傾向は落ち着いていて、近傍点数=8で制度が0.92～0.95程度。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


def train_and_test(X, y, n_neighbors_list, random_state):

    X_train, X_test, y_train, y_test =\
        train_test_split(X, y, stratify=y, random_state=random_state)

    training_scores = []
    test_scores = []

    for n_neighbors in n_neighbors_list:
        classifier = KNeighborsClassifier(n_neighbors=n_neighbors)

        classifier.fit(X_train, y_train)

        training_scores.append(classifier.score(X_train, y_train))
        test_scores.append(classifier.score(X_test, y_test))

    return training_scores, test_scores


cancer_ds = load_breast_cancer()
X = cancer_ds.data
y = cancer_ds.target

n_neighbors_list = np.arange(1, 16, dtype=int)
random_state_list = np.array([0, 1, 2, 3])

fig, axs = plt.subplots(2, 2, figsize=(9.6, 7.2))
plt.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)[0]

# random_stateを変化させて学習率の違いを見る
for ax, random_state in zip(axs_1d, random_state_list):
    training_scores, test_scores =\
        train_and_test(X, y, n_neighbors_list, random_state)

    ax.plot(n_neighbors_list, training_scores)
    ax.plot(n_neighbors_list, test_scores)

    ax.set_title("random_state={}".format(random_state))
    ax.set_xlabel("number of neighbors")
    ax.set_ylim(0.9, 1.01)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsClassifier

def train_and_test(X, y, n_neighbors_list, random_state):

X_train, X_test, y_train, y_test =\

train_test_split(X, y, stratify=y, random_state=random_state)

training_scores = []

test_scores = []

for n_neighbors in n_neighbors_list:

classifier = KNeighborsClassifier(n_neighbors=n_neighbors)

classifier.fit(X_train, y_train)

training_scores.append(classifier.score(X_train, y_train))

test_scores.append(classifier.score(X_test, y_test))

return training_scores, test_scores

cancer_ds = load_breast_cancer()

X = cancer_ds.data

y = cancer_ds.target

n_neighbors_list = np.arange(1, 16, dtype=int)

random_state_list = np.array([0, 1, 2, 3])

fig, axs = plt.subplots(2, 2, figsize=(9.6, 7.2))

plt.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)[0]

# random_stateを変化させて学習率の違いを見る

for ax, random_state in zip(axs_1d, random_state_list):

training_scores, test_scores =\

train_and_test(X, y, n_neighbors_list, random_state)

ax.plot(n_neighbors_list, training_scores)

ax.plot(n_neighbors_list, test_scores)

ax.set_title("random_state={}".format(random_state))

ax.set_xlabel("number of neighbors")

ax.set_ylim(0.9, 1.01)

plt.show()

概要

各特徴量の分布

各特徴量と価格の関係

2つの特徴量と価格の関係

概要

データの取得とデータ構造

データの内容

'data'～特徴量データセット

'target'～住宅価格

'feature_names'～特徴名

'filename'～ファイル名

'DESCR'～データセットの説明

データの利用

データの取得方法

全レコードの特徴量データの取得

特定の特徴量のデータのみ取得

概要

近傍点数とクラス分類の挙動

近傍点数=1の場合

近傍点数=2の場合

近傍点数=3の場合

実行コード

knnの精度

予測カーブ

訓練データが少ない場合

訓練データが多い場合

概要

近傍点数によるクラス分類の挙動

近傍点数=1の場合

近傍点数=3の場合

近傍点数=2の場合

決定境界

概要

利用方法

手順

パッケージのインポート

コンストラクター

訓練

予測

近傍点の情報

実行例

各種データに対する適用例

概要

利用方法

内容

手法の適用

概要

学習率曲線

`'data'`～特徴量データセット

`'target'`～住宅価格

`'feature_names'`～特徴名

`'filename'`～ファイル名

`'DESCR'`～データセットの説明