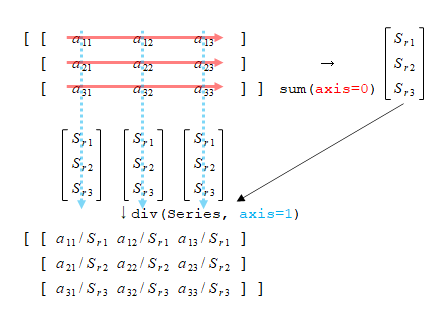
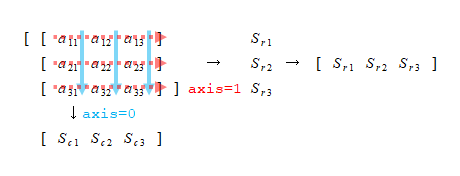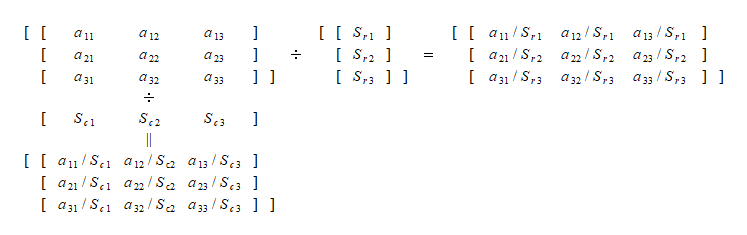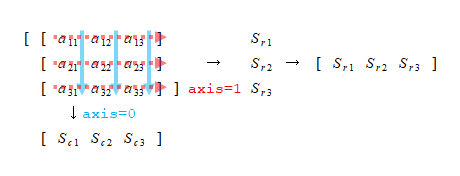概要
scikit-learnの主成分分析モデル(PCA)をBreast cancerデータセットに適用して、その挙動を確認する。
30個の特徴量(全て連続量)を持つ569個の腫瘍データについて、悪性(marignant)/良性(benign)がターゲットとして与えられている。PCAによって特徴量のみの分析で、少ない主成分によってある程度明確な分離が可能なことが示される。
手順
以下の手順・コードで計算した。
- パッケージをインポート
- Breast cancerデータセットを準備
- データセットをスケーリング
StandardScalerで特徴量データを標準化している
- PCAモデルのインスタンスを生成
- 引数
n_components=3で3つの主成分まで計算させている
- 引数
fit()メソッドによって、モデルにデータを学習させる- 成分やその寄与率を確認
- 主成分は
PCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
- 主成分は
transform()メソッドによって、主成分に沿ってデータを変換- 3つの主成分について3次元可視化
- 2つの主成分について2次元可視化
主成分と寄与率
以下に主成分と寄与率を計算するまでのコードを示す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_breast_cancer from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from mpl_toolkits.mplot3d import Axes3D ds = load_breast_cancer() X_scaled = StandardScaler().fit_transform(ds.data) df = pd.DataFrame(X_scaled, columns=ds.feature_names) pca = PCA(n_components=3) pca.fit(df) print("Components:\n{}".format(pca.components_)) # Components: # [[ 0.21890244 0.10372458 0.22753729 0.22099499 0.14258969 0.23928535 # 0.25840048 0.26085376 0.13816696 0.06436335 0.20597878 0.01742803 # 0.21132592 0.20286964 0.01453145 0.17039345 0.15358979 0.1834174 # 0.04249842 0.10256832 0.22799663 0.10446933 0.23663968 0.22487053 # 0.12795256 0.21009588 0.22876753 0.25088597 0.12290456 0.13178394] # [-0.23385714 -0.0597061 -0.21518137 -0.23107672 0.18611299 0.15189161 # 0.06016536 -0.03476749 0.19034877 0.36657548 -0.10555215 0.0899797 # -0.08945723 -0.15229263 0.20443047 0.23271588 0.19720726 0.13032158 # 0.18384799 0.28009201 -0.21986638 -0.0454673 -0.19987843 -0.21935186 # 0.17230435 0.14359318 0.09796412 -0.00825721 0.14188335 0.27533948] # [-0.00853135 0.06454967 -0.00931432 0.02869944 -0.10429256 -0.07409161 # 0.00273383 -0.0255634 -0.0402399 -0.02257393 0.26848142 0.37463394 # 0.26664551 0.21600645 0.30883931 0.15477941 0.17646341 0.22465797 # 0.28858416 0.21150348 -0.04750699 -0.0422979 -0.04854648 -0.0119023 # -0.25979771 -0.23607553 -0.17305727 -0.17034366 -0.27131257 -0.23279102]] print("Explained :{}".format(pca.explained_variance_ratio_)) # Explained :[0.44272026 0.18971182 0.09393163] |
寄与率は第1主成分が44%、第2主成分が19%、第3主成分が9%。第3成分まで3/4の情報を説明していることになる。
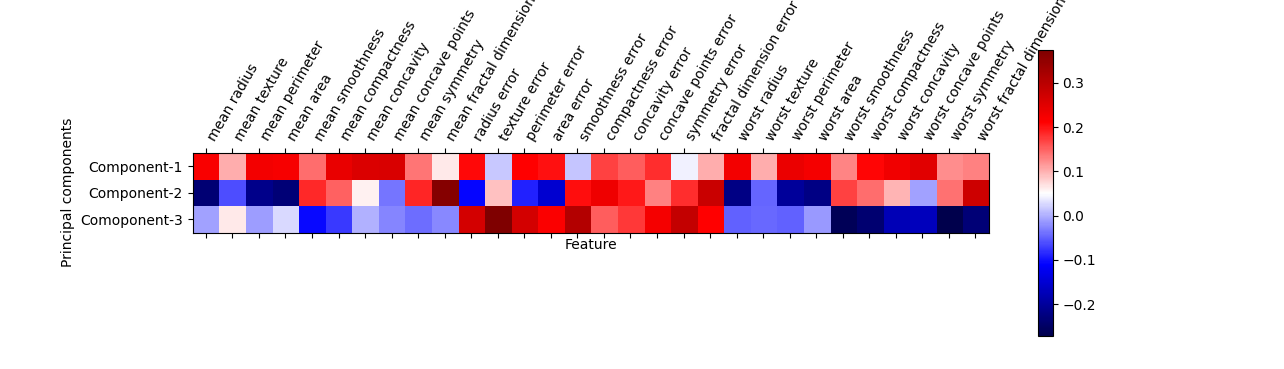
また、第1主成分は全ての特徴量がプラス方向で寄与している。
主成分をヒートマップで視覚化してみると、各主成分の符号や大きさが直感的に把握しやすくなるが、第2~第3主成分がmeanとworst系の特徴量が小さい方が影響が大きい点、3つの主成分についてerrorが大きいほど影響が大きい点など、意味づけは難しい。
|
1 2 3 4 5 6 7 8 9 |
plt.matshow(pca.components_, cmap='seismic') plt.yticks([0, 1, 2], ["Component-1", "Component-2", "Comoponent-3"]) plt.colorbar() plt.xticks(range(len(ds.feature_names)), ds.feature_names, rotation=60, ha='left') plt.xlabel("Feature") plt.ylabel("Principal components") plt.show() |
可視化
3次元
3つの主成分について3次元で可視化してみると、悪性/良性がかなりはっきりと分離されている。
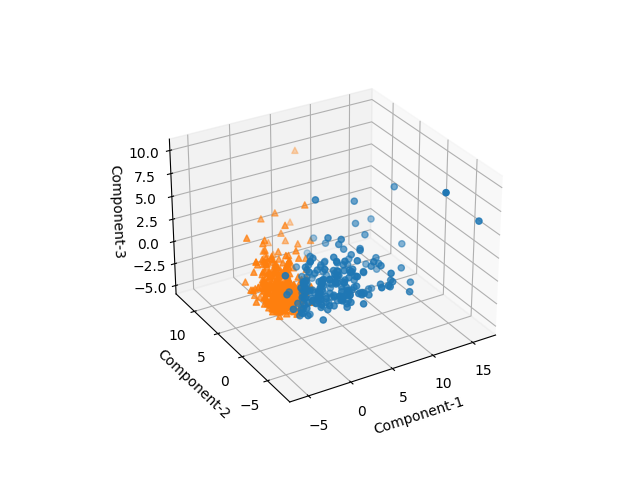
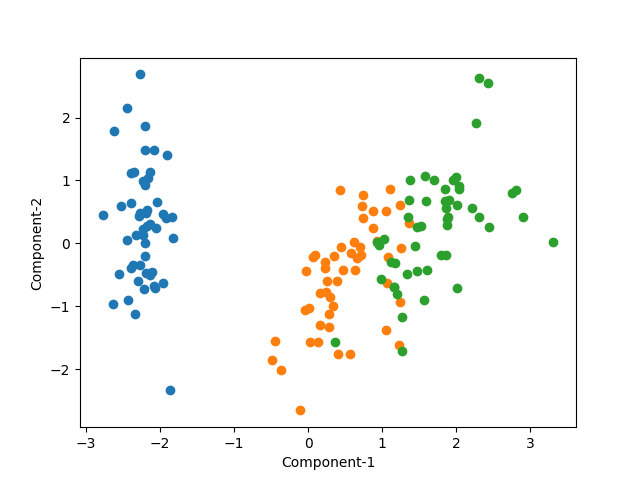
2次元
2つの主成分のみでも、悪性/良性がよく区分されている。
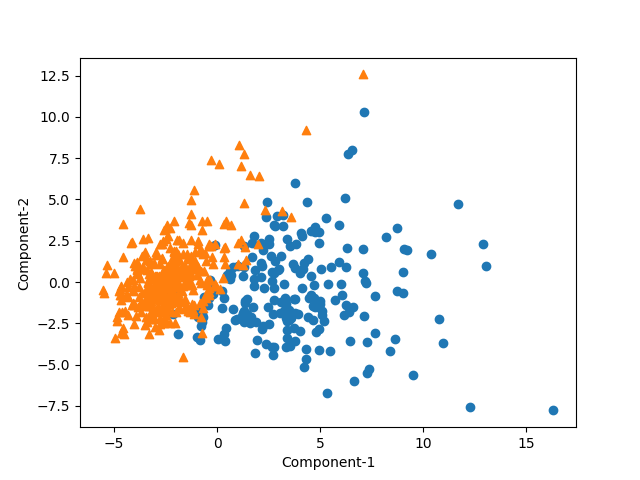
まとめ
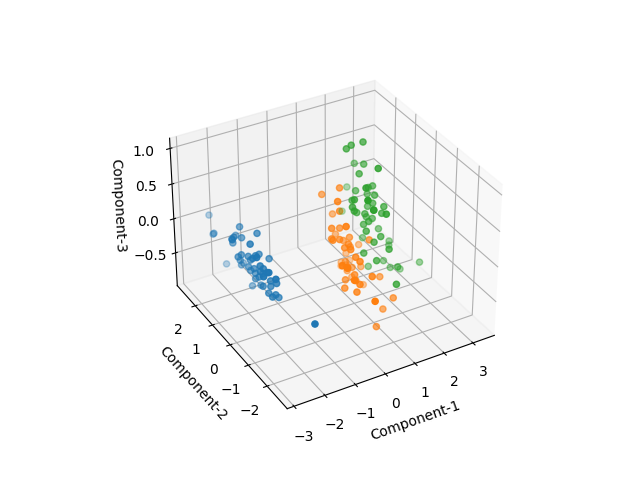
Irisデータの場合と同じく、特徴量分析のみでクラスの別がよくあぶりだされている。
![Rendered by QuickLaTeX.com \begin{align*} E(x_{i | \boldsymbol{d}} ) &= E\left[ (d1, d2) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) \right] = (d_1, d_2) \left( \begin{array}{c} E(x_{i1}) \\ E(x_{i2}) \end{array} \right) \\ &= (d_1, d_2) \left( \begin{array}{c} \mu_{i1} \\ \mu_{i2} \end{aray} \right) \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-6d6230f138fc3fa7ed12c321cb886709_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} V( x_{i | \boldsymbol{d}} ) &= V \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \\ &= E \left[ \left( \boldsymbol{d}^T \boldsymbol{x}_i - E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \right)^2 \right] \\ &= E \left[ \left( {\boldsymbol{d}}^T \left( \boldsymbol{x}_i - E(\boldsymbol{x}_i) \right) \right)^2 \right] \\ &= E \left[ {\boldsymbol{d}}^T (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \boldsymbol{d} \right] \\ &= \boldsymbol{d}^T E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \boldsymbol{d} \\ &= \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-124a18127aad98b510df2af2181173ee_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \\ &= E \left[ \left( \begin{array}{c} x_{i1} - \mu_1 \\ x_{i2} - \mu_2 \end{array} \right) (x_{i1} - \mu_1, x_{i2} - \mu_2) \right] \\ &= \left[ \begin{array}{cc} (x_{i1} - \mu_1)^2 & (x_{i1} - \mu_1)(x_{i2} - \mu_2) \\ (x_{i2} - \mu_2)(x_{i1} - \mu_1) & (x_{i2} - \mu_2)^2 \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-6f7b889cad8cd2284e27cc9de5f9ede2_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \tt{components\_} = \left[ \begin{array}{ccc} (p_{0, 0} & \cdots & p_{0, n-1} ) \\ & \vdots &\\ (p_{m-1, 0} & \cdots & p_{m-1, n-1}) \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{p}_0 \\ \vdots \\ \boldsymbol{p}_m \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d9be42d7f003af87c8a132ea3f54bba8_l3.png)