記号定義
以降の議論で以下の様に記号を定義する。
- 変数Aの否定(not)→
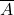
- 変数AとBの論理積(and)→
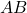 または
または
- 変数AとBの論理和(or)→
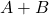
- 変数AとBの吐いた論理和(xor)→
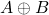
基本演算の真理値表
not/and/or
not、and、orの真理値表は以下のとおり。T、FはTrue(真)、False(偽)を表す。
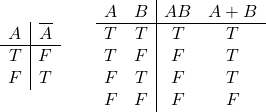
排他論理和(exclusive or)
2つの変数の真偽値が「異なるときに真、同じ時に偽」となる演算。
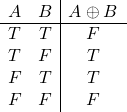
各種法則
基本
(1) 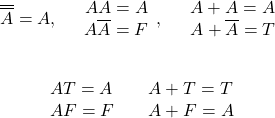
交換法則
(2) ![]()
結合法則
(3) ![]()
<確認>

分配法則
(4) ![]()
<確認>

ド・モルガンの法則(De Morgan’s laws)
ド・モルガンの法則はandとorの相互変換に関するもので、論理式の変形の基本手順として使われる。
(5) ![]()
<確認>
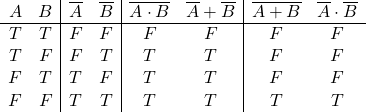
ド・モルガンの法則による式変形
変形の基本
ド・モルガンの法則を利用して論理式を変形していくのに、以下の変形手順が用いられる。
<否定の否定>
(6) ![]()
<Falseとのor>
(7) ![]()
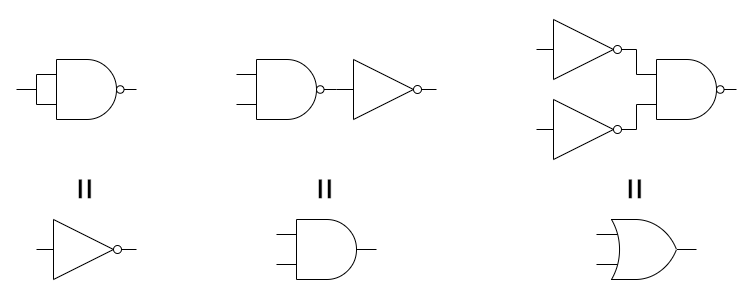
NANDゲート化
NANDゲートは、A、B2つの入力のandのnotを出力するゲートで、任意の論理回路をNANDゲートの組み合わせで実装できる(完全性:completeness)。
例えばnot、and、or、xorの基本演算を、ド・モルガンの低利で変形してNANDゲートのみで表してみる。
(8) 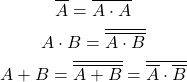
これらをゲート図で表すと以下のようになる。
真偽表の変換
変換の考え方
排他論理和(XOR)の演算をNANDゲートで構成することを考える。AとBに対するTrue、Falseの組み合わせのうち結果がTrueとなるものだけを抜き出すと、(A, B) = (T, F), (F, T)。それぞれの入力に対して結果がTrueとなるためには以下のいずれか満たされる必要がある。
(9) ![]()
これらのいずれかが成立すれば(左辺の論理和を取れば)Trueの結果となり、Falseとなる結果は論理和をとっても変わらないので、XORの出力は以下のように表現される。
(10) ![]()
この式に真偽値表の組み合わせを入れると、XORの結果になることが確認できる。
NANDゲートへの変換1
この式をド・モルガンの定理を使って変形すると以下のようになる。
(11) 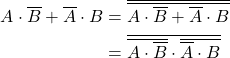
真理値表の確認。
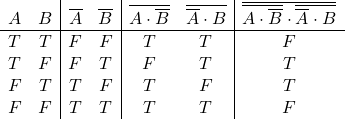
式(11)をNANDゲートによる回路図で表すと以下の通り。2つのNOTはNANDゲートで作ることができ、5つのNANDゲートを使う。
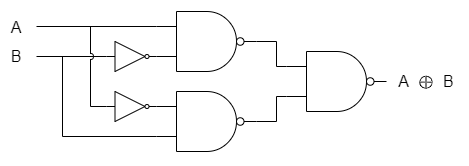
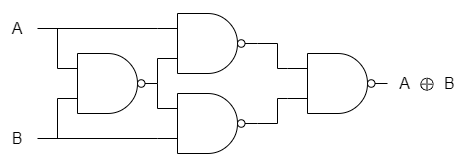
NANDゲートへの変換2
一方、式(11)の2つのNANDの中を以下のように変形する。
(12) ![]()
これらにより、XORは以下のようにも表せる。
(13) 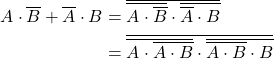
式(12)をNANDゲートによる回路図で表すと以下の通り。式(11)の場合に比べてNANDゲートが4つですむ。