月別: 2023年6月

ロジスティック関数

/ tau / コメントする

増加率一定

個体の増加速度が個体数に比例する場合、以下のような方程式になる。

(1)   \begin{equation*} \frac{dN}{dt} =m N \end{equation*}

この解は以下のような指数関数となり、ある程度以上から先は急激に個体が増加し、無限に増えていく。

(2)   \begin{equation*} N(t) = N_0 e^{mt} \end{equation*}

ロジスティック関数～増加に対する歯止め

増加率を一定ではなく個体数Nに応じた値となるよう、以下の関数とする。

(3)   \begin{equation*} m(N) = r \left( 1 - \frac{N}{K} \right) \end{equation*}

個体数が増えるにしたがって増加率は減少し、個体数がKのときに増加率はゼロ、それよりも多いときには個体数は減少する。

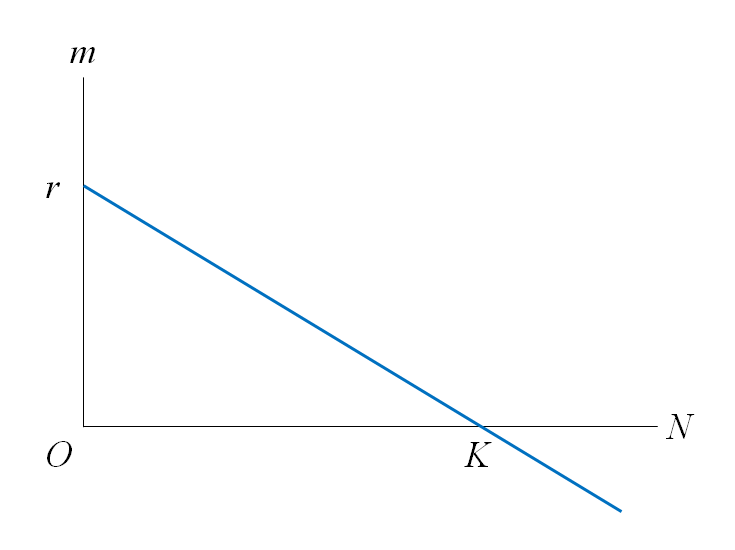
この増加率を適用した微分方程式は以下の通り。

(4)   \begin{equation*} \frac{dN}{dt} = r \left( 1 - \frac{N}{K} \right) N \end{equation*}

まず以下のように変形。

(5)   \begin{equation*} \frac{dN}{dt} = \frac{r}{K} (K - N) N \end{equation*}

変数分離形。

(6)   \begin{equation*} \frac{K}{(K - N) N} dN = r dt \end{equation*}

分数部分を以下のように変形。

(7)   \begin{equation*} \left( \frac{1}{N} - \frac{1}{K - N} \right) dN = r dt \end{equation*}

積分した一般解は以下の通り。

(8)   \begin{equation*} \ln N - \ln (K-N) = rt + const. \end{equation*}

指数関数の形に。

(9)   \begin{equation*} \frac{N}{K - N} = A e^{rt} \end{equation*}

Nをまとめる。

(10)   \begin{equation*} \frac{K - N}{N} = \frac{K}{N} - 1 = A e^{-rt} \end{equation*}

Nについて解いた一般解を得る。

(11)   \begin{equation*} N = \frac{K}{1 + A e^{-rt}} \end{equation*}

これにt=0のときの初期値N0を適用して、以下の解を得る。

(12)   \begin{equation*} N = \frac{K}{ 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} } \end{equation*}

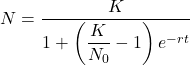
t=0のときは初期値N0、t→∞のときはN=Kに収束する。

(13)   \begin{equation*} \left\{ \begin{array}{l} N(0) = N_0 \\ \lim\limits_{t \to \infty} N(t) = K \end{array} \end{equation*}

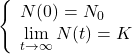
N0=2, r=10, K=1000のグラフを描くと以下の通り。

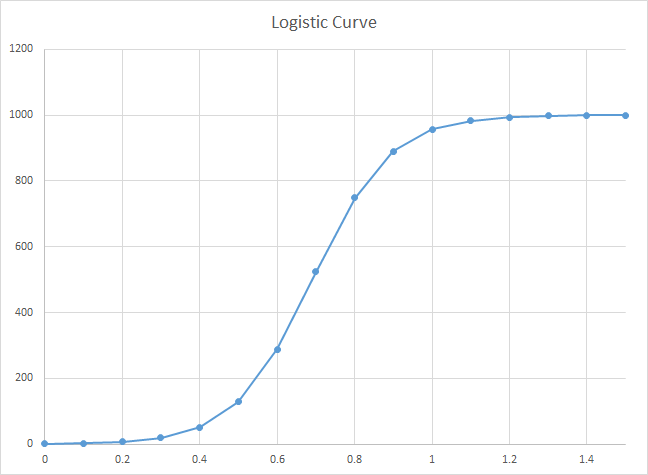
また先の解を微分して増加速度の式を求めると以下の様になる。

パラメーターの影響

初期値N0

  1. 初期値がKより小さいときはよく見られるロジスティック曲線でKに漸近する
  2. Kと等しいときは変化しない
  3. Kより大きいときは指数関数的にKに漸近する

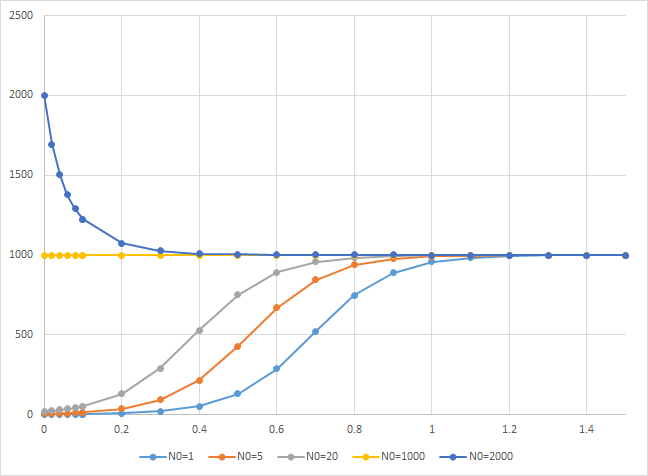
増加率r

増加率が大きいほど立ち上がりが急になり、小さいほど緩やかになる。

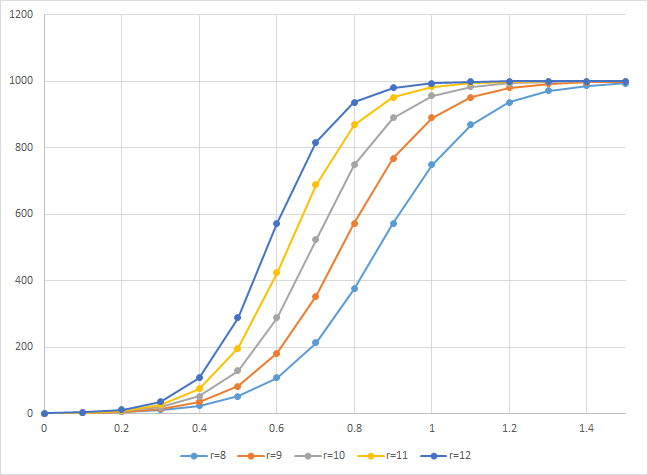
収束値K

収束値Kに向かって漸近する。

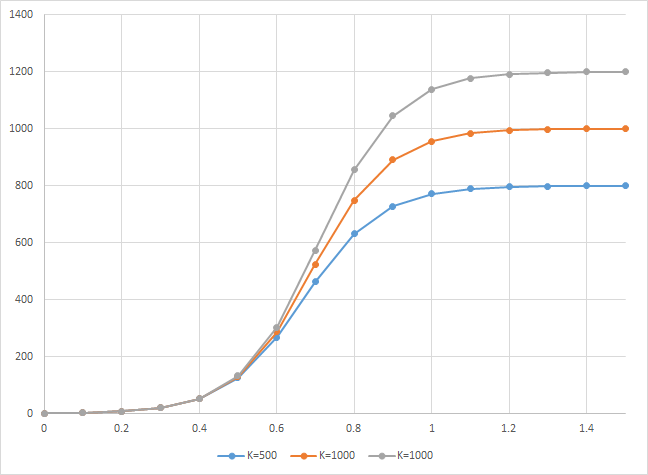
増加速度

Nをtで微分して増加速度の式を得る。

(14)   \begin{equation*} \frac{dN}{dt} = r \frac{\left( \dfrac{K}{N_0} - 1 \right) e^{-rt}}{\left( 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} \right)^2} \end{equation*}

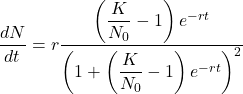
増加速度のグラフは以下の様になり、極大値を一つ持つ。

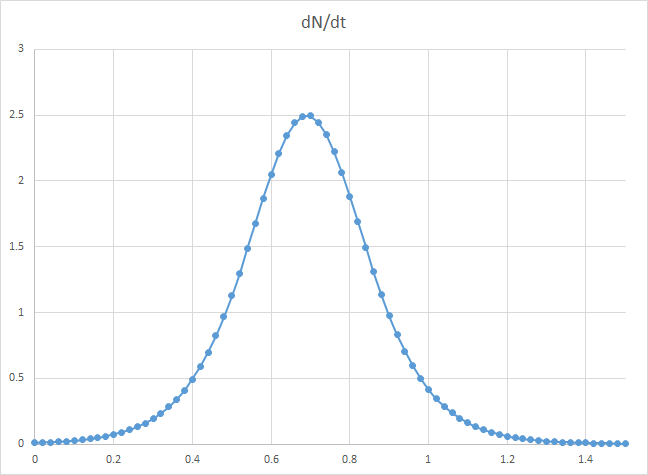
増加速度が最大となるtの値は、K/N0 – 1 = Cとおいて以下の様に得られる。

(15)   \begin{equation*} t = \frac{1}{r} \ln C = \frac{1}{r} \ln \left( \frac{K}{N_0} - 1 \right) \end{equation*}

これは以下の様にしても導ける。式(4)の値がゼロとなるのはN=K/2のときなので、これを式(12)に代入して、

(16)   \begin{equation*} 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} = 2 \end{equation*}

これを解いて(15)と同じ解を得る。