コイル（インダクター）

/ tau / コメントする

電流・磁界の法則

右ネジの法則

電流が流れると、その方向に対して右回りの磁界が発生する（Maxwell’s right-handed screw rule）。

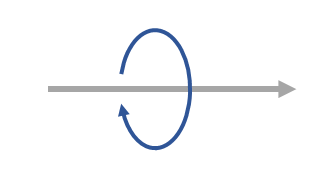
右手の法則

コイルに電流を流すと、電流の向きが右手を握った各指の方向のとき親指の挿す方向に磁界が発生する。

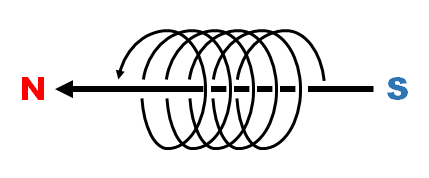
フレミングの左手／右手の法則

絵は面倒なので割愛。人差し指が磁界、中指が電流、親指が力の方向。左手は磁界内の電流に働く力、右手は磁界内で運動する場合に発生する電流の方向。

ローレンツ力

電荷e[C]の荷電粒子が磁束密度B[T]内を運動ベクトルvで移動するとき、荷電粒子に対してフレミングの左手の法則に従って力が働く。

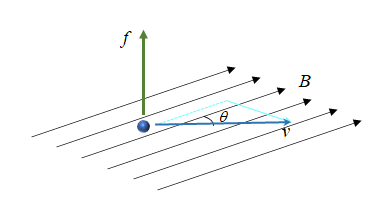
このとき、vが磁束に対してなす角をθとすると、荷電粒子に働く力は以下の様になる。

(1)   \begin{equation*} f = q v (\sin \theta) B \end{equation*}

ローレンツ力の方向まで含める場合、ベクトルの外積よって以下の様に表せる。

(2)   \begin{equation*} \boldsymbol{f} = q \boldsymbol{v} \times \boldsymbol{B} \end{equation*}

レンツの法則

コイルを通る磁束が変化するとき、その磁束の変化を妨げる方向に誘導電流が生じる。

たとえば以下の図では、コイルに対して磁石のN極側を近づけている。このときコイルに対して左から右へ向かう磁束が増加するので、それ打ち消す右から左の磁束を増やすように誘導電流が流れる。

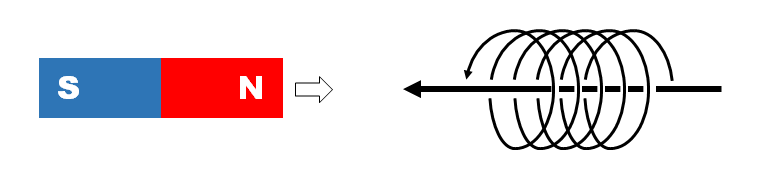
この状態で磁石が離れていくときは右向きの磁束が減少するので、コイル内で同じ右向きの磁束を発生させるよう、上図と逆向きの電流が流れる。

一方、S極が近づくときは左向きの磁束が増えるので、これと逆の右向きの磁束が発生するよう、上図と逆向きの電流が流れる。

S極が離れる場合には、左向きの磁束が減少するので、これを補うように左向きの磁束を発生させる方向（上図と同じ方向）に電流が流れる。

ファラデーの法則

閉回路を貫く磁束Φが変化するとき、レンツの法則によりその変化を妨げる方向の電流が流れるが、この起電力を誘導起電力という。誘導起電力の大きさは以下のように表される。

(3)   \begin{equation*} | V | = \left| \frac{d \Phi}{dt} \right| \end{equation*}

起電力の正負の向きについて、「磁束の変化を妨げるように」というレンツの法則から、以下の様に表現される。

(4)   \begin{equation*} V = - \frac{d \Phi}{dt} \end{equation*}

またコイルの巻き数がNのときは、以下の様になる。

(5)   \begin{equation*} V = - N \frac{d \Phi}{dt} \end{equation*}

コイルの自己誘導

自己誘導とは

コイルにかかる電圧が変化した場合場合、電流の変化に応じて磁界が変化するが、レンツの法則によってそれを阻止しようとする方向の電流を流そうという起電力も生じる。このような現象をコイルの自己誘導と言い、自己誘導によって生じる元の電圧と逆の起電力を逆起電力という。

電源が立ち上がった場合

たとえば以下のような回路を考える。ここで電源電圧が0→Eに立ち上がった場合、コイルによる逆起電力、抵抗による電圧降下が生じる。電源の起電力は正極側を⊕としている。抵抗Rの電圧は電源に対して電圧降下となる電流の向きの矢印、コイルの方は電流の変化によるので両方向きの矢印としている。

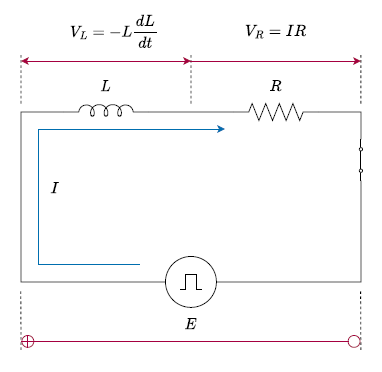
電流をI = I(t)として、電圧のバランスを定式化すると、以下のようになる。

(6)   \begin{equation*} E - L \frac{dI}{dt} - RI = 0 \end{equation*}

この微分方程式を以下のように解いていく。

(7)   \begin{equation*} \frac{dI}{E - RI} = \frac{dt}{L} \end{equation*}

(8)   \begin{equation*} -\frac{1}{R} \ln (E - RI) = \frac{t}{L} + const \end{equation*}

(9)   \begin{equation*} I = \frac{E - k e^{- \frac{R}{L} t}}{R} \end{equation*}

ここでIt=0 = 0の条件によりkを決定する。

(10)   \begin{equation*} \frac{E - k}{R} = 0 \quad \Rightarrow \quad k = E \end{equation*}

よって、自己誘導を含めた電流変化は以下のように求められる。

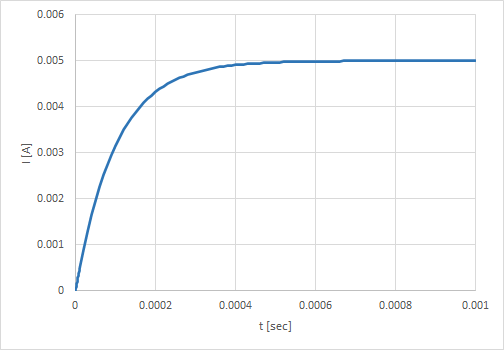
(11)   \begin{equation*} I = \frac{E}{R} \left(1 - e^{- \frac{R}{L} t} \right) \end{equation*}

以下のグラフは、L = 100mH、R = 1kΩ、E = 5Vの場合にスイッチON以降の電流変化を計算したもの。自己誘導の影響がなくなり定常電圧になるのに500μsほどかかっている。

電圧が立ち下がった場合

初期電流It=0 = E/Rとして、t = 0でE = 0になったとして先の微分方程式を解いてみる。まず式(6)でE = 0と置く

(12)   \begin{equation*} - L \frac{dI}{dt} - RI = 0 \end{equation*}

これを解いて

(13)   \begin{equation*} I = k e^{- \frac{R}{L} t} \end{equation*}

初期条件を考慮して以下を得る。

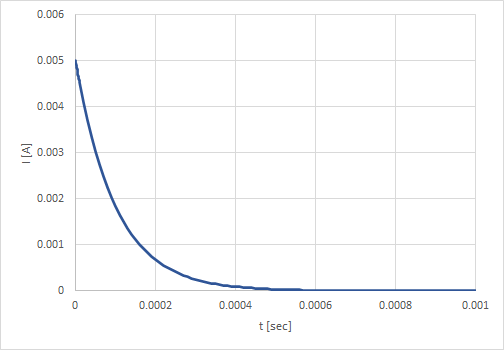
(14)   \begin{equation*} I = \frac{E}{R} e^{- \frac{R}{L} t} \end{equation*}

この式形は式(11)と上下逆の形になっていて、以下のようなグラフになる。

サージ

サージの考え方？

コイルを含む回路を半導体素子で開閉した場合、スイッチOFFの際に高電圧のサージが発生するということを知った。ただし定性的な（あるいは感覚的な）原理は多くみられるが、そのメカニズムがどうも腹に落ちない。

「スイッチOFFにしても電流が流れようとするので誘導起電力が発生し・・・」という説明を見かけるが、もし理想的なスイッチで瞬間的にOFFとなるなら、誘導電流が流れる時間がゼロだから、回路としてはそのまま黙ってしまうのではないか（dI/dtが無限大になるのとどう関係するのか定かではないが）。

スイッチが完全にOFFになるまでに若干のスパークが発生することや、スイッチング阻止の抵抗が無限大ではないことを含めて説明している場合もあり、これは現実論として納得できる。

特にこちらのサイトはとても参考になったので、これを自分なりにトレースして、理解を試みた。

まず以下の図で、電源Eに接続していた状態からスイッチを抵抗S側に切り替えたとする。ただし以下の点に留意する。

  • 切り替え前は定常状態で、回路の電流はI = E/R
  • ここでのスイッチは理想的なスイッチとし、抵抗Sが現実のスイッチ切り替え時の抵抗に相当

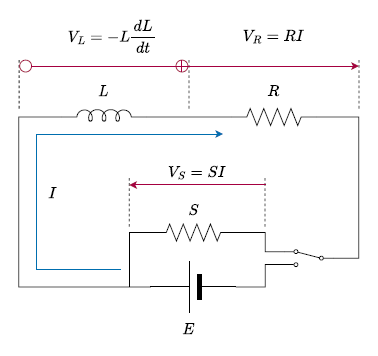
ここで切り替えの瞬間をt = 0として微分方程式は以下のようになる。

(15)   \begin{equation*} - L \frac{dI}{dt} - RI - SI = 0 \end{equation*}

初期条件t = 0でI = E/Rとして解いて、以下を得る。

(16)   \begin{equation*} I = \frac{E}{R} e^{- \frac{R + S}{L}t} \end{equation*}

この電流に対してコイルは起電側となり、2つの抵抗で電圧降下となって、それらは以下のようになる。

(17)   \begin{equation*} \left\{ \begin{array}{l} V_R = RI = E e^{- \frac{R + S}{L}t} \\ V_S = SI = \dfrac{S}{R} E e^{- \frac{R + S}{L}t} \\ V_L = - L \dfrac{dI}{dt} = - \dfrac{R + S}{R} E e^{- \frac{R + S}{L}t} \end{array} \end{equation*}

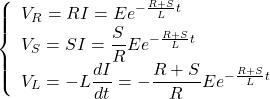
この式によるなら、t=0でコイルによる起電力は(R + S)/Rとなり、このうちS/Rが抵抗Sの電圧降下となる。たとえばR=1kΩのときにSが10kΩでも元の電源電圧の10倍の電圧がSの両端にかかることになる。

この様子を先と同じ条件L = 100mH、R = 1kΩ、E = 5Vに加えてS = 10kΩとして描いたのが以下のグラフ。スイッチOFFのときにEの10倍の50Vが生じ、そこから急激に電圧が下がっている。また時定数(R + S)/Rも大きくなるので、減少の時間も1オーダー短くなっている。

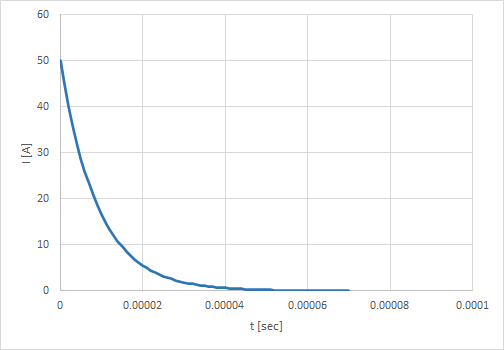
このSが大きくなると、その倍率に応じて大きな電圧が生じ、低減時間は短くなる。すなわち、一瞬の間だけ高電圧が発生する。これがコイルによるサージと呼ばれるものではないか。

ただし元々接続されていたRの両端の電圧の最大値は変わらないので、サージの影響を受けるのはスイッチ素子ということになる。ここにトランジスターなどを使っていると、たとえばC–E間に逆向きの高電圧がかかって破壊されてしまう。

保護回路

コイルサージから回路を保護するためにいろいろあるようだが、最も簡単なのは以下の様にダイオードを加えることらしい。

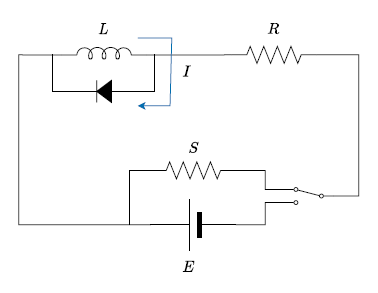
通常のスイッチONの状態ではダイオードが逆向きなのでコイルに電流が流れ、サージ電流はダイオードを通じて戻るので、RやSには影響を与えない。

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です