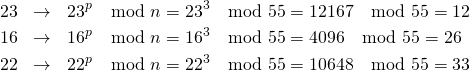公開鍵と秘密鍵

/ tau / コメントする

暗号化

暗号化の流れ

公開鍵(public key)と秘密鍵(secret/private key)を使った暗号化の流れは以下のとおり。

  1. 受信側が公開鍵と秘密鍵を準備し、公開鍵を公開
  2. 送信側は公開鍵を使って平文を暗号化し、受信側に送信
  3. 受信側は秘密鍵を使って暗号文を平文に復号（秘密鍵を持っている受信側しか複合できない）

この手順を、もう少し詳しく見ると以下のとおり。

  1. 受信側が、公開鍵として(p, n)、秘密鍵として(s, n)を準備し、公開鍵を公開する
  2. 送信側は、公開鍵を使って平文(plaintext)を暗号化し、暗号文(ciphertext)を生成、受信側に送信
    • T_c = T_p^p \mod n
  3. 受信側は、受け取った暗号文を秘密鍵を使って複合
    • T_p = T_c^s \mod n

公開鍵・秘密鍵の算出手順

素数の組の準備

まず、受信側で2つの素数q, rを準備する。例えばq=5, r=11とする。

素数の積nの計算

次に、q, rの積を計算し、その値をnとする。

(1)   \begin{equation*} n = qr \end{equation*}

例えばn=5 \times 11 = 55。

計算準備

q-1, r-1の最小公倍数を計算しておく。

(2)   \begin{equation*} L = LCM(p-1, q-1) \end{equation*}

例えば、L = LCM(4, 10) = 20。

公開鍵の計算

p, Lが互いに素であるようなpを選ぶ。ここで公開鍵は(p, n)となる。

(3)   \begin{equation*} p \; : \; GCM(p, L) = 1 \end{equation*}

例えば、p = 3とすると、公開鍵は(3, 55)

秘密鍵の計算

(4)   \begin{equation*} s \; : \; sp \mod L = 1 \end{equation*}

例えば、e = 7とすると、3 \times 7 \mod 20 = 1となり、秘密鍵は(7, 55)。

簡略化した暗号化の例

鍵の準備

先の公開鍵・秘密鍵の算出で例示した値を使って、暗号化の流れを見てみる。

2つの素数の組p=5, q=11を準備し、n = pq = 5 \times 11 = 55を計算した。

さらにLCM(q-1, r-1)の値から、公開鍵(p, n)、秘密鍵(s, n)を以下の様に得た。

(5)   \begin{eqnarray*} (p, n) &=& (3, 55) \\ (s, n) &=& (7, 55) \end{eqnarray*}

暗号化

平文として数列12, 26, 33を考え、送信側で公開鍵を使って、この平文を暗号化する。

(6)   \begin{eqnarray*} 12 &\rightarrow& 12^p \mod n = 12^3 \mod 55 = 1728 \mod 55 = 23\\ 26 &\rightarrow& 26^p \mod n = 26^3 \mod 55 = 17576 \mod 55 = 31 \\ 33 &\rightarrow& 33^p \mod n = 33^3 \mod 55 = 35937 \mod 55 = 22 \end{eqnarray*}

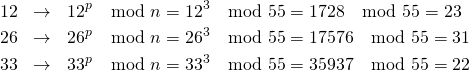
復号

受信側は受け取った暗号文を、秘密鍵を使って複合する。

(7)   \begin{eqnarray*} 23 &\rightarrow& 23^s \mod n = 23^7 \mod 55 = 3404825447 \mod 55 = 12\\ 31 &\rightarrow& 31^s \mod n = 31^7 \mod 55 = 27512614111 \mod 55 = 26\\ 22 &\rightarrow& 22^s \mod n = 22^7 \mod 55 = 2494357888 \mod 55 = 33 \end{eqnarray*}

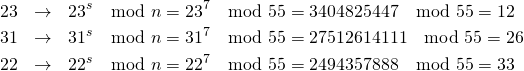
電子証明

電子証明の流れ

公開鍵と秘密鍵を使う順序を逆にすると、電子証明に仕える。その流れは以下のとおり。

  1. 発信側が公開鍵と秘密鍵を準備し、公開鍵を公開
  2. 発信側は秘密鍵を使って平文を暗号化し、受信側に送信
  3. 受信側は公開鍵を使って暗号文を平文に復号し、証明を確認（秘密鍵を持っている発信側しか公開鍵で正しい平文に復号可能な暗号文を生成できない）

簡略化した電子証明の例

暗号化の例と同じ公開鍵・秘密鍵を使って、電子証明の例を確認する。

証明書の暗号化

発信側で証明書の平文12, 26, 33を準備し、これを秘密鍵を使って暗号化。

(8)   \begin{eqnarray*} 12 &\rightarrow& 12^s \mod n = 12^7 \mod 55 = 35831808 \mod 55 = 23\\ 26 &\rightarrow& 26^s \mod n = 26^7 \mod 55 = 8031810176 \mod 55 = 16 \\ 33 &\rightarrow& 33^s \mod n = 33^7 \mod 55 = 42618442977 \mod 55 = 22 \end{eqnarray*}

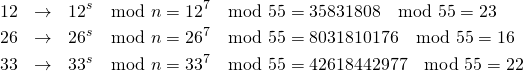
受信側は、公開鍵を使って暗号文を復号し、平文を確認（秘密鍵で暗号化した文のみ、公開鍵で適正に複合できる）。

(9)   \begin{eqnarray*} 23 &\rightarrow& 23^p \mod n = 23^3 \mod 55 = 12167 \mod 55 = 12\\ 16 &\rightarrow& 16^p \mod n = 16^3 \mod 55 = 4096 \mod 55 = 26 \\ 22 &\rightarrow& 22^p \mod n = 22^3 \mod 55 = 10648 \mod 55 = 33 \end{eqnarray*}

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です