考え方
以下のように考える。
- 文字列を文字コード化し、眺めのバッファーに先頭から収めていく
- バッファーが余った場合は、終わりまで0x00で埋める
- バッファー全体を一つの整数として、特定の値で割った余りを求める
- 余りの下位で適当なバイト数の値を取り出し、ハッシュ値とする
コード全体
上記の考え方を、クラスに実装してみる。テスト用なので、引数やオーバーフローなどのチェックはしていない。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
class Hash1(): """簡単なハッシュを生成するクラス""" def __init__(self, st): """ コンストラクター 引数 - st:ハッシュ生成対象文字列 内容 - 作業用のバッファーを準備しバッファーとハッシュ値の長さ(バイト数)を設定 - 文字列の各文字の文字コードをバッファーの背等から格納 """ self.buf = 0 self.buf_length = 16 # バッファーは16バイト self.hash_length = 8 # ハッシュ値は8バイト # 文字列中の文字のコードをバッファーに加えていく for c in st: self.buf <<= 8 self.buf += ord(c) # 文字コードを埋めた後のバッファーのバイト数 nbytes = self.get_nbytes() # バッファーの残り領域を0で埋める for n in range(0, self.buf_length - nbytes): self.buf = (self.buf << 8) + 0x00 def __str__(self): """インスタンスの文字列化メソッド""" return format(self.buf, '0x') def get_hash(self, mod_key): """ ハッシュを生成するメソッド 引数 - 剰余計算の被除数 内容 - バッファーの内容を整数とみなして剰余を計算 戻り値 - 16進表示の文字列によるハッシュ値(バイト数を調整) """ hash_value = (self.buf % mod_key) return format(hash_value, '0'+str(self.hash_length)+'X') def get_nbytes(self): """現在のバッファーのバイト数を返すメソッド""" bf = self.buf nbytes = 0 while bf != 0: nbytes += 1 bf >>= 8 return nbytes |
この実装例では、バッファーの長さを16バイト、ハッシュのバイト数は下位8バイトとし、余りを計算するための除数は実行時に引数として与えるようにしている。
実行結果
除数で変わる結果
これに適当な文字列と除数を与えてみる。
|
1 2 3 4 5 6 |
h = Hash1("My fair lady") print(h) print(h.get_hash(0xfedcba98)) # 4d792066616972206c61647900000000 # 723C2FC8 |
1文字だけ変えると、値が大きく変わり、なんとか使えそう。
|
1 2 3 4 5 6 |
h = Hash1("my fair lady") print(h) print(h.get_hash(0xfedcba98)) # 6d792066616972206c61647900000000 # 5E674DF0 |
簡単な文字列で除数を変えて試してみると、除数を「ややこしそうな値」にするとハッシュはばらつくが、除数の設定によっては入力文字列そのままの値が出たりする。
| 除数→ | 0xfedcba98 | 0xffffffff |
| A | 9ED40708 | 41000000 |
| AA | 24FECD68 | 41410000 |
| AB | B81E0A58 | 41420000 |
| AC | 4C608CB0 | 41430000 |
| BA | EB7C9820 | 42410000 |
| BB | 7FBF1A78 | 42420000 |
| BC | 14019CD0 | 42430000 |
除数の影響
被除数の値によって、なぜハッシュ値が単純になるのか。
たとえば10進数で以下の様な例を考える。
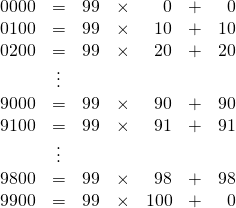
除数未満の値が余りに出ているが、上位桁のパターンがそのまま順番に現れており、先の2進数と同じ結果となっている。
そこで、より簡単な例を考えてみる。
以下の表は、左の列が被除数で、それらに対して最上段の除数で割ったときの余りを示している。被除数の1/2の桁の除数では、7あたりが最も結果がばらつき、その他の値では単純な余りの値が繰り返される。
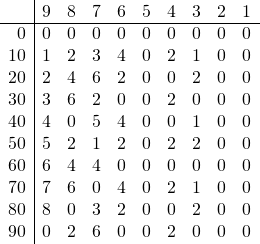
これを細分化すると、余りの値の繰り返しはより顕著であることがわかる。

先のコードは、上記の例で言えば除数を9に設定した場合に、その結果がきれいにもとの値と同じとなることに相当する。
衝突状況のチェック
除数を変化させて、アルファベット大文字1~4文字の文字列でハッシュ値の衝突が出るか確認してみた。各文字数に対するバリエーションの数は以下の通り。
- 1文字→26通り
- 2文字→26*26=676通り
- 3文字→26*26*26=17,576通り
- 4文字→26*26*26*26=456,976通り
- 合計、475,254通り
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import string ..... hash_dict = {} al = string.ascii_uppercase modkey = 0xffffffff for c1 in al: h1 = Hash1(c1).get_hash(modkey) if not(h1 in hash_dict): hash_dict[h1] = [] hash_dict[h1].append(c1) for c2 in al: s2 = c1 + c2 h2 = Hash1(s2).get_hash(modkey) if not(h2 in hash_dict): hash_dict[h2] = [] hash_dict[h2].append(s2) for c3 in al: s3 = c1 + c2 + c3 h3 = Hash1(s3).get_hash(modkey) if not(h3 in hash_dict): hash_dict[h3] = [] hash_dict[h3].append(s3) for c4 in al: s4 = c1 + c2 + c3 + c4 h4 = Hash1(s4).get_hash(modkey) if not(h4 in hash_dict): hash_dict[h4] = [] hash_dict[h4].append(s4) for itm in list(hash_dict.items()): if len(itm[1]) > 1: print('{} : {}'.format(itm[0], itm[1])) |
その結果は次の通り。
0xFEDCBA98
アルファベット1~4文字で衝突なし。
0xFEDCBA9
まだ衝突なし。
0xFEDCBA
衝突が多数発生。みな2つの文字列で衝突。たとえば
0071BB5E : [‘SZQA’, ‘ZRZW’]
003C0D52 : [‘SZQB’, ‘ZRZX’]
00065F46 : [‘SZQC’, ‘ZRZY’]
00CF8DF4 : [‘SZQD’, ‘ZRZZ’]
除数の10進値は16,702,650と文字列のバリエーションより大きいが、衝突が出始めた。
0xFFFFFFFF
意外にも衝突なし。
0xFFFFFFF
衝突が多数発生。これも2つの文字列で重複。たとえば
05A5CA5A : [‘JZZX’, ‘ZZZW’]
05A5DA5A : [‘JZZY’, ‘ZZZX’]
05A5EA5A : [‘JZZZ’, ‘ZZZY’]
除数の10進値は268,435,455とかなり大きいが、単純なパターンの値ほど衝突が起こりやすいのかもしれない。
コード詳細
コンストラクタ__init__()
- インスタンス生成時にハッシュを生成する文字列を受け取り、空のバッファーを準備
- バッファーの長さを16バイト、ハッシュ値の長さを8バイトに設定
- 引数で与えられた文字列から1文字ずつ取り出し、文字コードを追加
- バッファー長までの余った部分に0を追加
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
def __init__(self, st): """ コンストラクター 引数 - st:ハッシュ生成対象文字列 内容 - 作業用のバッファーを準備しバッファーとハッシュ値の長さ(バイト数)を設定 - 文字列の各文字の文字コードをバッファーの背等から格納 """ self.buf = 0 self.buf_length = 16 # バッファーは16バイト self.hash_length = 8 # ハッシュ値は8バイト # 文字列中の文字のコードをバッファーに加えていく for c in st: self.buf <<= 8 self.buf += ord(c) # 文字コードを埋めた後のバッファーのバイト数 nbytes = self.get_nbytes() # バッファーの残り領域を0で埋める for n in range(0, self.buf_length - nbytes): self.buf = (self.buf << 8) + 0x00 |
内部用メソッドget_nbytes()
文字コードを追加し終わったときのバッファー長を計算する処理を独立させたメソッド。
|
1 2 3 4 5 6 7 8 |
def get_nbytes(self): """現在のバッファーのバイト数を返すメソッド""" bf = self.buf nbytes = 0 while bf != 0: nbytes += 1 bf >>= 8 return nbytes |
ハッシュ値計算get_hash()
- バッファーの内容を整数として、引数で与えられた除数から剰余を計算する
- 計算結果の下位バイトを取り出して、ハッシュ値として返す
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def get_hash(self, mod_key): """ ハッシュを生成するメソッド 引数 - 剰余計算の被除数 内容 - バッファーの内容を整数とみなして剰余を計算 戻り値 - 16進表示の文字列によるハッシュ値(バイト数を調整) """ hash_value = (self.buf % mod_key) return format(hash_value, '0'+str(self.hash_length)+'X') |
文字列化メソッド__str()__
インスタンスの文字列化メソッド。
|
1 2 3 |
def __str__(self): """インスタンスの文字列化メソッド""" return format(self.buf, '0x') |