折れ線と曲線の近似誤差

円弧の長さと弦の長さの差

半径r、内角θの円弧の長さL_aは

(1) $\begin{equation*} L_a = r \theta \end{equation*}$

これに対する弦の長さは

(2) $\begin{align*} L_c &= \sqrt {r^2 + r^2 - 2 r^2 \cos \theta} \\ &= r \sqrt {2 (1 - cos \theta)} \end{align*}$

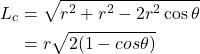
ここでL_cとL_aの比を計算すると、rを含まないθのみの関数となる。

(3) $\begin{equation*} \frac{L_c}{L_a} = \frac{\sqrt {2 ( 1 - \cos \theta ) }}{\theta} \end{equation*}$

θを度単位としてこの比をグラフにすると以下のようになる。

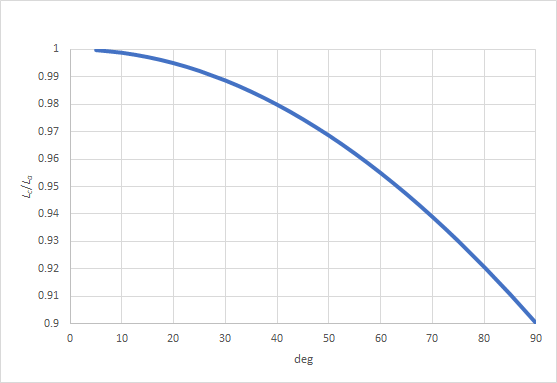
角度変化が30度弱で誤差が2%程度、20度で0.5%程度、10度になるとかなり誤差は小さくなっている。

そこでこの付近の誤差を計算してみる。

道路ネットワークのリンクを折れ線で近似する場合の誤差を考える。

式((3)の誤差率の計算結果から、円弧の内角が20～30度程度以内であれば、弧と弦の長さの差はかなり小さくなりそうだと予想される。

そこで角度に対して曲線半径rを掛けて曲線部の道路の長さを計算し、さらに誤差から曲線の道路の長さと直線で近似した長さの差を計算してみる。

ネットワークデータの用途により、許容される誤差が決まり、必要な補完点の密度が変わってくる。

たとえばメートル単位の経路案内であれば10cmオーダーの誤差は許容され、交差点での停止になると数cmなど。後者の様にミクロなコントロールや自動運転に直接データを活用する場合は、数cm程度以下の精度が必要となると想定される。