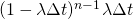# Boidの個体を実現するクラス
# Boids3.0で、Creatureクラスを継承するように変更
# 敵を回避するためのプロパティやメソッドを追加
class BoidCreature extends Creature
# private staticなクラス・プロパティ
@vMax: 0
@vMin: 0
# 描画の基本となるサイズと色
@drawSize: 8
@color: "#000000"
# 視野の深さと分離行動の回避角
@separationFieldDepth: 100
@separationAngle: 0
# 結合行動の変化角
@cohesionAngle: 0
# 整列高度の視野の長さと変化角
@alignmentFieldDepth: 100
@alignmentAngle: 0
# 敵を回避する視野の深さと変化角
@antiEnemyFieldDepth: 100
@antiEnemyAngle: 0
# 自分が属する群と敵の群への参照を保持する
constructor: (boidCluster, enemyCluster, field) ->
super(field)
@boidCluster = boidCluster
@enemyCluster = enemyCluster
@nearestCreature = null
# 個体を描画するメソッド
# canvasのコンテキストを引数で受け取る
draw: (ctx) ->
v = @v.abs()
sx = BoidCreature.drawSize * @v.x / v
sy = BoidCreature.drawSize * @v.y / v
p = 0.25
ctx.fillStyle = BoidCreature.color
ctx.beginPath()
ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy)
ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p)
ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p)
ctx.closePath()
ctx.fill()
return
# 個体を動かすメソッド
# 親クラスのメソッドをオーバーライド
# 親クラスClusterのmove()メソッドから呼ばれる
# intervalInSecは秒単位のアニメーション・フレームのインターバル
specificBehavior: (intervalInSec) ->
# 分離行動(separation)
@separation()
# 結合行動(cohesion)
@cohesion()
# 整列行動(alignment)
@alignment()
# 敵回避
@avoidEnemy()
return
# 分離行動(separation)
# 前方視角180度内で一定距離内の視野の中で、最も近い個体を避けるよう方向を変える
# 相手方の速度の向きには関係なく、相手側と反対方向に速度の向きをを少し変更する。
separation: ->
# 回避行動の方向転換計算用cos/sin
cs = Math.cos(BoidCreature.separationAngle)
sn = Math.sin(BoidCreature.separationAngle)
# 自身に最も近いBoidとEnemyの個体
@nearestCreature = null
@nearestEnemy = null
# 自分以外の群のすべての個体についてサーチ
for other in @boidCluster.creatures
if other != this
# その個体が自分の前方にいるなら
if other.isInFrontOf(this)
d = Vector.distance(this.pos, other.pos)
# その個体が視野の中にいるなら
if d <= BoidCreature.separationFieldDepth
# 既に個体がセットされていて、今回の個体の方が近ければ入れ替え
# 最初に認識した個体ならそのままセット
if @nearestCreature?
if d <= Vector.distance(@nearestCreature.pos, this.pos)
@nearestCreature = other
else
@nearestCreature = other
# 近くの個体が視野内に存在するなら回避計算
if @nearestCreature?
# 相手が自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更
if @nearestCreature.isOnTheRightOf(this)
vx = @v.x * cs - @v.y * sn
vy = @v.x * sn + @v.y * cs
else
vx = @v.x * cs + @v.y * sn
vy = -@v.x * sn + @v.y * cs
@v.x = vx
@v.y = vy
# 結合行動(cohesion)
# 前方視角180度以内の全個体の重心に向かって少し方向を変える
cohesion: ->
# 群のうち認識した個体の数とそのグループの重心
n = 0
clusterCenter = null
# 結合行動の方向転換計算用cos/sin
cs = Math.cos(BoidCreature.cohesionAngle)
sn = Math.sin(BoidCreature.cohesionAngle)
# 自分以外の群のすべての個体についてサーチ
for other in @boidCluster.creatures
if other != this
# 相手が自身の前方にいるなら、その位置を考慮
if other.isInFrontOf(this)
n++
if clusterCenter?
clusterCenter.plusEq(other.pos)
else
clusterCenter = new Vector(other.pos.x, other.pos.y)
# 前方の相手が1つでも存在すれば、結合行動をとる
if clusterCenter?
clusterCenter.divEq(n)
# 重心が自分の右にあれば左に、自分の左にあれば右に進路を変更
if clusterCenter.isOnTheRightOf(this)
vx = @v.x * cs + @v.y * sn
vy = -@v.x * sn + @v.y * cs
else
vx = @v.x * cs - @v.y * sn
vy = @v.x * sn + @v.y * cs
@v.x = vx
@v.y = vy
# 整列行動(alignment)
# 分離行動と同じ視野内の個体群の平均速度に合わせるよう少し方向を変える
alignment: ->
vMean = null
n = 0
# 整列行動の方向転換計算用cos/sin
cs = Math.cos(BoidCreature.alignmentAngle)
sn = Math.sin(BoidCreature.alignmentAngle)
# 自分以外の群のすべての個体についてサーチ
for other in @boidCluster.creatures
if other != this
# その個体が自分の前方にいるなら
if other.isInFrontOf(this)
d = Vector.distance(this.pos, other.pos)
# その個体が視野の中にいるなら
if d <= BoidCreature.alignmentFieldDepth
# 既に個体が視野内にあれば平均速度の計算を続行
n++
if vMean?
vMean.plusEq(other.v)
else
vMean = new Vector(0, 0)
# 視野内に個体がいるなら速度変更の計算へ
if vMean?
vMean.divEq(n)
if vMean.isHeadingToRightOf(@v)
vx = @v.x * cs + @v.y * sn
vy = -@v.x * sn + @v.y * cs
else
vx = @v.x * cs - @v.y * sn
vy = @v.x * sn + @v.y * cs
@v.x = vx
@v.y = vy
# Boids3.1で追加
# 敵を回避する行動で、分離行動と同じロジック
avoidEnemy: ->
# 回避行動の方向転換計算用cos/sin
cs = Math.cos(BoidCreature.antiEnemyAngle)
sn = Math.sin(BoidCreature.antiEnemyAngle)
# 自身に最も近いEnemyの個体
@nearestCreature = null
# Enemyのすべての個体についてサーチ
for enemy in @enemyCluster.creatures
# その個体が自分の前方にいるなら
if enemy.isInFrontOf(this)
d = Vector.distance(this.pos, enemy.pos)
# その個体が視野の中にいるなら
if d <= BoidCreature.antiEnemyFieldDepth
# 既に個体がセットされていて、今回の個体の方が近ければ入れ替え
# 最初に認識した個体ならそのままセット
if @nearestEnemy?
if d <= Vector.distance(@nearestEnemy.pos, this.pos)
@nearestEnemy = enemy
else
@nearestEnemy = enemy
# 近くの個体が視野内に存在するなら回避計算
if @nearestEnemy?
# Enemyが自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更
if @nearestEnemy.isOnTheRightOf(this)
vx = @v.x * cs - @v.y * sn
vy = @v.x * sn + @v.y * cs
else
vx = @v.x * cs + @v.y * sn
vy = -@v.x * sn + @v.y * cs
@v.x = vx
@v.y = vy
![]() としたとき、時刻
としたとき、時刻![]() を確率変数とした確率密度関数と確率分布関数は以下の形になる。
を確率変数とした確率密度関数と確率分布関数は以下の形になる。![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} E(t) &=& \int_0^\infty t \lambda e^{- \lambda t} dt = \int_0^\infty x e^{-x} d \frac{x}{\lambda} \\ &=& \frac{1}{\lambda} \left( \int_0^\infty e^{-x} dx - \left[ x e^{-x} \right]_0^\infty \right) = \frac{1}{\lambda} \left[ - e^{-x} - x e^{-x} \right]_0^\infty \\ &=& \frac{1}{\lambda} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-4307189de1e2d97b96b989179d8376e9_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} V(t) &=& \int_0^\infty t^2 \lambda e^{-\lambda t} dt - \left( \frac{1}{\lambda} \right)^2 = \frac{1}{\lambda^2} \int_0^\infty x^2 e^{-x} dx - \frac{1}{\lambda^2} \\ &=& \frac{1}{\lambda^2} \left( 2 \int_0^\infty x e^{-x} dx - \left[ x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \left( \left[ -2 e^{-x} -2x e^{-x} - x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-3a2963bdd0340194dcbe135f02e853e2_l3.png)
![]() で最大値をとる単調減少関数。
で最大値をとる単調減少関数。![]() 以下となるような確率は、
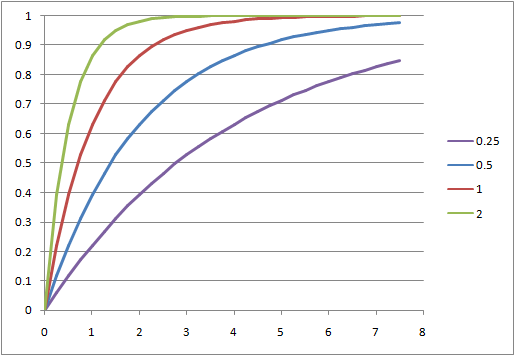
以下となるような確率は、![]() での増加率が最も大きく、その後水平に近くなっていく。
での増加率が最も大きく、その後水平に近くなっていく。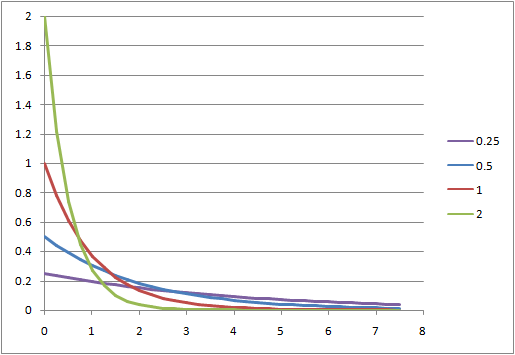
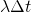 より、一定時間後に(それまで発生せず)事象が発生する確率の方が小さくなる
より、一定時間後に(それまで発生せず)事象が発生する確率の方が小さくなる