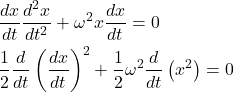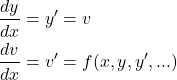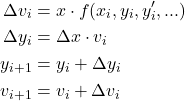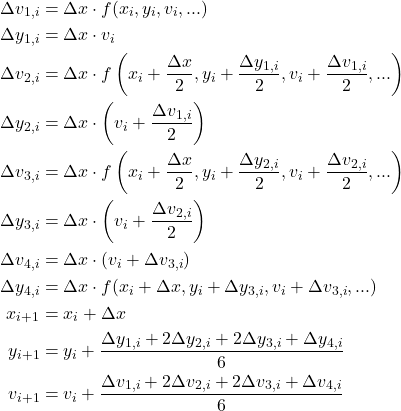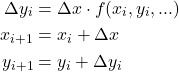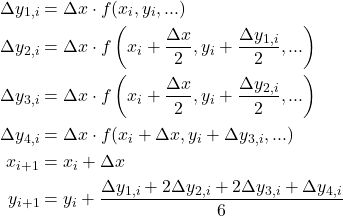概要
2階常微分方程式の数値解法、Euler法とRunge-Kutta法をPythonのモジュールとしてまとめた。
1階常微分方程式の解法についてはこちら。
基本形
以下のような方程式を考える。
(1) 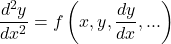
(2) 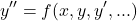
y‘(x)をv(x)と置いて以下のように変形する。
(3) 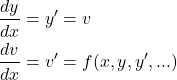
Euler法
Euler法では、iステップ目のΔv→Δyと計算し、それらを使ってi+1ステップ目のyとvを計算する。
(4) 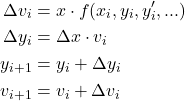
Runge-Kutta法
Runge-Kutta法も同様に、iステップ目のΔv1→Δy1を計算し、それらを使ってΔvi、Δyi (i = 1, 2, 3, 4)を計算していく。
(5) 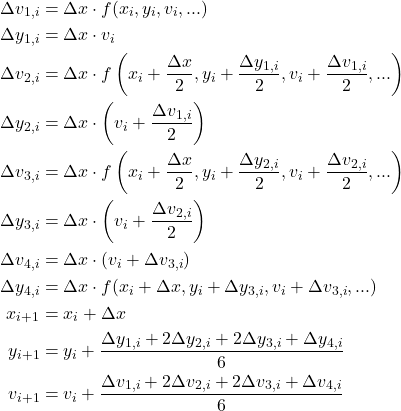
数値解法モジュール
コード
Euler法とRunge-Kutta法で2階常微分方程式を解くモジュールを、Pythonで以下の様に書いた。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# 2階常微分方程式 # - y'' = f(x, y, ...)の形の方程式が対象 # - ある計算ステップのx(i), y(i), y'(i)を与え、次のステップのy(i+1), y'(i+1)の値を返す # - 呼び出し側で、右辺f=func(x, y, v, param1, param2, ...)のように定義されている必要がある # ただしv=y' # 使用例 # - y'' = derivative(x, y, param1, param2)の場合 # - params = {'param1': 2.0, 'param2': 3.14}のようにパラメーターを定義 # - 以下のように呼び出して、ステップ計算を進める # - (y_next, v_next) = euler2(x=x_now, y=y_now, v=v_now, derivative, params)あるいは # - (y_next, v_next) = rk4_2(x=x_now, y=y_now, v=v_now, derivative, params) # funcに与える関数がパラメータを持たない場合、上の引数でparams=Noneを指定 # Euler法により2階常微分微分方程式を解く def euler2(x, y, v, dx, func, params): if params is None: dv = dx * func(x=x, y=y, v=v) dy = dx * v else: dv = dx * func(x=x, y=y, v=v, **params) dy = dx * v return (y + dy, v + dv) # 4次のRunge-Kutta法により2階常微分方程式を解く def rk4_2(x, y, v, dx, func, params): if params is None: dv1 = dx * func(x=x, y=y, v=v) dy1 = dx * v dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2) dy2 = dx * (v + dv1 / 2) dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2) dy3 = dx * (v + dv2 / 2) dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3) dy4 = dx * (v + dv3) else: dv1 = dx * func(x=x, y=y, v=v, **params) dy1 = dx * v dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2, **params) dy2 = dx * (v + dv1 / 2) dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2, **params) dy3 = dx * (v + dv2 / 2) dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3, **params) dy4 = dx * (v + dv3) return ( y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6, v + (dv1 + 2 * dv2 + 2 * dv3 + dv4) / 6 ) |
関数euler2、rk4_2の使い方はいずれも同じで、以下の通り。
x, y, vdx:計算の分割幅func:微分方程式の右辺の関数params:関数funcに与えるパラメーター
パラメーターは、呼び出し側の関数定義で設定したパラメーター名をキーとした辞書で与える。その前提で、モジュール内で**paramsとしてアンパックしている。
戻り値は実数型の数値。
使い方
モジュールの使い方の概要は以下のとおり。
- 右辺の関数を定義する
- 関数に渡すパラメーターを設定する
- 計算開始点と終了点の
xの値、分割幅dx, yとvの初期値を設定する
x, y, vの計算用リストを確保する- 計算開始点の
yとvのリストに初期値をセットする
- 計算実行
単純な放物線の微分方程式を例にしてモジュールの使い方を示す。まず、解の方程式として以下を考える。
(6) 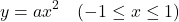
この式を2階微分した、以下の常微分方程式を解いていく。
(7) 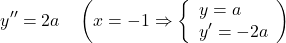
まず、必要なパッケージをインポート。diffeqは上で示したモジュールを収めている。
|
|
import numpy as np import matplotlib.pyplot as plt import diffeq |
次に、微分方程式右辺の関数を定義する(以下のderivative)。この関数はパラメーターとして係数aを1つ持っている。また、パラメーターの値を辞書で定義する。
|
|
# 微分方程式の右辺の関数 def derivative(x, y, v, a): return 2 * a # 関数に渡すパラメーター params = {'a': 1.0} |
数値計算に計算開始点x_startと終了点x_end、分割幅dx、yとvの計算初期値を設定。
|
|
# 計算に必要な値の設定 x_start = -1.0 # 計算開始点のxの値 x_end = 1.0 # 計算終了点のxの値 dx = 0.2 # 分割幅 y_initial = 1.0 # 計算開始点におけるyの初期値 v_initial = -2.0# 計算開始点におけるvの値 |
次に、予めxの計算点のリストを用意して、これに対応するy, vの値を計算・保存していく。計算点数は植木算で分割数+1とし、ループ計算に用いるリストは計算終了点を除いている。結果を保存しないなら、リストではなく逐次各ステップの計算値を次のステップの入力値にする。
また、計算開始点におけるy, vの初期値をセットしている。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 以下、計算用リストの確保 # 計算点数 num_points = int((x_end - x_start) / dx) + 1 # for分で回すためのxのリスト # n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False) # Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む) y_euler = np.linspace(x_start, x_end, num=num_points) v_euler = [0.0] * y_euler.size y_rk = [0.0] * y_euler.size v_runge_kutta = [0.0] * y_euler.size # 計算開始点に初期値をセット y_euler[0] = y_initial v_euler[0] = v_initial y_rk[0] = y_initial v_runge_kutta[0] = v_initial |
計算自体はシンプルで、定義域リストの値を1つずつ進めながら、現在の値や関数への参照、パラメーターを与えてモジュールを呼び出す。
|
|
# 計算開始 for i, x in enumerate(x_calc): # Euler法 (y_euler[i + 1], v_euler[i + 1]) = \ diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx, func=derivative, params=params) # Runge-Kutta法 (y_rk[i + 1], v_runge_kutta[i + 1]) = \ diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx, func=derivative, params=params) |
実行例
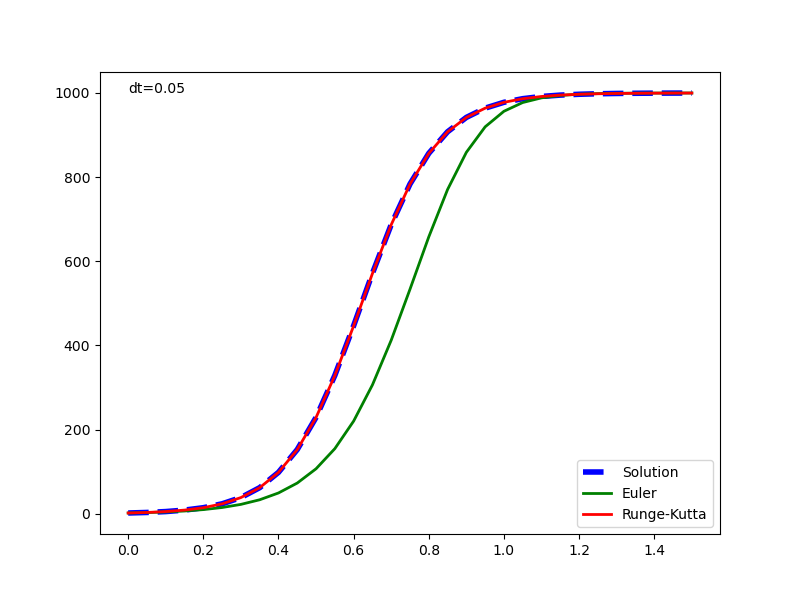
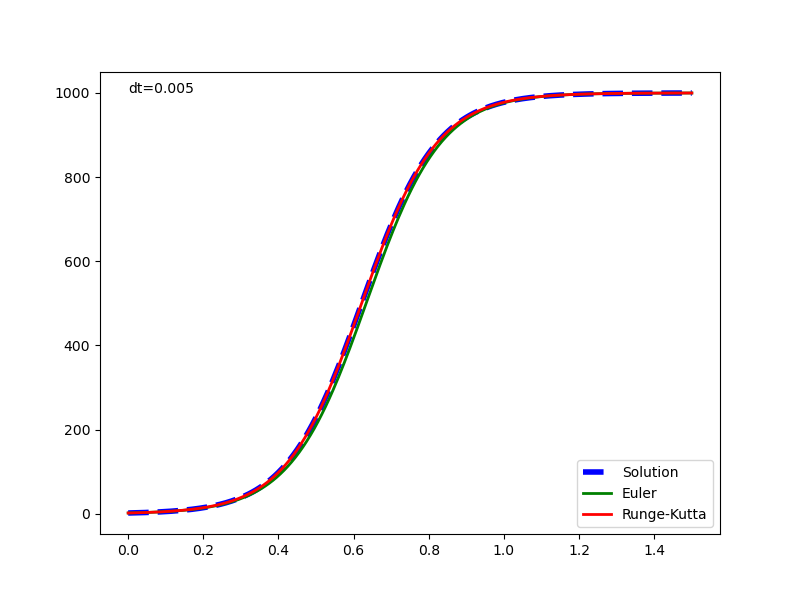
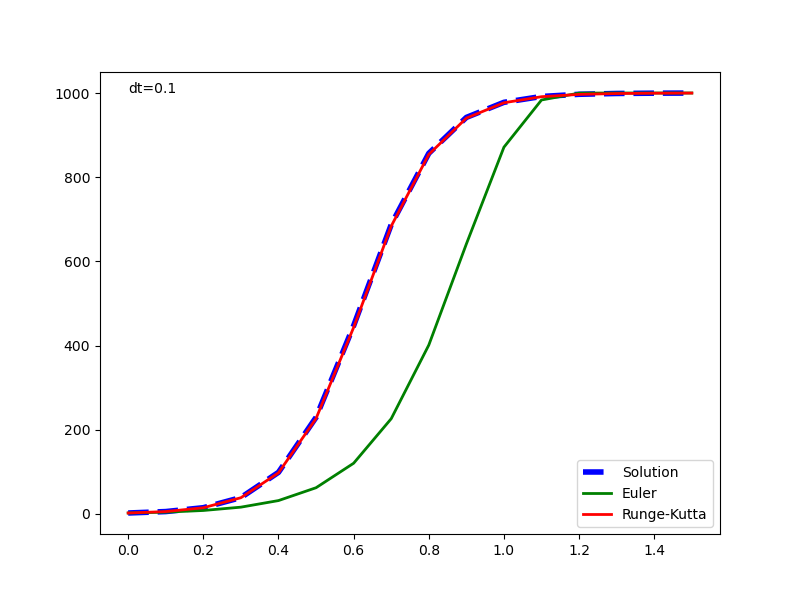
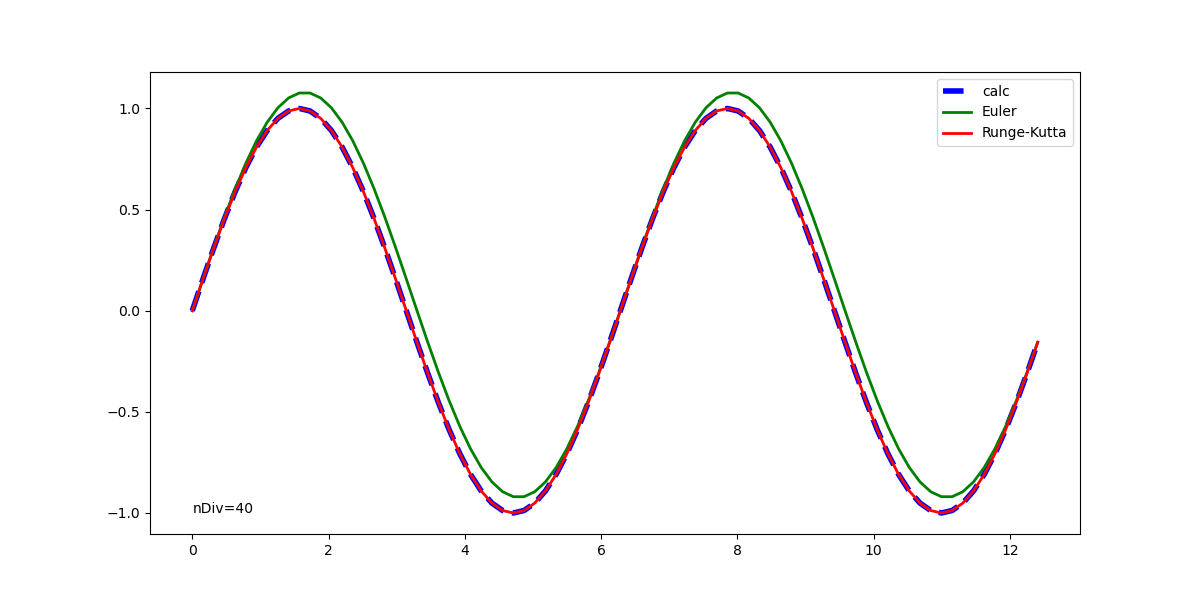
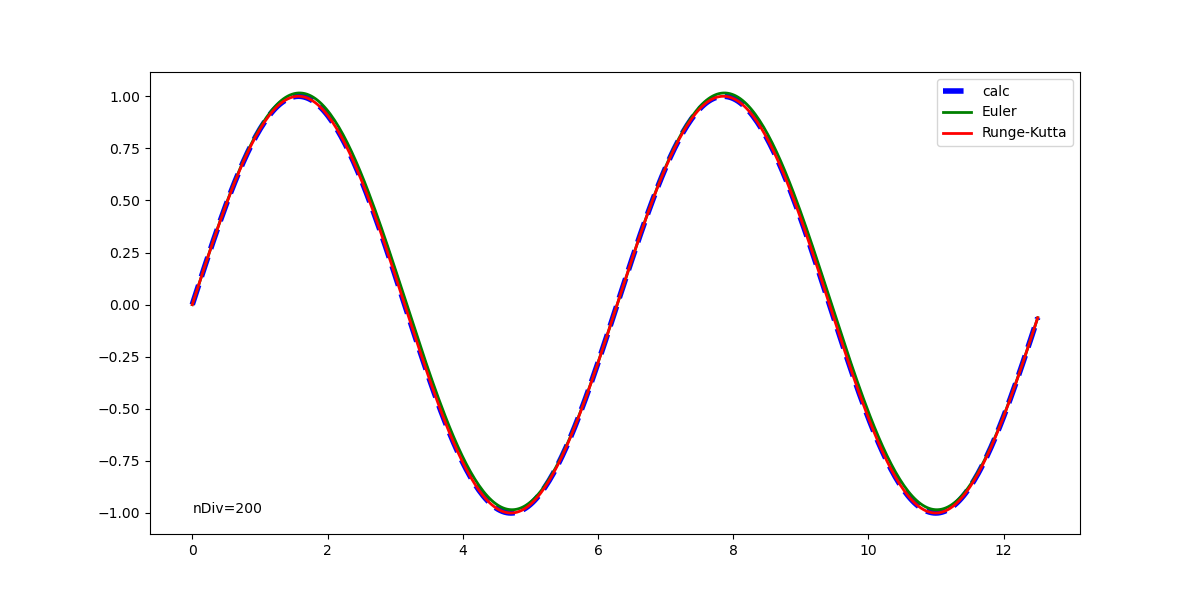
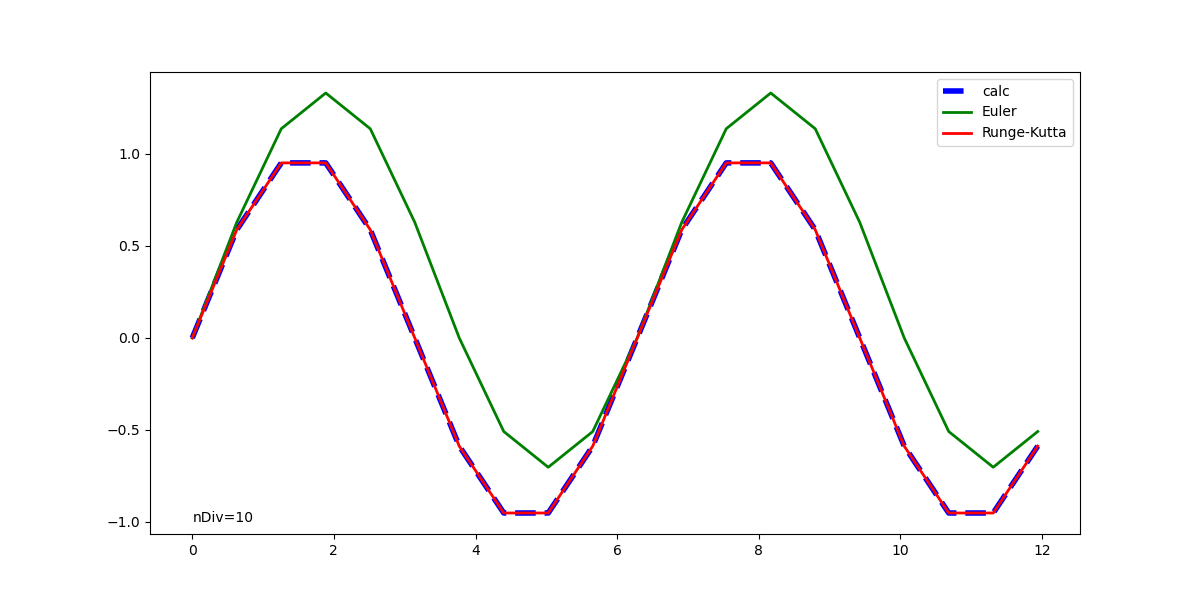
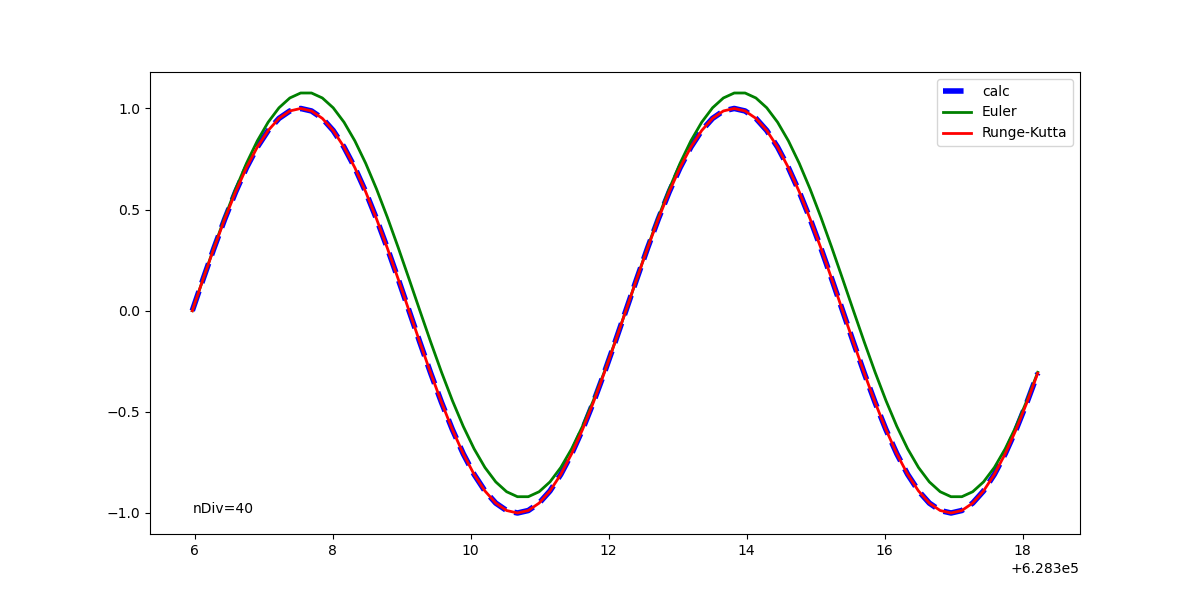
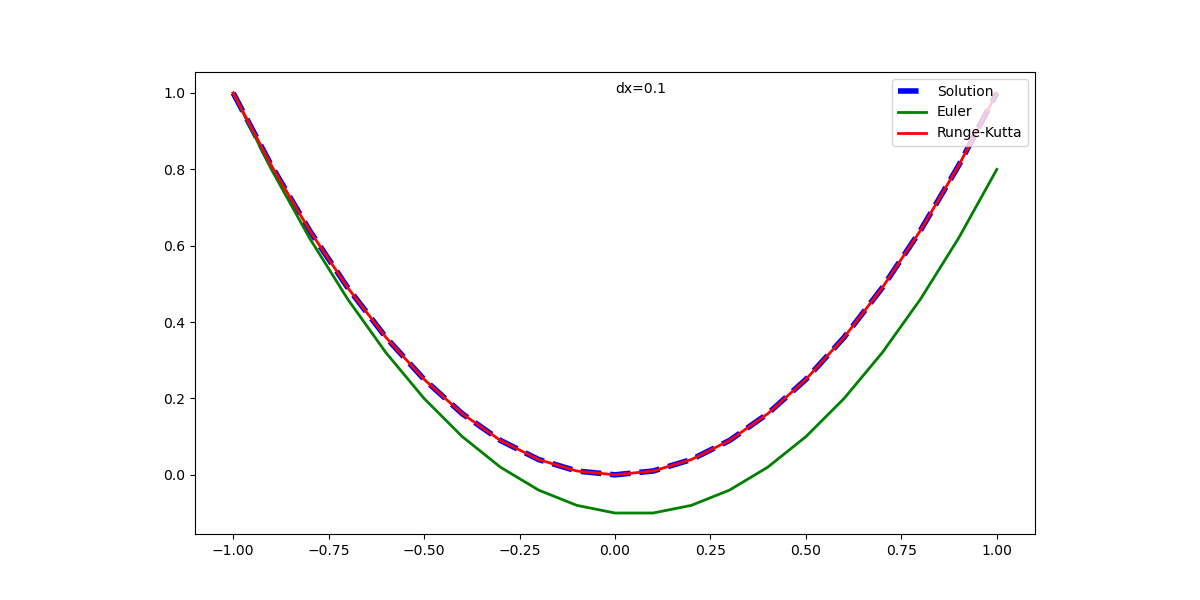
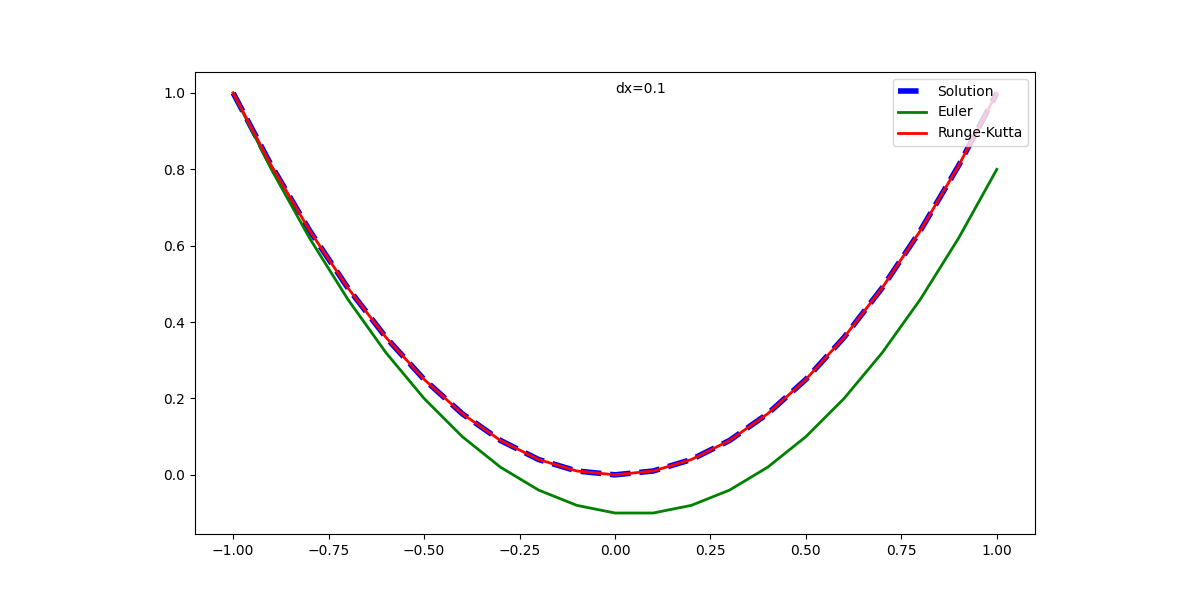
元の解析解と併せて表示した実行結果は以下の通りで、1回微分方程式の場合と同じく、Euler法の解は計算が進むごとに乖離が大きくなっている。Runge-Kutta法の解はかなり正確に解析解と一致している。
以下は、解析解も含めてグラフ表示するための、全体の実行コード。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# 放物線の1階常微分方程式 import numpy as np import matplotlib.pyplot as plt import diffeq # 解析解を計算する関数 def y_calc(x, a): return a * x**2 # 微分方程式の右辺の関数 def derivative(x, y, v, a): return 2 * a # 関数に渡すパラメーター params = {'a': 1.0} # 計算に必要な値の設定 x_start = -1.0 # 計算開始点のxの値 x_end = 1.0 # 計算終了点のxの値 dx = 0.1 # 分割幅 y_initial = 1.0 # 計算開始点におけるyの初期値 v_initial = -2.0# 計算開始点におけるvの値 # 以下、計算用リストの確保 # 計算点数 num_points = int((x_end - x_start) / dx) + 1 # for分で回すためのxのリスト # n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False) # Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む) y_euler = np.linspace(x_start, x_end, num=num_points) v_euler = [0.0] * y_euler.size y_rk = [0.0] * y_euler.size v_runge_kutta = [0.0] * y_euler.size # 計算開始点に初期値をセット y_euler[0] = y_initial v_euler[0] = v_initial y_rk[0] = y_initial v_runge_kutta[0] = v_initial # 比較用の解析解表示のための定義域と計算値 x_domain = np.linspace(x_start, x_end, num=num_points) y = y_calc(x=x_domain, a=params['a']) # 計算開始 for i, x in enumerate(x_calc): # Euler法 (y_euler[i + 1], v_euler[i + 1]) = \ diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx, func=derivative, params=params) # Runge-Kutta法 (y_rk[i + 1], v_runge_kutta[i + 1]) = \ diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx, func=derivative, params=params) # グラフ描画 fig, ax = plt.subplots(figsize=(12, 6)) ax.plot(x_domain, y, label="Solution", color="blue", linestyle="dashed", linewidth=4) ax.plot(x_domain, y_euler, label="Euler", color="green", linestyle="solid", linewidth=2) ax.plot(x_domain, y_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2) ax.set_aspect('equal') ax.text(0, 1, 'dx=' + str(dx)) ax.legend(loc="upper right") plt.show() |