概要
決定木をクラス分類に用いる場合、分類木(classification tree)とも呼ぶ。決定木は、決定境界が単調ではなく混み入っていて線形モデルでは分類が難しい場合でも対応できる。ここでは決定木のクラス分類における性質・挙動を確認する。
決定木の構築過程
2つの特徴量を持ち、2つのクラスのいずれかに属するデータについて、決定木が作られていく過程を追っていく。
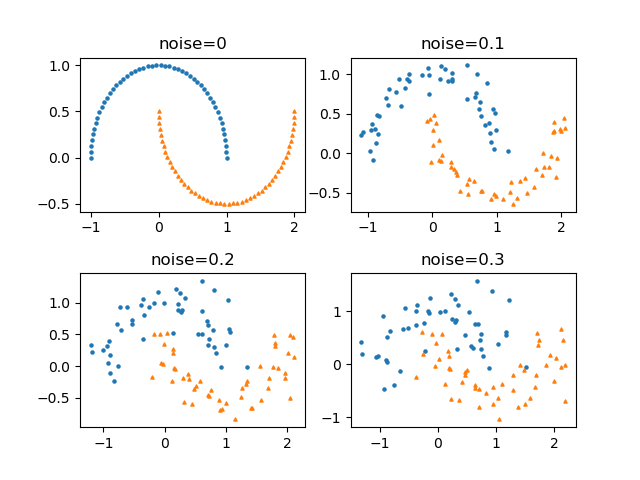
データとしては、scikit-learnのmake_moons()で得られる以下のデータを用いる。
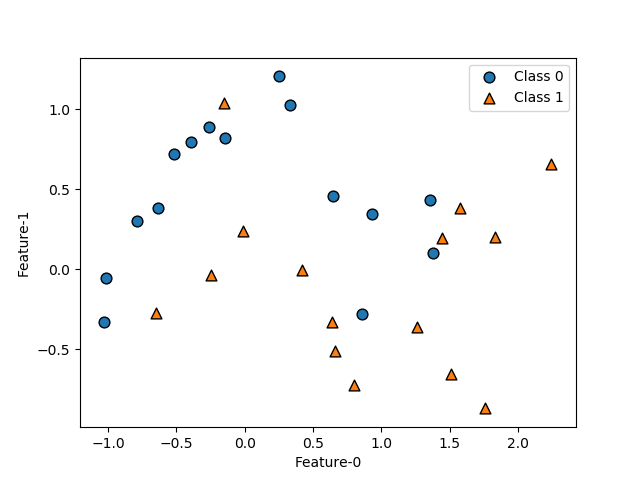
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import matplotlib.pyplot as plt from sklearn.datasets import make_moons X, y = make_moons(n_samples=30, noise=0.25, random_state=9) fig, ax = plt.subplots() ax.scatter(X[y==0][:, 0], X[y==0][:, 1], ec='k', s=60, marker='o', label="Class 0") ax.scatter(X[y==1][:, 0], X[y==1][:, 1], ec='k', s=60, marker='^', label="Class 1") ax.set_xlabel("Feature-0") ax.set_ylabel("Feature-1") ax.legend() plt.show() |
このデータセットについて、2つの特徴量のいずれかを調節して順次領域を分割していく。このとき、どのように分割するのが最も妥当かということについては、決定木の分割の考え方を参照。また、以下の実行例のコードについてはDecisionTreeClassifierに関するテストプログラムを参照。
まず最初の分割は以下の通りで、特徴量1の値0.272が境界となり、それ以下がクラス0、それより大きいとクラス1が卓越していると判定される。
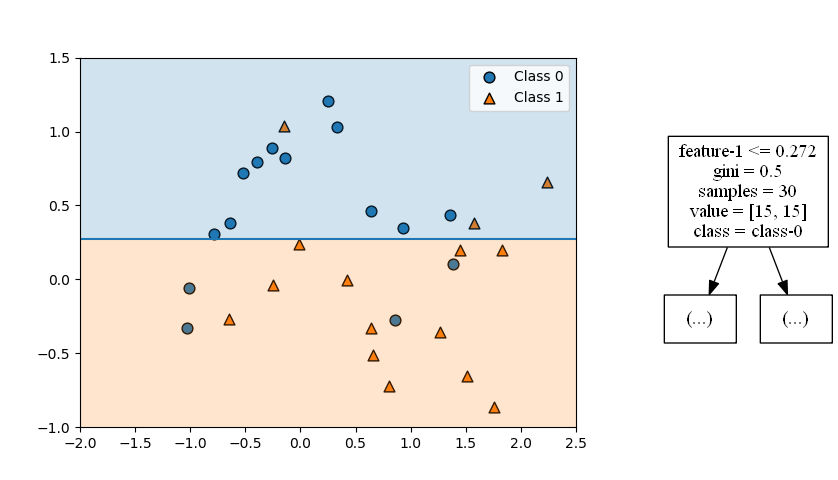
第2ステップは、第1ステップで分けられたそれぞれの領域を分割する。どちらの領域も特徴量0が境界となっていて、それぞれの領域/ノードの分布状態に応じた特性量によって左右に分けられている。
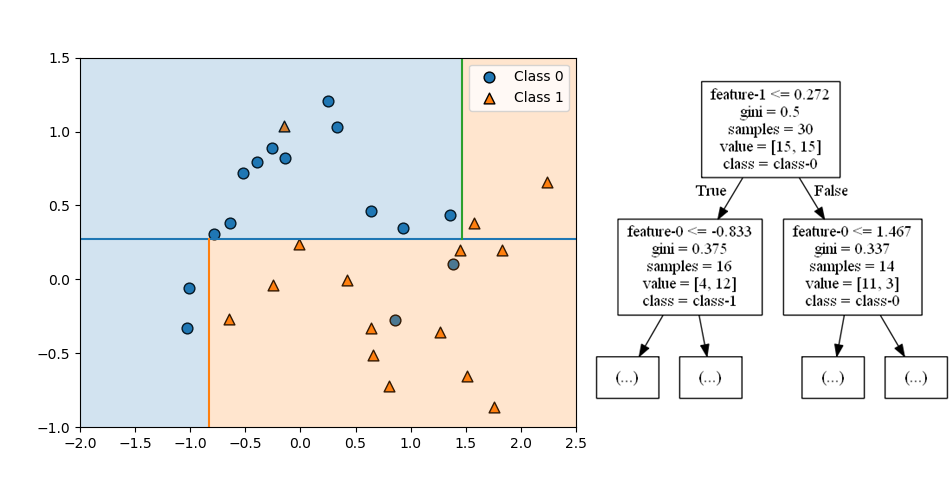
第3ステップでは、左上の領域は特徴量1で上下に、右下の領域は特徴量0で左右に分割されるが、いずれについても分割後の領域のクラスが同じになっている。利得が最も高くなるように分割しても、領域の中の擾乱クラスのデータが少ない場合はこのようになる。
なお、右上の領域はクラス1のデータが2個のみ、左下の領域クラス0のデータが2個のみと単一のクラスのデータしかないため、これ以上分割されない葉(leaf)となっている。
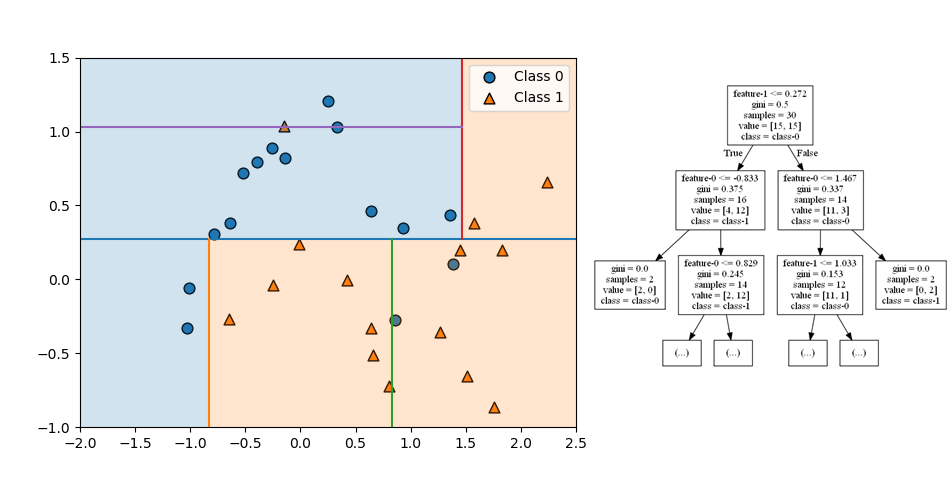
第4ステップでは、左上と右下の領域がいずれも特徴量0で左右に分割され、今度は分割後のノードが異なるクラスになっている。左上と右下の領域(ノード)がクラス1の葉となっている。
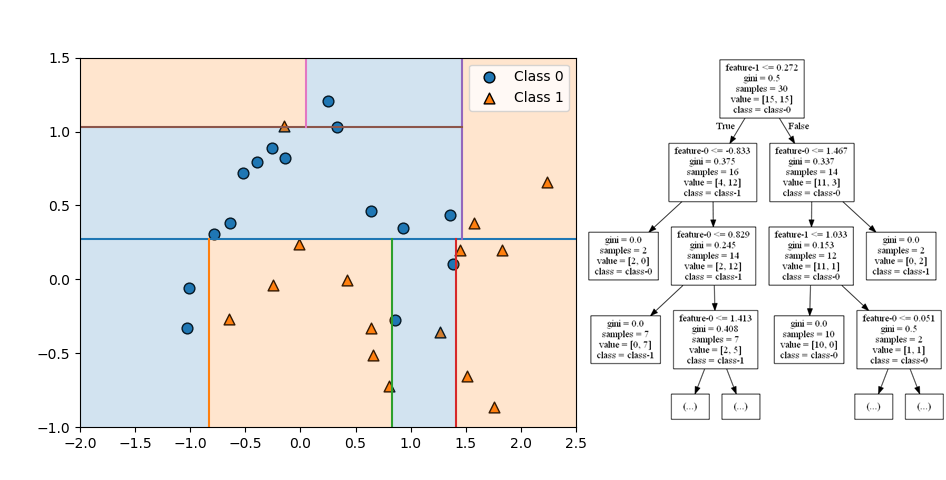
第5ステップでは下方右から2番目の領域を特徴量1で分割している。
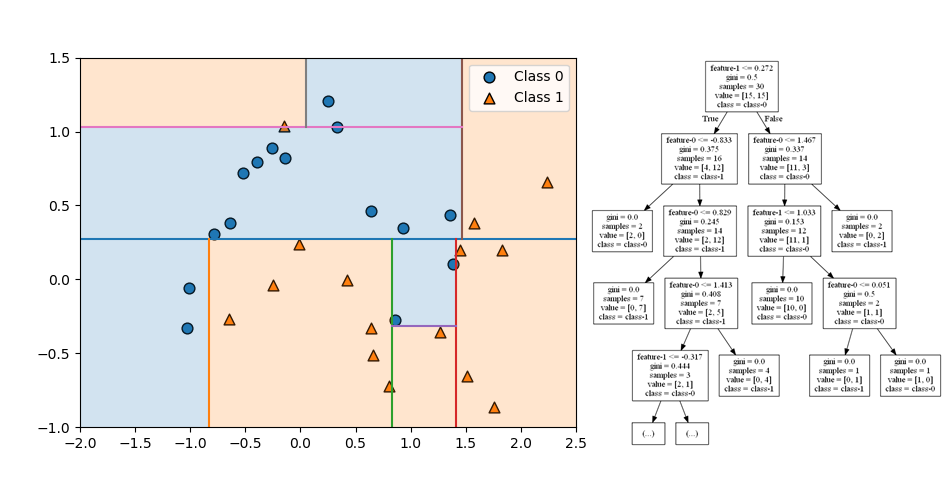
分割はここで終了。全てのノードが単一のクラスで構成された純粋な状態となっている。
全体としてはクラス0が左側の上に凸な分布、クラス1が左側の下に凸な分布と判定されていて、make_moons()が意図した分布と合っている。ただし左上に一つクラス1のデータがあるために、本来意図しない領域がクラス1と分割されている。
過学習の抑制
過学習の視覚的な例
決定木の構築過程で、1つのデータの影響で予想と異なるノード区分が発生するのが見られた。別のパターンのデータの例を以下に示す。少ないデータの影響で領域分割が複雑になっていることがわかる。
このような場合、特定のパターンの教師データに対しては適合度が高く、純粋な葉のみで構成される場合には適合度が100%になるが、他のデータに対しての適合度を下げてしまう。いわゆる過学習となってしまう。
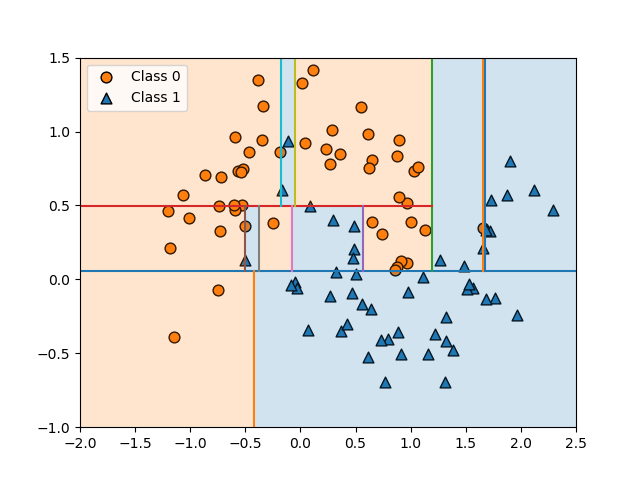
決定木の過学習を防ぐための方法として、決定木の階層をあるレベルまでに留める、いわゆる枝刈り/剪定(pruning)という考え方や、葉の切り分けを純粋なレベルより前に留める(ノード内のデータ数が2つ以上複数のデータ数になったら分割を止める)という考え方がある。
これらはscikit-learnのDecisionTreeClassifierでは、枝刈りのうち事前剪定(pre-pruning)のためのパラメーターとしてmax_depth、ノードの最小データ数のパラメーターとしてmin_samples_leafが設定できる。
max_depth~剪定
以下の例は、上記のデータに対してmax_depthを変化させたときの領域分割の様子。このパラメーターはデフォルトではNoneで可能な限り分割を行っていくが、正の整数値を指定すると、その深さまでで分割を止める。分割の深さが少なくなるにしたがってモデルが単純化されていく様子がわかる。
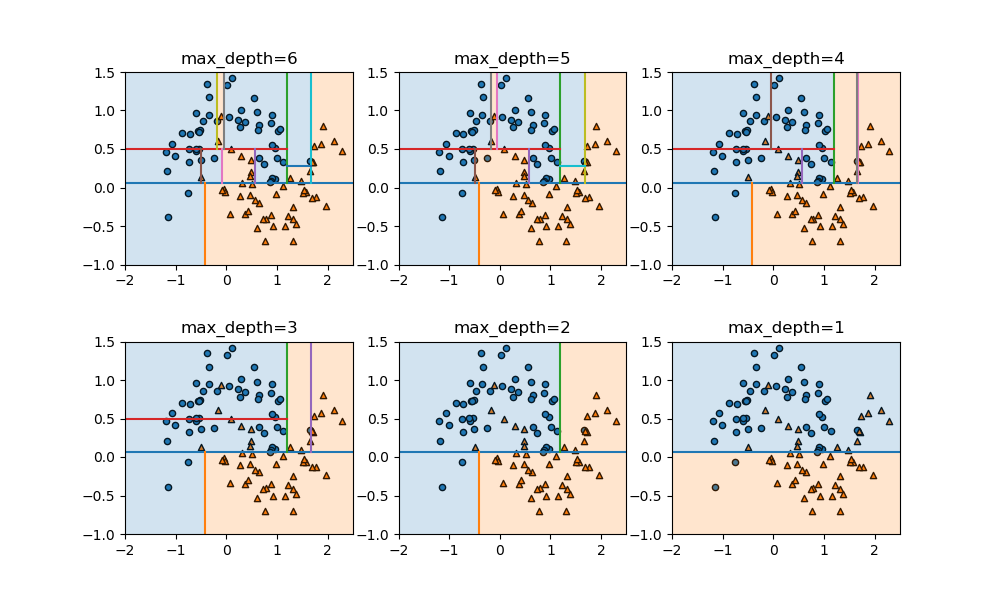
min_samples_leaf~葉の純度の制限
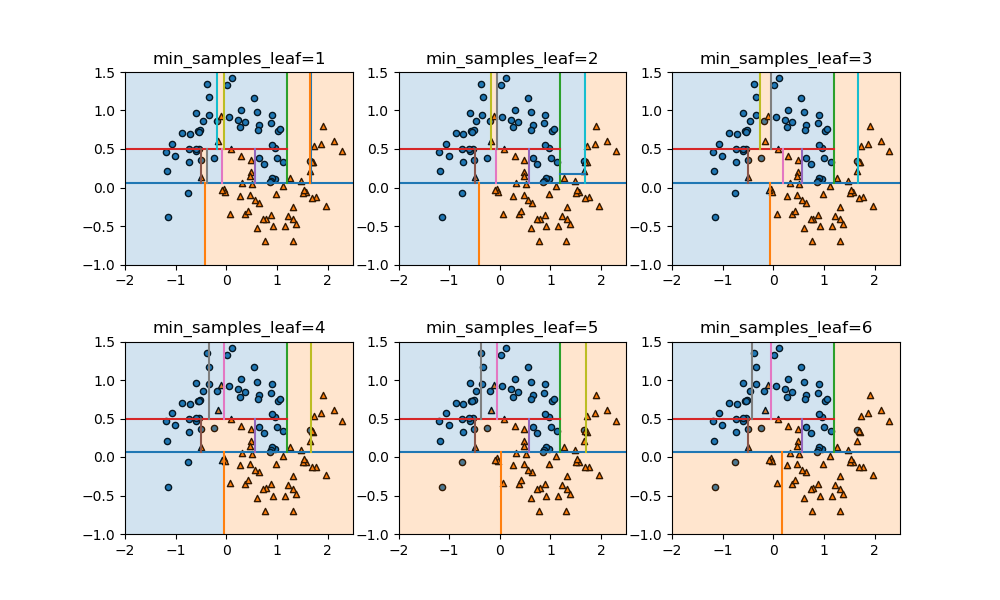
min_samples_leafはデフォルトでは1で、ノードが完全に純粋でない限りデータ数が1個になるまで分割を試みる。この値を変化させて、異なるクラスのデータを含んでいても分割を行わないようにした場合の領域分割の状況を見てみる。
枝刈りに比べてモデルの複雑さは回避しながら、それらしい領域分割になっている。これは、事前枝刈りが各ノードの不純度に関わらず同じレベルで計算を止めるのに対して、葉の純度を個別にコントロールしているために柔軟に分割が進められているためと考えられる。
cancerデータによる確認
剪定による過剰適合の抑制
breast_cancerデータセットに対してDecisionTreeClassifierを適用してクラス分類し、訓練セットとテストセットのスコアを計算する。リーフノードが純粋になるまで木を成長させた場合と、深さ4で事前剪定をした場合のスコアを比較してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import pydotplus as pdp from sklearn.model_selection import train_test_split from sklearn.datasets import load_breast_cancer from sklearn.tree import DecisionTreeClassifier, export_graphviz ds = load_breast_cancer() X_train, X_test, y_train, y_test = train_test_split(ds.data, ds.target, stratify=ds.target, random_state=42) clf = DecisionTreeClassifier(random_state=0) clf.fit(X_train, y_train) print("Tree depth: {}".format(clf.get_depth())) print("Training score:{:6.3f}".format(clf.score(X_train, y_train))) print("Test score :{:6.3f}".format(clf.score(X_test, y_test))) print() clf4 = DecisionTreeClassifier(max_depth=4, random_state=0) clf4.fit(X_train, y_train) print("Tree depth: {}".format(clf4.get_depth())) print("Training score:{:6.3f}".format(clf4.score(X_train, y_train))) print("Test score :{:6.3f}".format(clf4.score(X_test, y_test))) |
出力結果は以下の通り。完全な木は7層で、訓練セットに対しては全データに適合しており、テストセットに対しては93.7%の適合率。一方、深さ4で枝刈りをした場合は、訓練セットに対する適合率は下がるがテストセットの適合率は上がり、過剰適合が抑制されている。
|
1 2 3 4 5 6 7 |
Tree depth: 7 Training score: 1.000 Test score : 0.937 Tree depth: 4 Training score: 0.988 Test score : 0.951 |
剪定の深さに対するスコアの変化
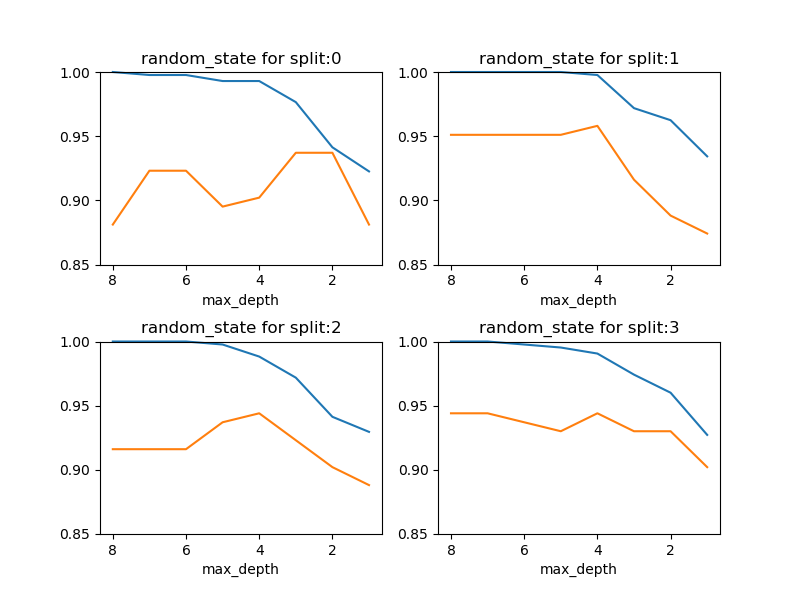
事前剪定の深さレベルを変化させたときの、訓練セットとテストセットに対するスコアの変化を確認する。train_test_split()の乱数系列によって結果のパターンが異なるが、概ねmax_depth=4で適合不足と過剰適合のバランスが最もとれているようであり、スコアは0.95程度。
ただし、そもそも決定木の深さがそれほど深くなく、max_depthのバリエーションが数個となるので、線形モデルにおけるハイパーパラメーターのような連続的な曲線は描き難い。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
max_depths = np.arange(8, 0, -1) training_scores = np.empty(max_depths.size) test_scores = np.empty(max_depths.size) fig, axs = plt.subplots(2, 2, figsize=(8, 6)) fig.subplots_adjust(hspace=0.4) ax_1d = axs.reshape(axs.size) random_state_list = [0, 1, 2, 3] for random_state, ax in zip(random_state_list, ax_1d): X_train, X_test, y_train, y_test =\ train_test_split(ds.data, ds.target, random_state=random_state) for i, max_depth in enumerate(max_depths): clf = DecisionTreeClassifier(max_depth=max_depth, random_state=0) clf.fit(X_train, y_train) training_scores[i] = clf.score(X_train, y_train) test_scores[i] = clf.score(X_test, y_test) ax.plot(max_depths, training_scores, clip_on=False) ax.plot(max_depths, test_scores) ax.set_xlim(ax.get_xlim()[::-1]) ax.set_ylim(0.85, 1) ax.set_xlabel("max_depth") ax.set_title("random_state for split:{}".format(random_state)) plt.show() |
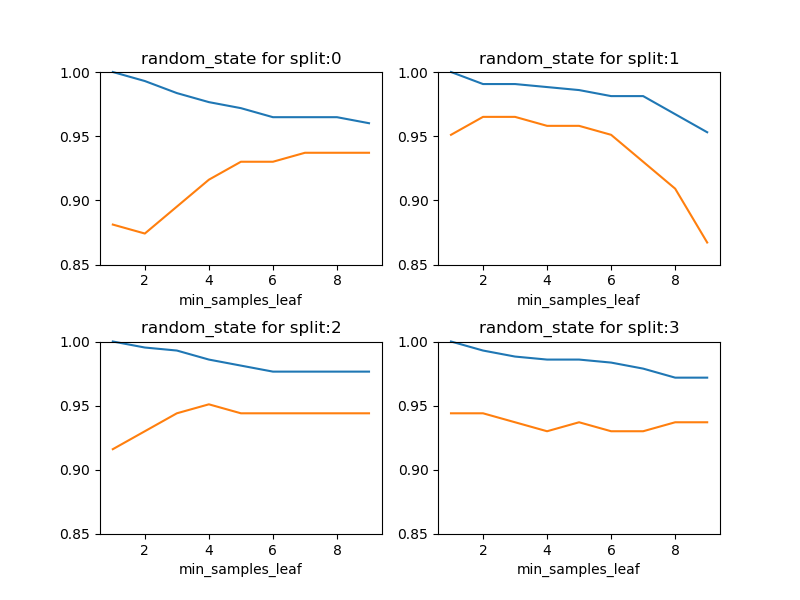
リーフの最小サンプル数に対するスコアの変化
葉ノードの最小サンプル数を一定値以上とするmin_samples_leafを変化させたときの、訓練セットとテストセットの変化を見てみたが、乱数系列によってけっこうパターンがばらついている。この傾向は、max_depthを変化させても変わらなかった。
特徴量重要度
特徴量重要度の特性
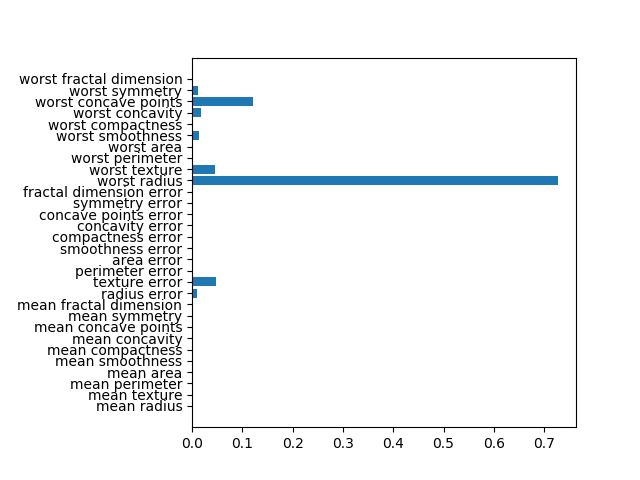
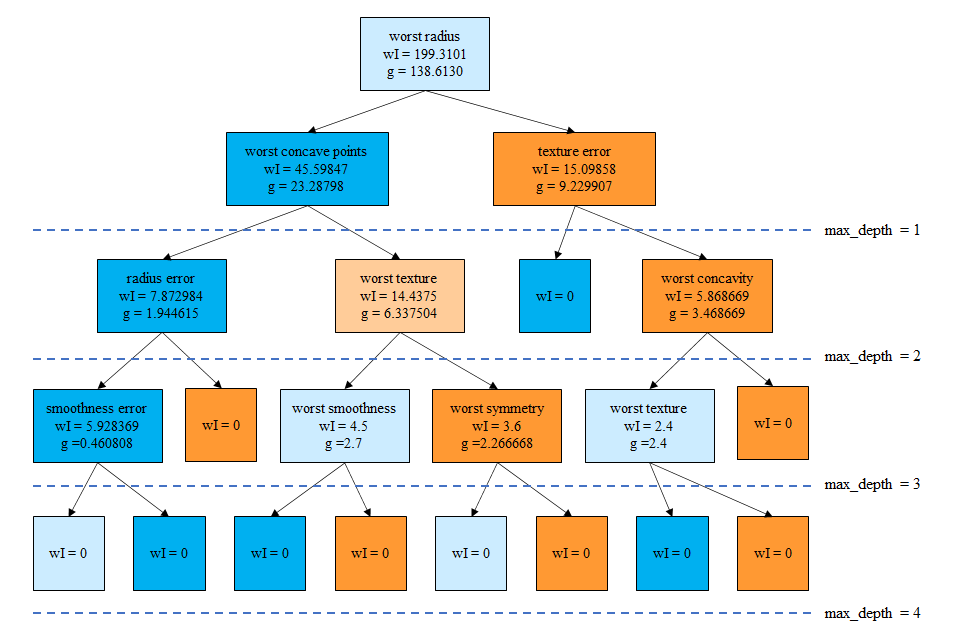
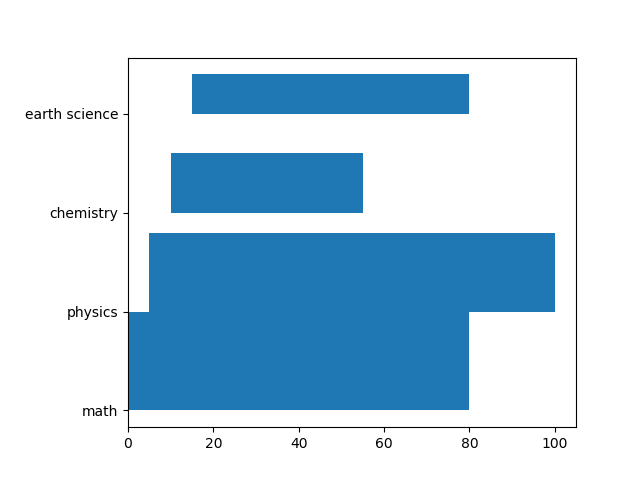
breast_cancerデータセットを深さ4で剪定した決定木によってクラス分類した場合の特徴量重要度は以下のようになる。このグラフを表示するコードや特徴量重要度の計算方法についてはこちらを参照。
|
1 2 3 4 5 6 7 8 9 10 |
feature importance 10 radius error 0.010197 11 texture error 0.048398 14 smoothness error 0.002416 20 worst radius 0.726829 21 worst texture 0.045816 24 worst smoothness 0.014158 26 worst concavity 0.018188 27 worst concave points 0.122113 28 worst symmetry 0.011885 |
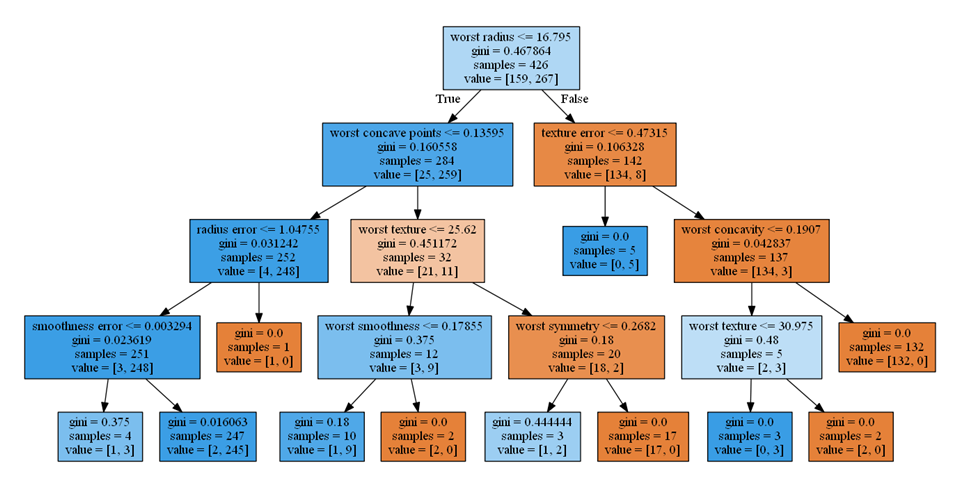
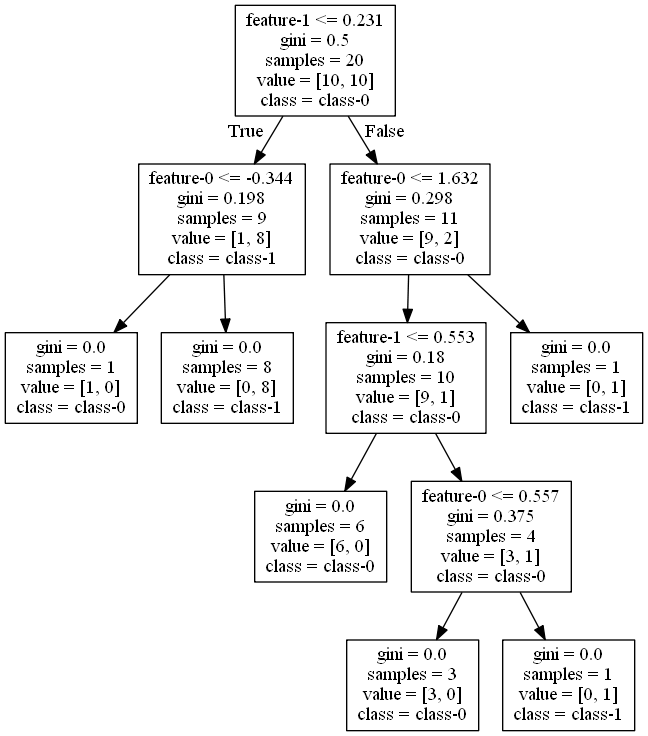
このグラフと以下の決定木を比べ、重要度が大きい順に調べてみると以下のようなことがわかる。
- worst radius(0.726)、第0層の不純度が高いノードを2つのクラスに分割し、分割後のノードの純度が高い
- worst concave points(0.122)、第1層の左側のノード、259個のクラス1のデータの大部分を左側の子ノードに切り出しつつ、クラス0のデータも25を4と21と切り分けている
- texture error(0.048)、第1層の右側のノード、クラス0のデータを完全に右の子ノードに切り分け、左の子ノードは不純度はゼロ
- worst textureは(0.045)、第2層の左から2番目のノード、データ数は少ないが、左の子ノードにクラス1のデータを9/11、右の子ノードにクラス0のデータを18/21と子ノードの純度が高い
- radius error(0.010)、第2層の左のノード、クラス1のデータを完全に左の子ノードに切り分け、右の子ノードの不純度はゼロ
特徴量重要度の計算方法や上記の特徴から、その性質は以下のように整理できる。
- 重要度は0~1の間の値をとる
- 浅いノードの対象特徴量ほど重要度が高い傾向(ただし、データの分布による可能性あり)
- 分割後の子ノードの純度が高いほど重要度が高い傾向
- 重要度の値は、どのクラスの切り分けに効いているかとは無関係
特徴量重要度の大きさは、枝を分離するときに重要な特徴量を示唆するが、その特徴量の大小とクラス分類の関係までは知ることができない。
線形モデルの特徴量係数との対比
特徴量重要度をLogistic回帰における特徴量の係数と比較してみる。以下はL2正則化によるLogistic回帰モデルをbreast_cancerデータに適用した場合の特徴量係数。
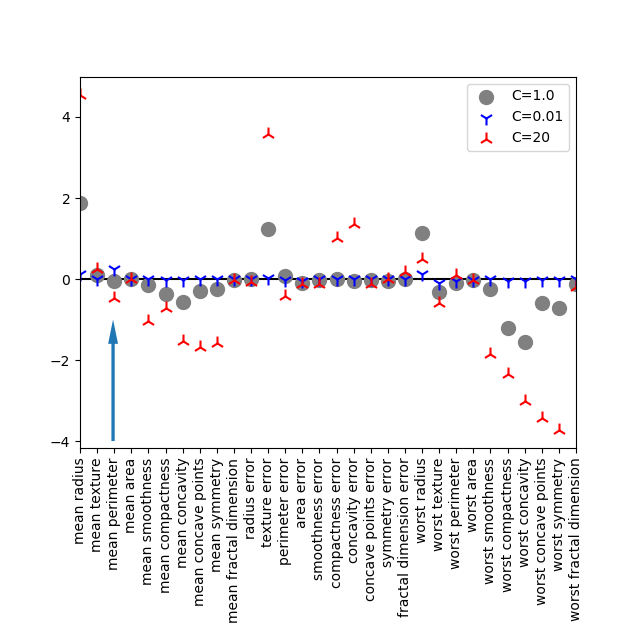
worst radiusについては、決定木での重要度が最も高いが、Logistic回帰でも比較的特徴量の重みは大きい。Logistic回帰の場合はこの特徴量がターゲット1(malignant:良性)であることを示唆しているが、決定木の場合にはそのような情報は得られない。
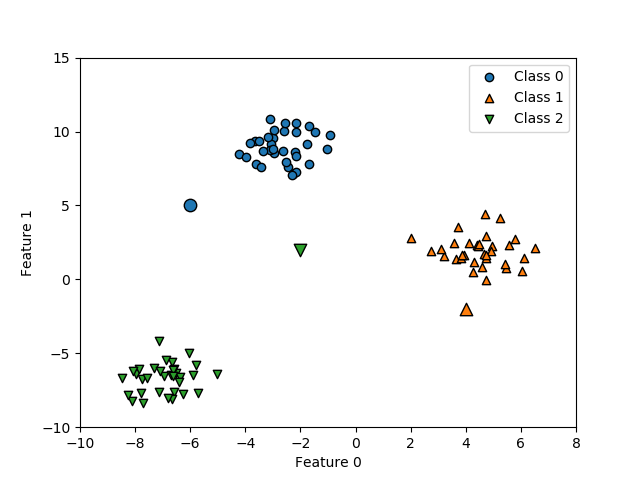
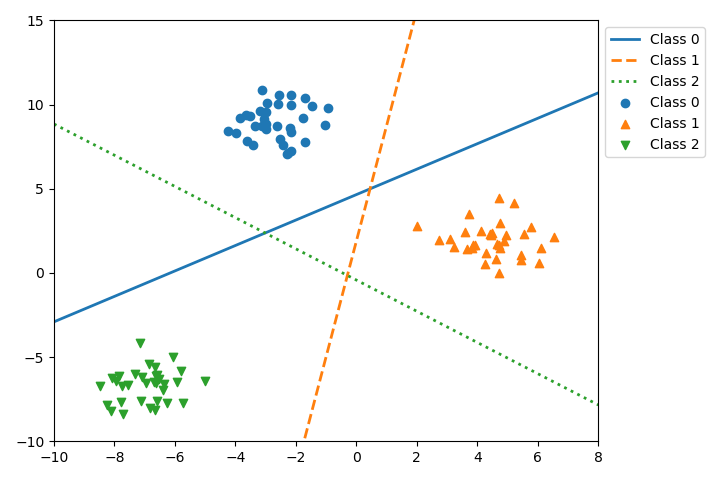
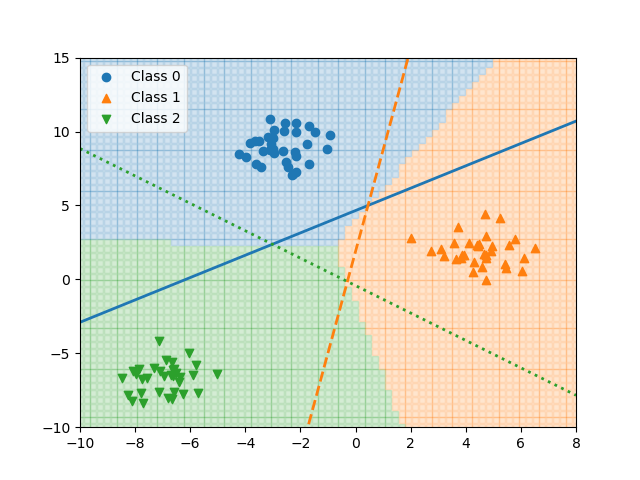
単調でないクラス分類
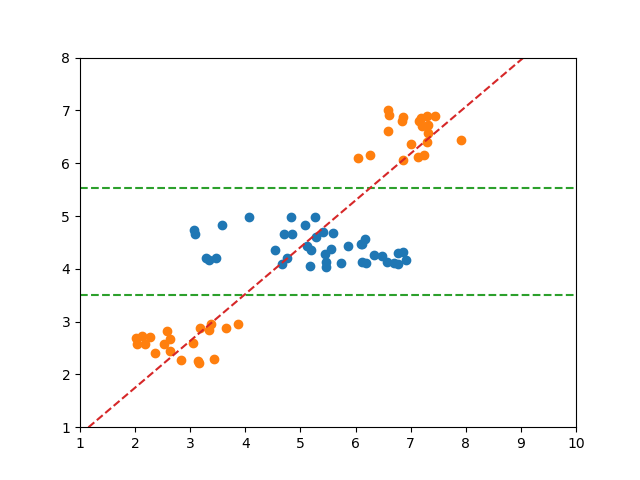
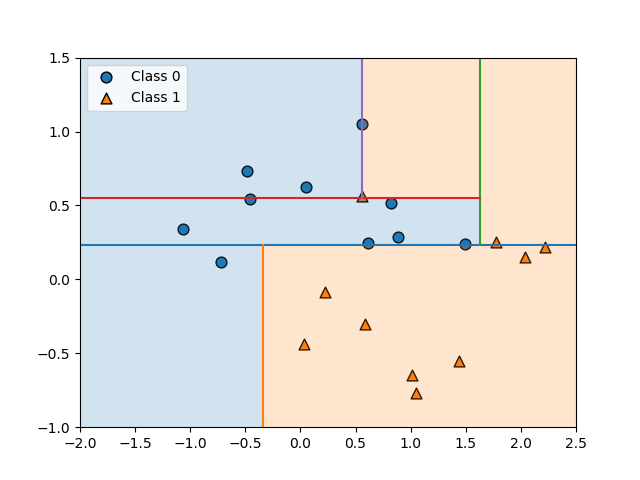
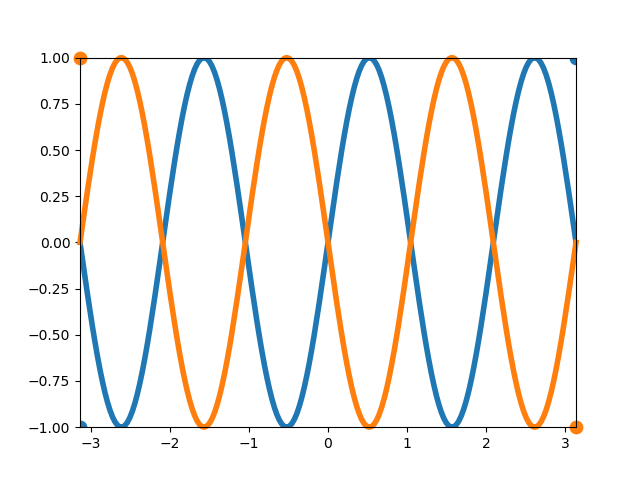
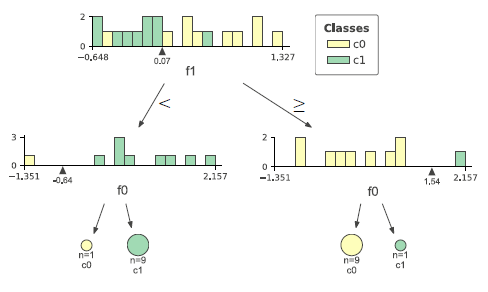
以下の例では、2つのクラス分類の境界が必ずしも1つではない。
Logistic回帰モデルの場合、一つの直線で分離しようとした結果、境界は赤い線のようになり、スコアも0.66625とかなり低い。
決定木はこのような場合でも分類可能だが、そもそもこのようなケースでは(それが決定木の性質ではなく本質的に)決定境界に対する大小だけでクラス分類を論ずることができない。
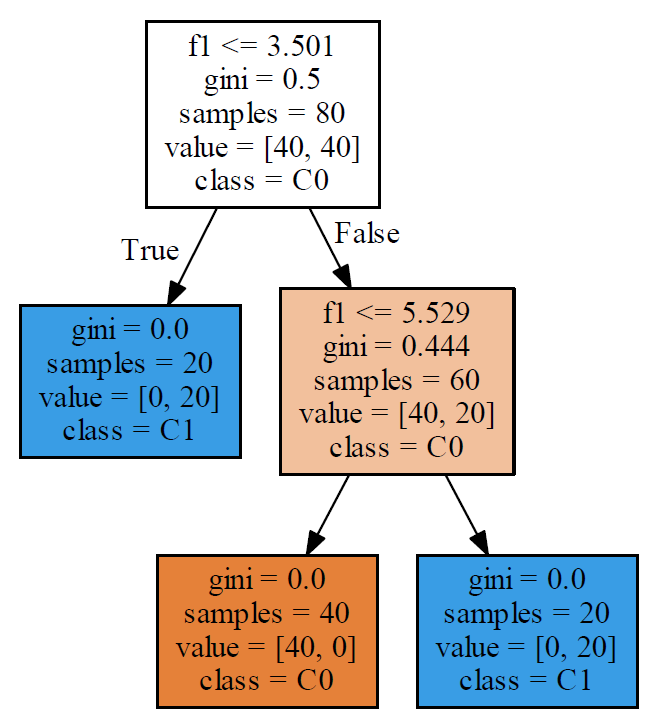
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
import numpy as np import numpy.random as rnd import matplotlib.pyplot as plt import graphviz from sklearn.tree import DecisionTreeClassifier, export_graphviz from sklearn.linear_model import LogisticRegression n0 = 40 n1a = 20 n1b = 20 rnd.seed(0) f0_0 = rnd.rand(n0) * 4 + 3 f1_0 = rnd.rand(n0) * 1 + 4 f0_1a = rnd.rand(n1a) * 2 + 2 f1_1a = rnd.rand(n1a) * 1 + 2 f0_1b = rnd.rand(n1b) * 2 + 6 f1_1b = rnd.rand(n1b) * 1 + 6 X0 = np.hstack((f0_0.reshape(-1, 1), f1_0.reshape(-1, 1))) X1a = np.hstack((f0_1a.reshape(-1, 1), f1_1a.reshape(-1, 1))) X1b = np.hstack((f0_1b.reshape(-1, 1), f1_1b.reshape(-1, 1))) X = np.vstack((X0, X1a, X1b)) y0 = np.zeros(n0) y1a = np.ones(n1a) y1b = np.ones(n1b) y = np.hstack((y0, y1a, y1b)) clf = DecisionTreeClassifier().fit(X, y) logreg = LogisticRegression().fit(X, y) print(logreg.score(X, y)) dot_data= export_graphviz(clf, out_file=None, feature_names=["f0", "f1"], class_names=["C0", "C1"], filled=True) graph = graphviz.Source(dot_data) graph.render("image", view=True) f0_min, f0_max = 1, 10 f1_min, f1_max = 1, 8 b = logreg.intercept_ w = logreg.coef_.reshape(logreg.coef_.size) border_left = (-b - w[0] * f0_min) / w[1] border_right = (-b - w[0] * f0_max) / w[1] fig, ax = plt.subplots() ax.scatter(X[y==0][:, 0], X[y==0][:, 1]) ax.scatter(X[y==1][:, 0], X[y==1][:, 1]) th1 = clf.tree_.threshold[0] th2 = clf.tree_.threshold[2] ax.plot([f0_min, f0_max], [th1, th1], c='tab:green', linestyle='dashed') ax.plot([f0_min, f0_max], [th2, th2], c='tab:green', linestyle='dashed') ax.plot([f0_min, f0_max], [border_left, border_right], c='tab:red', linestyle='dashed') ax.set_xlim(f0_min, f0_max) ax.set_ylim(f1_min, f1_max) plt.show() |
max_features~特徴量選択
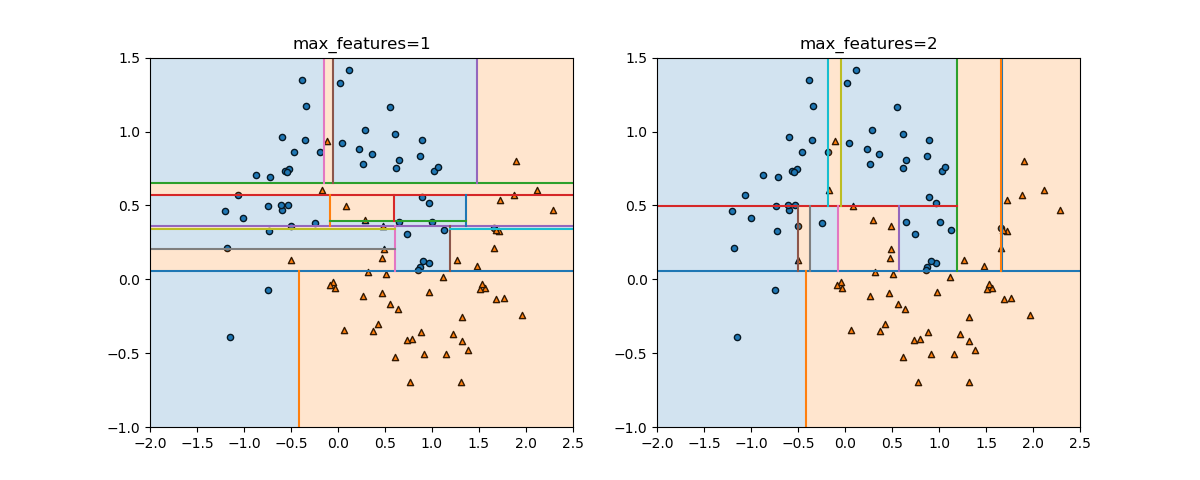
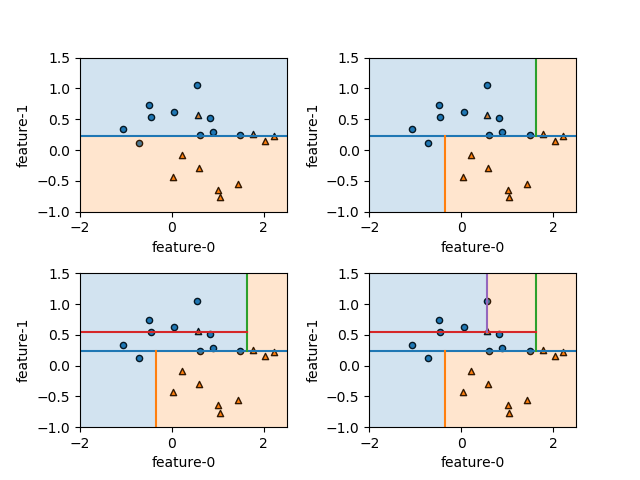
DecisionTreeClassifierのコンストラクターのパラメーターの1つ、max_featuresについて。このパラメーターがデフォルトのNoneの場合やautoを指定した場合、n_featuresすなわちすべての特徴量が比較され、最も分離の性能がいいものが選ばれる。一方、このパラメーターに整数を指定すると、分離の際にランダムにその数だけ特徴量が選ばれ、その中で分離の性能がいいものが選ばれる。max_features=1とすると、ランダムに選ばれた特徴量が、その分離性能に関わらず用いられる。
以下は、make_moonsで生成された特徴量数2のデータセットについて、max_featuresを1、2と変えた時の実行結果。max_features=1の場合は、各深さにおいて特徴量1、2がランダムに選ばれる。これは必ずしも最適な分割とならないため、ノイズのように分割が滑らかになっていない。
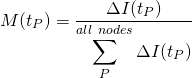
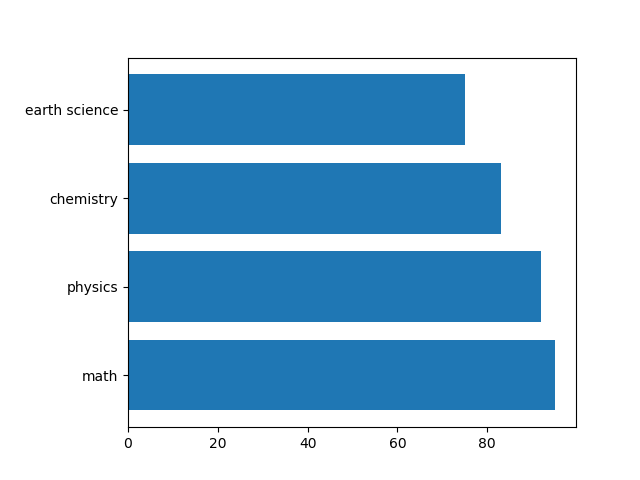
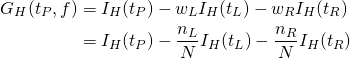
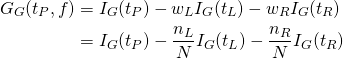
![Rendered by QuickLaTeX.com \begin{align*} w_{cf} &= \left[ \begin{array}{rrr} -0.17492222 & 0.23140089 \\ 0.4762125 & -0.06936704 \\ -0.18914556 & -0.20399715 \end{array} \right] \\ b_c &= [-1.07745632 \quad 0.13140349 \quad -0.08604899] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-8fbdc9a0c6266b87c93914dfd375a1e0_l3.png)