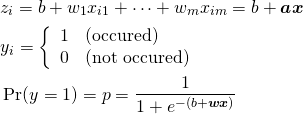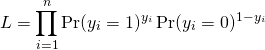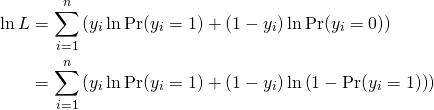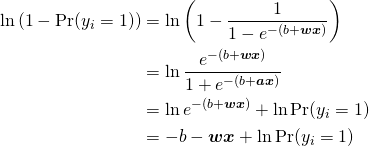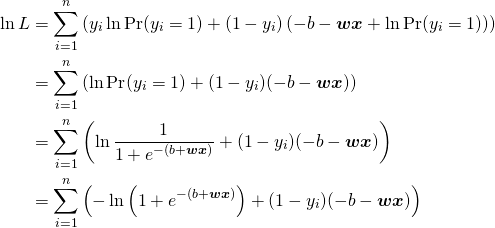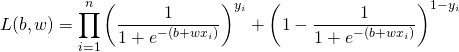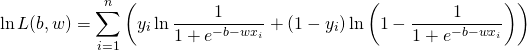概要
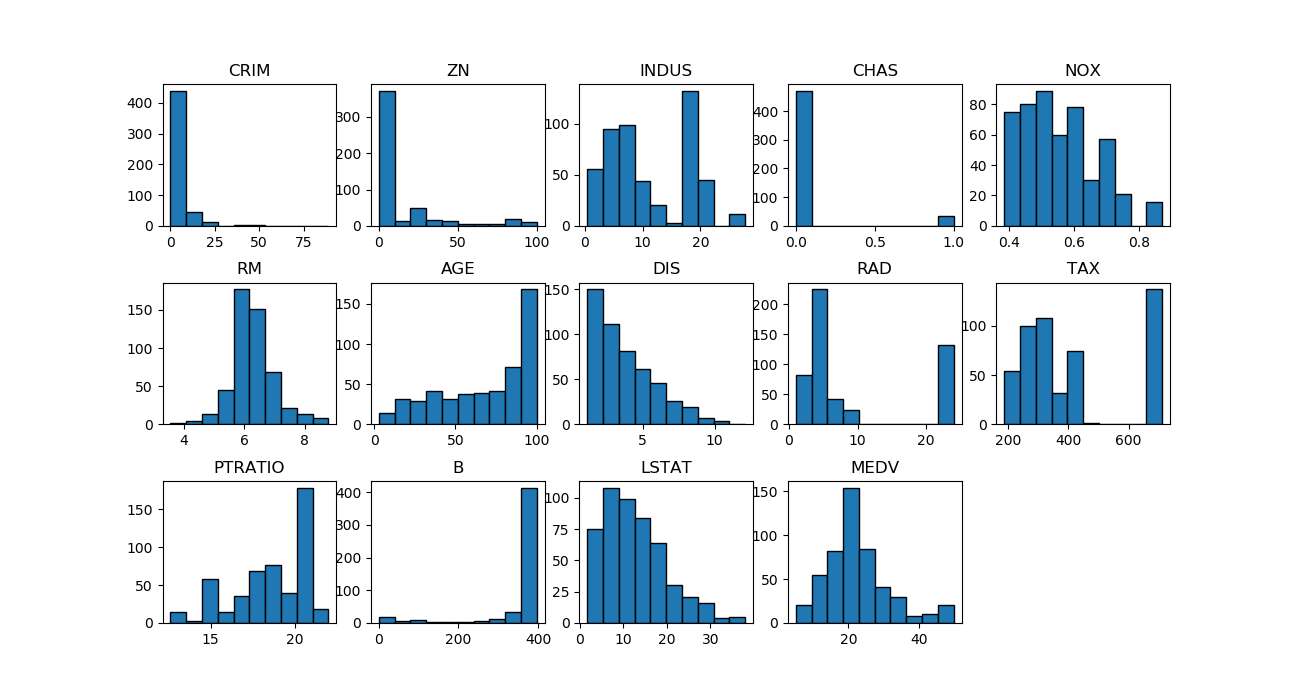
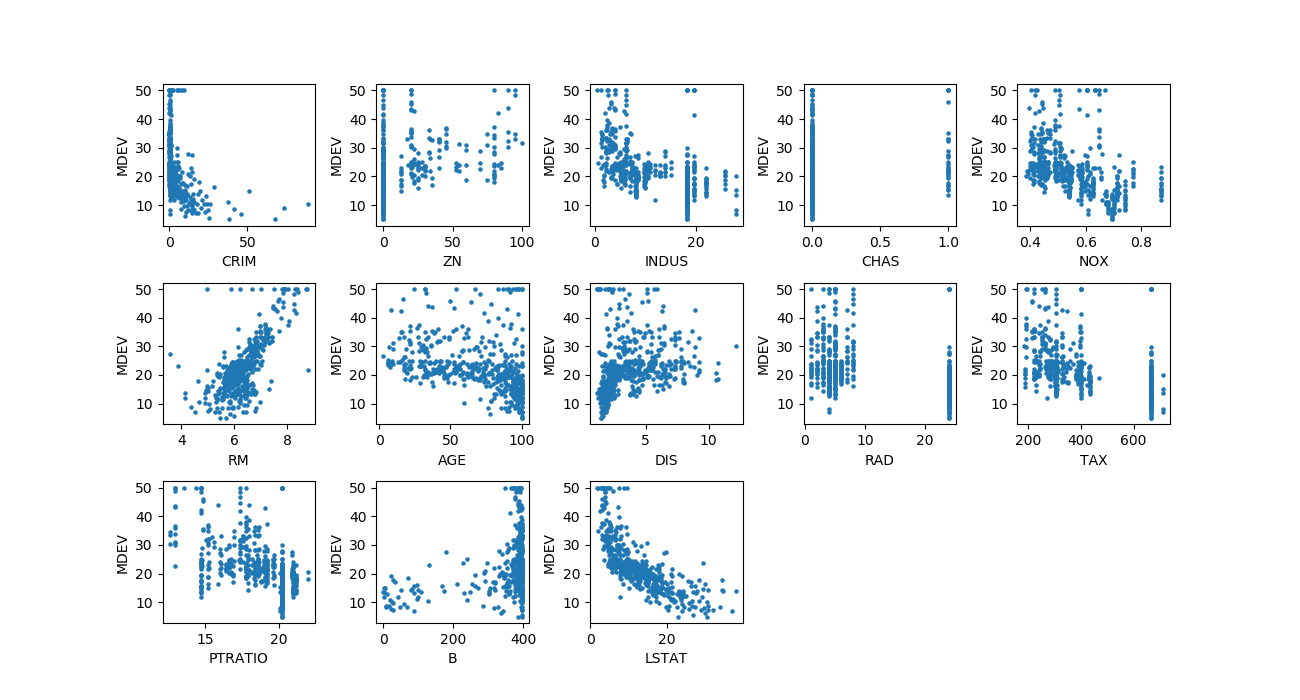
適用対象となる問題
ロジスティック回帰(Logistic regression)は「回帰」という名称だが、その機能は2クラス分類である。複数の特徴量に対して、2つのクラス1/0の何れになるかを判定する。
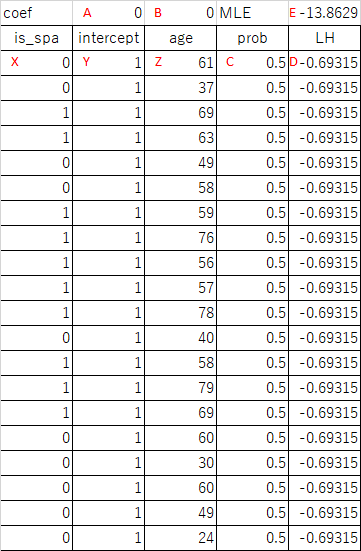
たとえば旅行会社の会員顧客20人の年齢と、温泉(SPA)とレジャーランド(LSR)のどちらを選んだかというデータが以下のように得られているとき、新たな顧客にどちらを勧めればよいか、といったような問題。
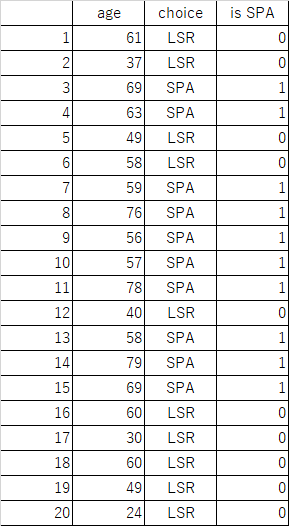
上のデータの”is SPA”列は、温泉を選んだ場合に1、レジャーランドを選んだ場合に0としている。これを散布図にすると以下の通り。
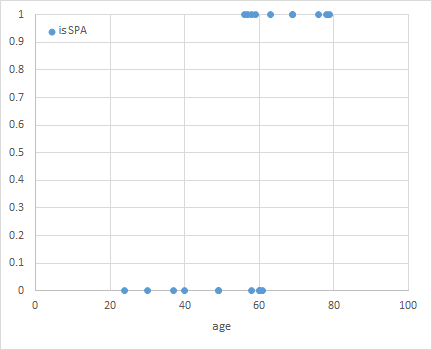
年齢が高いほど温泉を選ぶ傾向があるのは分かるが、「年齢が与えられたときに温泉とレジャーランドのどちらを選ぶか」というモデルを導出するのが目的。
(1) 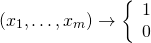
モデルを線形モデルとし、特徴量の線形和の値によってクラス1/0の何れになるかが決まるとすると
(2) 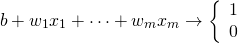
線形回帰による場合
ここでそのままデータに対して線形回帰を適用して、たとえば回帰式の値0.5に対する年齢を境にして温泉とレジャーランドを判定してもよさそうに見える。ただ、この時の回帰式がデータに対してどのような意味を持つのかが定かではない。
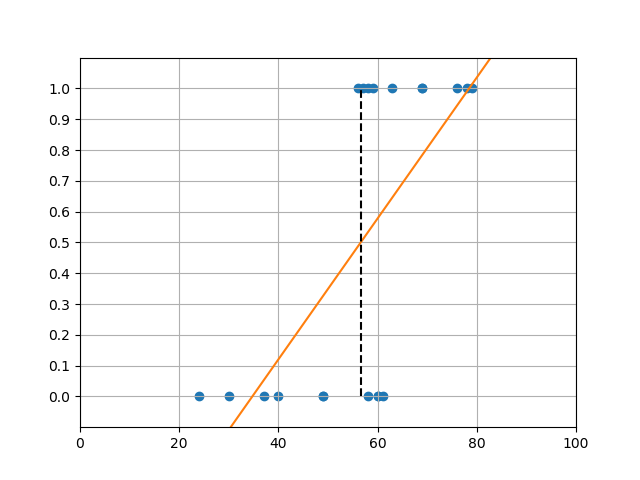
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import os import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression path = os.path.join(os.path.dirname(__file__), "data_spa.csv") df = pd.read_csv(path) X = np.array(df['age']).reshape(-1, 1) y = df['is_spa'] linreg = LinearRegression() linreg.fit(X, y) b = linreg.intercept_ w = linreg.coef_[0] x_border = (0.5 - b) / w print(x_border) xl = 0 xr = 100 yl = b + w * xl yr = b + w * xr fig, ax = plt.subplots() ax.scatter(X, y, c='tab:blue') ax.plot([xl, xr], [yl, yr], c='tab:orange') ax.plot([x_border, x_border], [0, 1], c='k', linestyle='dashed') ax.set_xlim(xl, xr) ax.set_ylim(-0.1, 1.1) ax.set_yticks(np.linspace(0, 1, 11)) ax.grid(True) plt.show() |
確率分布の仮定
単純な線形回帰ではなく、特徴量の線形和に対してクラス1となる確率分布を考える。
(3) 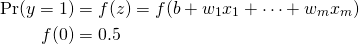
このときの確率分布の関数形として以下が必要となる。
- xの(−∞, +∞)の範囲に対して、値が(0, 1)となる
- xが小さい→確率が0に近くなる→クラス0と判別されやすくなる
- xが大きい→確率が1に近くなる→クラス1と判別されやすくなる
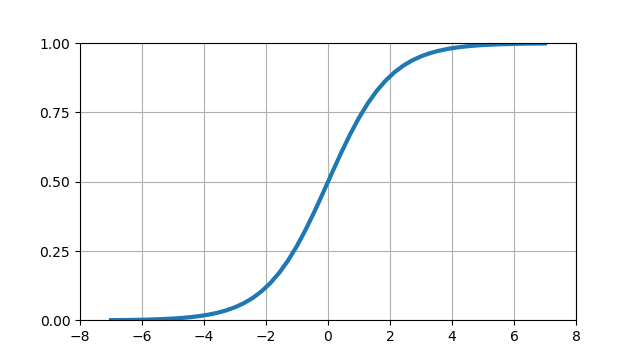
これをグラフにすると、以下のような形になる。
このような関数の回帰によるクラス分類は、確率分布に用いる関数形からLogistic回帰と呼ばれている。
Logistic回帰の定式化
確率分布関数の仮定
説明変数が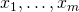 であり、それに対してある事象が発生する/発生しないの2通りがあるとする。
であり、それに対してある事象が発生する/発生しないの2通りがあるとする。
いま、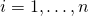 の観察対象について
の観察対象について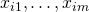 のデータが観測されたとする。このとき、以下のように定式化する。
のデータが観測されたとする。このとき、以下のように定式化する。
(4) 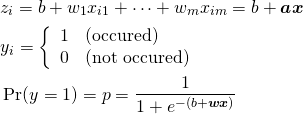
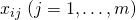 が得られたとき、その多項式を使った確率によって事象が発生することを意味している。この確率分布の式はLogistic関数と呼ばれる。
が得られたとき、その多項式を使った確率によって事象が発生することを意味している。この確率分布の式はLogistic関数と呼ばれる。
ロジスティック関数(logistic function)はシグモイド関数(sigmoid function)とも呼ばれ、その値は(0, 1)の間にあることから確率分布として採用している。
(5) 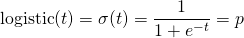
なお、ロジスティック関数の逆関数はロジット関数(logit function)と呼ばれる。
(6) 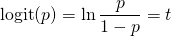
ここでLogit関数の対数の中はオッズの形になっている。
最尤推定
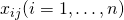 のm×n個の説明変数データと、
のm×n個の説明変数データと、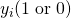 のターゲットデータが得られたとする。
のターゲットデータが得られたとする。
このとき、ターゲットデータが得られたパターンとなる確率は、それぞれが独立事象であるとすれば確率の積になるから、
(7) 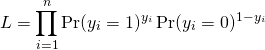
この確率は、パラメーター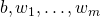 に対する尤度関数であり、その対数尤度関数は以下のようになる。
に対する尤度関数であり、その対数尤度関数は以下のようになる。
(8) 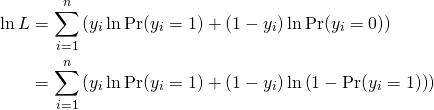
ここで、
(9) 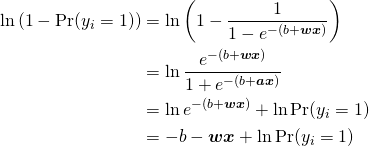
これを使って、対数尤度関数は以下のように変形される。
(10) 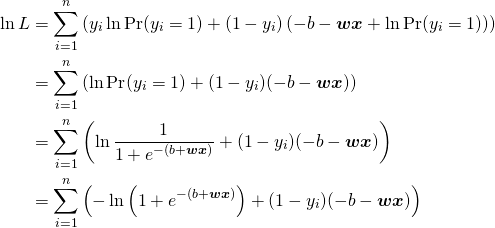
得られたデータに対してこの対数尤度を最大とするような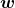 を求めるのには、通常数値計算が用いられる。
を求めるのには、通常数値計算が用いられる。
1変数の場合
定式化
線形表現は以下のようになる。
(11) 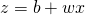
ロジスティック関数による確率表現は
(12) 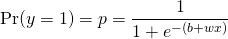
nこのデータセット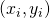 が与えられたとき、この確率分布に関する尤度関数は
が与えられたとき、この確率分布に関する尤度関数は
(13) 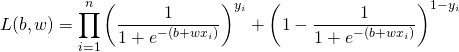
その対数尤度関数は
(14) 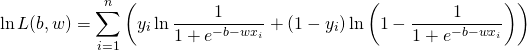
ここでデータセット(xi, yi)として、が与えられたとき、対数尤度を最大とするようなb, wを計算する。
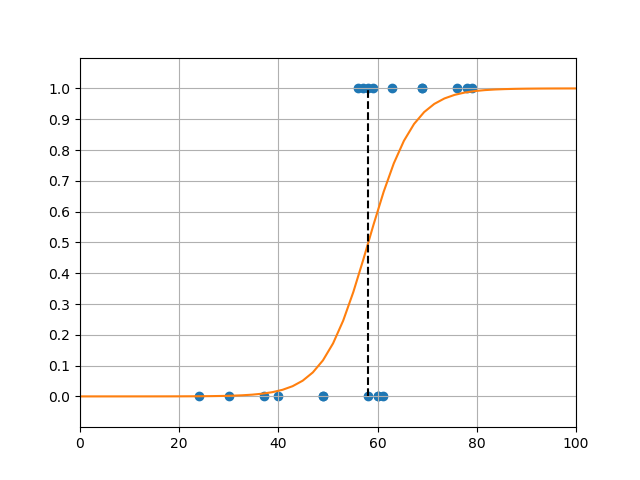
LogisticRegressionモデル
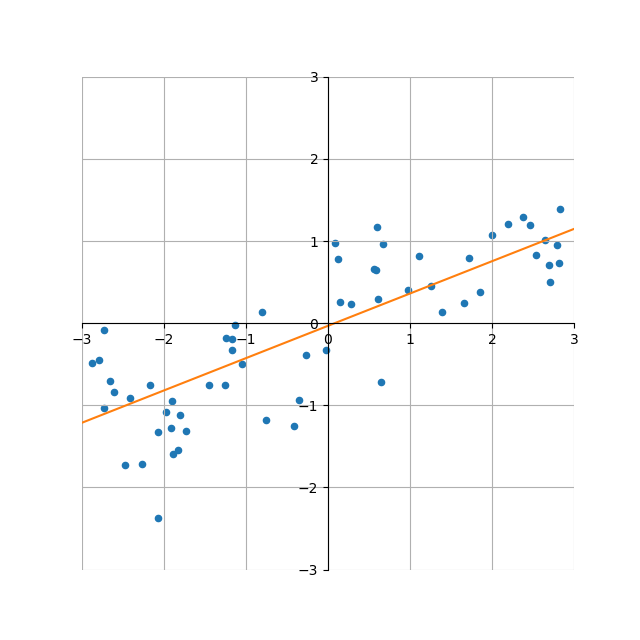
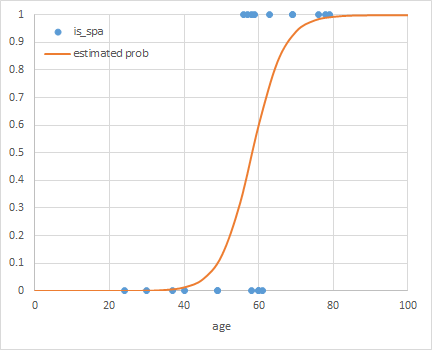
温泉のデータセットに対して、scikit-learnのLogisticRegressionモデルを適用した結果が冒頭のグラフで、コードは以下の通り。
LogisticRegressionのコンストラクターの引数としてsolver='lbfgs'を指定しているが、2020年4月時点ではこれを指定しないと警告が出るため。収束アルゴリズムにはいくつかの種類があって、データサイズや複数クラス分類・1対他分類の別などによって使い分けるようだ。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
import os import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.linear_model import LogisticRegression path = os.path.join(os.path.dirname(__file__), "data_spa.csv") df = pd.read_csv(path) X = np.array(df['age']).reshape(-1, 1) y = df['is_spa'] logreg = LogisticRegression(C=1e5, solver='lbfgs') logreg.fit(X, y) b = logreg.intercept_[0] w = logreg.coef_[0][0] x_border = 0.0 - b / w print("intercept : {}".format(b)) print("coefficient: {}".format(w)) print("x_border : {}".format(x_border)) xl = 0 xr = 100 x_graph = np.linspace(xl, xr) y_graph = 1 / (1 + np.exp(- b - w * x_graph)) fig, ax = plt.subplots() ax.scatter(X, y, c='tab:blue') ax.plot(x_graph, y_graph, c='tab:orange') ax.plot([x_border, x_border], [0, 1], c='k', linestyle='dashed') ax.set_xlim(xl, xr) ax.set_ylim(-0.1, 1.1) ax.set_yticks(np.linspace(0, 1, 11)) ax.grid(True) plt.show() # intercept : -13.44995797571776 # coefficient: 0.23116842117614878 # x_border : 58.18250566961732 |
また、同じデータセットについてExcelで解いた例はこちら。
正則化
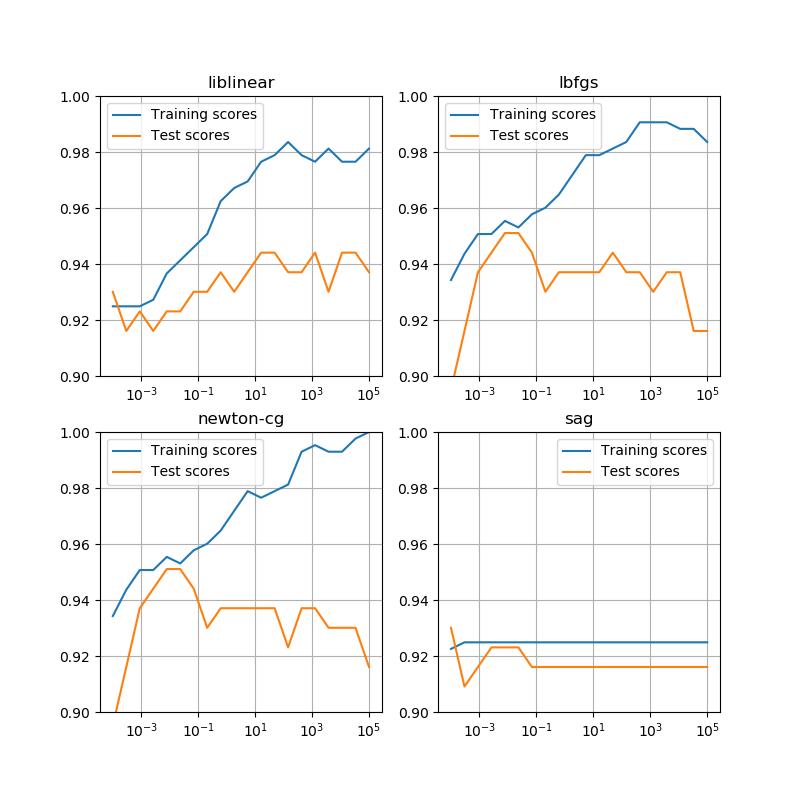
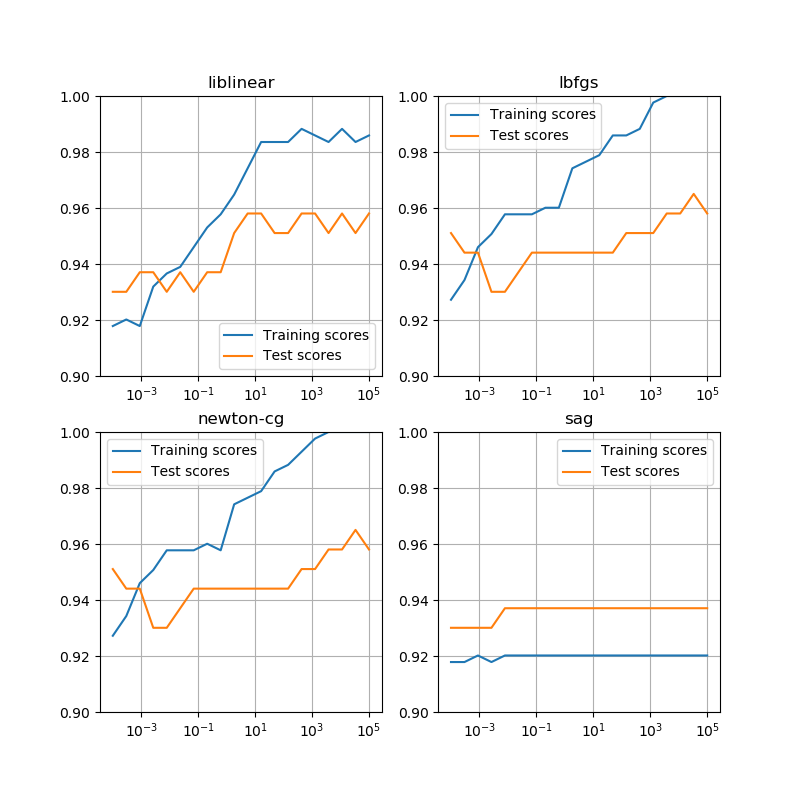
LogisticeRegressionモデルのコンストラクターの引数Cは正則化の強さを正の実数で指定する。大きな値を設定するほど正則化が弱く、小さくするほど正則化が効いてくる。
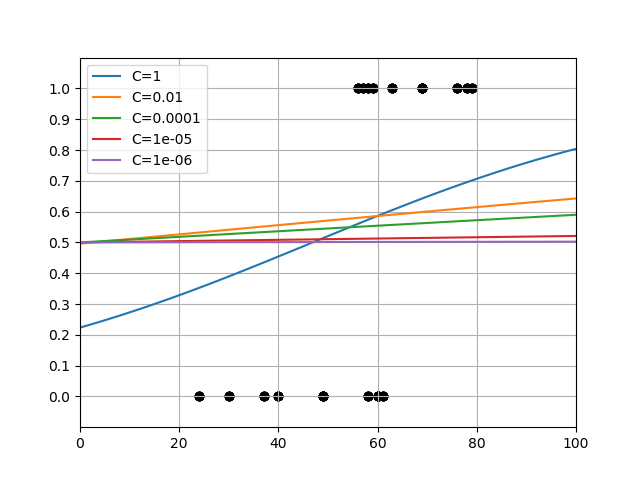
温泉のデータセットに対してCを変化させてみたところ、1000あたりから上はほとんど関数形が変わらず、ほぼ正則化がない状態。デフォルトのC=1(赤い線)は結構強い正則化のように思える。
興味深いのはこれらのグラフがほぼ1点で交わっており、その点での確率が0.6近いことである。温泉かレジャーランドかを選ぶ年齢と確率が正則化の程度に寄らず一定だということになるが、これが何を意味しているか、今のところよくわからない。
一方で、確率0.5に相当する年齢は正則化を強めていくにしたがって低くなっていて、これを判定基準とするとC=0.001ではほぼ全年齢で温泉が選択されることになってしまう。
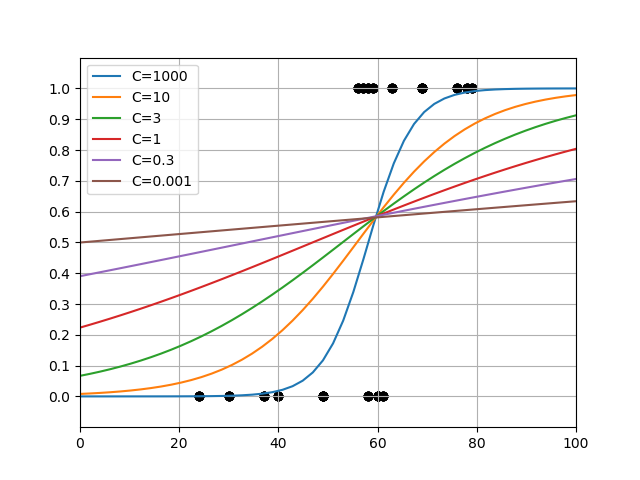
さらにCが更に小さい値になると、確率曲線はどんどんなだらかになっていき、C=1e-6では全年齢にわたって0.5、すなわち温泉、レジャーランドのいずれを選ぶかは年齢に関わらず1/2の賭けのようになっている。
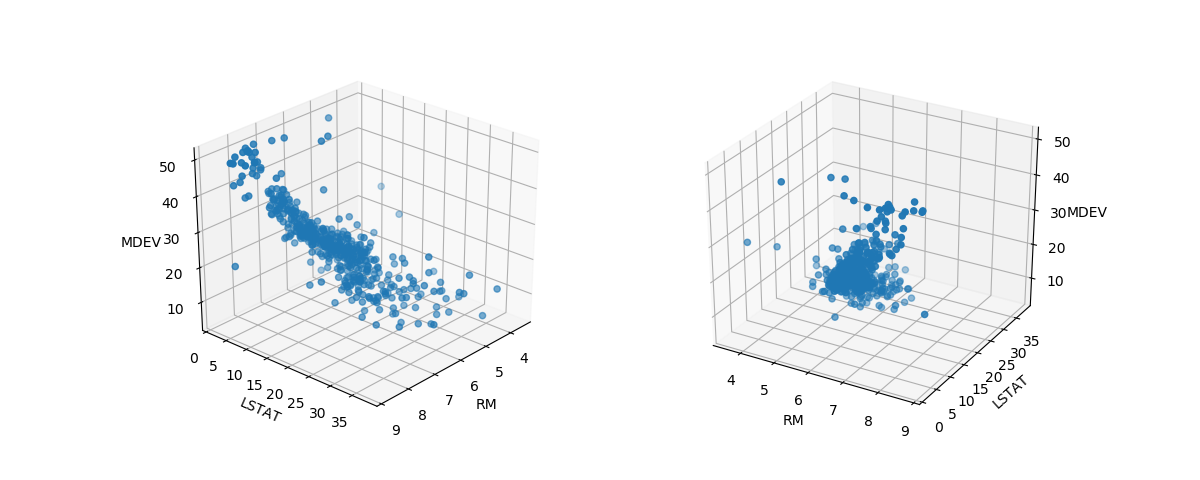
2変数の場合
2変数の例として、”O’REILLYの”Pythonではじめる機械学習”にあるforgeデータの例をトレースしたものをまとめた。
Logistic回帰~forgeデータ~Pythonではじめる機械学習より
特徴量の係数
式(4)によるとziの値が大きいほどy = 1となる確率が高くなり、小さいほどy = 0となる確率が高くなる。また、特徴量xi ≥ 0とすると、係数wiが正のときにはziを増加させる効果、負の時にはziを減少させる効果がある。y = 0, 1にターゲット0, 1が割り当てられ、それらがクラス0、クラス1を表すとすると、係数が正のときにはその特徴量の増加がクラス1を選択する方向に働き、係数が負の時にはクラス0をを選択する方向に働く。
以下は特徴量数2、クラス数2の簡単な例で、Feature-0は係数が正なのでクラス0を選択する確率を高め、Feature-1の係数は係数が負なのでクラス1を選択する確率を高める。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs from sklearn.linear_model import LogisticRegression X, y = make_blobs(n_samples=100, n_features=2, centers=2, random_state=9) logreg = LogisticRegression().fit(X, y) coef = logreg.coef_.reshape(logreg.coef_.size) f0 = np.linspace(-15, 3) f1 = (- logreg.intercept_ - coef[0] * f0) / coef[1] print("intercept:{}".format(logreg.intercept_)) print("coef:{}".format(coef)) fig, ax = plt.subplots() ax.scatter(X[y==0][:, 0], X[y==0][:, 1], label="Class-0") ax.scatter(X[y==1][:, 0], X[y==1][:, 1], label="Class-1") ax.plot(f0, f1, c='g') ax.set_xlim(-14, 4) ax.set_ylim(-12, 6) ax.set_xlabel("Feature-0") ax.set_ylabel("Feature-1") ax.legend() plt.show() # intercept:[2.11704743] # coef:[ 0.89424625 -0.66371147] |
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{x} = \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-ca095fba05bd6b51953489329a4dbed5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{X} = \left[ \begin{array}{ccc} x_{11} & \ldots & x_{1n} \\ \vdots & x_{ij} & \vdots \\ x_{m1} & \ldots & x_{mn} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-b789d485dcbf0314d7147eaf2ac533f1_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{f}(x) = \left[ \begin{array}{c} f_1(x) \\ \vdots \\ f_n(x) \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-0c143adda5de76e2ad2d9f369b269daa_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{f}(\boldsymbol{x}) =\ \left[ \begin{array}{c} f_1(x_1, \ldots, x_n) \\ \vdots \\ f_m(x_1, \ldots, x_n) \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e1402f4bca526f4e708673a396a76432_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{F}(x) = \left[ \begin{array}{ccc} F_{11}(x) & \ldots & F_{1n}(x) \\ \vdots & F_{ij} & \vdots \\ F_{m1}(x) & \ldots & F_{mn}(x) \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-11b648294a10e1e0bd969847ac5eca32_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d \boldsymbol{f}(x)}{dx} = \left[ \begin{array}{c} \dfrac{d f_1(x)}{dx} \\ \vdots \\ \dfrac{d f_n(x)}{dx} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-2a6538c824acdcefdc708eecff19c4c9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d \boldsymbol{F}(x)}{dx} = \left[ \begin{array}{ccc} \dfrac{dF_{11}(x)}{dx} & \ldots & \dfrac{dF_{1n}(x)}{dx} \\ \vdots & \dfrac{dF_{ij}(x)}{dx} & \vdots \\ \dfrac{dF_{m1}(x)}{dx} & \ldots & \dfrac{dF_{mn}(x)}{dx} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-fcd4c19cbe8c45de7a76c60b7e7414be_l3.png)
![]() のベクトルで微分すると、同じ次数のベクトルになる。
のベクトルで微分すると、同じ次数のベクトルになる。![Rendered by QuickLaTeX.com \begin{equation*} \frac{df(\boldsymbol{x})}{d\boldsymbol{x}} = \left[ \begin{array}{c} \dfrac{\partial f}{\partial x_1} \\ \vdots \\ \dfrac{\partial f}{\partial x_m} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-91df3f7d18edb4fce8d49b885fd8ba4d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{x}}f(\boldsymbol{x}) = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array}\right] f(\boldsymbol{x}) \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-4f4019636c967a53d820033d665ac0e0_l3.png)
![]() の行列で微分すると、同じ次元・次数の行列になる。
の行列で微分すると、同じ次元・次数の行列になる。![Rendered by QuickLaTeX.com \begin{equation*} \frac{df(\boldsymbol{X})}{d\boldsymbol{X}} = \left[ \begin{array}{ccc} \dfrac{\partial f}{\partial x_{11}} & \ldots & \dfrac{\partial f}{\partial x_{1n}} \\ \vdots & \dfrac{\partial f}{\partial x_{ij}} & \vdots \\ \dfrac{\partial f}{\partial x_{m1}} & \ldots & \dfrac{\partial f}{\partial x_{mn}} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-420e553422141fba601f4663078d0386_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{X}} f(\boldsymbol{X}) = \\ \left[ \begin{array}{ccc} \dfrac{\partial}{\partial x_{11}} & \ldots & \dfrac{\partial}{\partial x_{1n}} \\ \vdots & \dfrac{\partial}{\partial x_{ij}} & \vdots \\ \dfrac{\partial}{\partial x_{m1}} & \ldots & \dfrac{\partial}{\partial x_{mn}} \\ \end{array} \right] f(\boldsymbol{X}) \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-99d9e67383e94425fcf5d01ea0223e26_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d\boldsymbol{f}(\boldsymbol{x})^T}{d\boldsymbol{x}} = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \ldots & \dfrac{\partial f_n}{\partial x_1} \\ \vdots & \dfrac{\partial f_j}{\partial x_i} & \vdots \\ \dfrac{\partial f_1}{\partial x_m} & \ldots & \dfrac{\partial f_n}{\partial x_m} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-311d88dd2427ed7067a39ffafa8dad8d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{x}} \boldsymbol{f}(\boldsymbol{x})^T = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\parial}{\partial x_m} \end{array} \right] [ f_1(\boldsymbol{x}) \; \ldots \; f_n(\boldsymbol{x}) ] = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \cdots & \dfrac{\partial f_n}{\partial x_1} \\ & \dfrac{\partial f_j}{\partial x_i} &\\ \dfrac{\partial f_1}{\partial x_m} & \cdots & \dfrac{\partial f_n}{\partial x_m} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-9a2aab5d164571bef0094ea7f1eaf975_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \begin{align*} \frac{df}{dx_i} &= \frac{\partial f}{\partial u_1}\frac{\partial u_1}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_j}\frac{\partial u_j}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_n}\frac{\partial u_n}{\partial x_i} \\ \rightarrow \frac{df(\boldsymbol{u}(\boldsymbol{x}))}{d\boldsymbol{x}} &= \left[ \begin{array}{ccc} \dfrac{\partial u_1}{\partial x_1} & \cdots & \dfrac{\partial u_n}{\partial x_1} \\ \vdots && \vdots \\ \dfrac{\partial u_1}{\partial x_m} & \cdots & \dfrac{\partial u_n}{\partial x_m} \\ \end{array} \right] \left[ \begin{array}{c} \dfrac{\partial f}{\partial u_1} \\ \vdots \\ \dfrac{\partial f}{\partial u_n} \end{array} \right] \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array} \right] [u_1 \; \cdots \; u_n] \left[ \begin{array}{c} \dfrac{\partial}{\partial u_1} \\ \vdots \\ \dfrac{\partial}{\partial u_n} \end{array} \right] f(\boldsymbol{u}) \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-299db8ffb5c52904ccea0f0f44844cb4_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{align*} \frac{d(\boldsymbol{FG})}{dx} &= \frac{d}{dx}\left[\sum_{j=1}^m f_{ij} g_{jk}\right] = \left[\sum_{j=1}^m \left(\frac{df_{ij}}{dx} g_{jk} + f_{ij} \frac{dg_{jk}}{dx} \right)\right] \\ &= \left[ \sum_{j=1}^m \frac{df_{ij}}{dx} g_{jk} \right] + \left[ \sum_{j=1}^m f_{ij} \frac{dg_{jk}}{dx} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-48367a30bf2176691b7825652e570751_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} & \frac{d}{d\boldsymbol{x}} \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_j} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \\ \end{array} \right] \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{ccccc} a_{11} & \cdots & a_{i1} & \cdots & a_{m1} \\ \vdots && \vdots && \vdots \\ a_{1j} & \cdots & a_{ij} & \cdots & a_{mj} \\ \vdots && \vdots && \vdots \\ a_{1n} & \cdots & a_{in} & \cdots & a_{mn} \\ \end{array} \right] = \boldsymbol{A}^T \end{align} \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-ae74fc9540924803afe8d58422df0a6f_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \end{array} \right] [ x_1^2 + \cdots + x_n^2 ] = \left[ \begin{array}{c} 2x_1 \\ \vdots \\ 2x_n \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-9a4a53d35d99be2161876f0ebea4b973_l3.png)
![]() は正方行列で、
は正方行列で、![]() と同じ次数でなければならない。
と同じ次数でなければならない。![]()
![Rendered by QuickLaTeX.com \begin{align*} &\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] \right)\\ &=\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} a_{11} x_1 + \cdots + a_{1n} x_n \\ \vdots \\ a_{n1} x_1 + \cdots + a_{nn} x_n \end{array} \right] \right)\\ &= \frac{d}{d \boldsymbol{x}} \left( \left( a_{11} {x_1}^2 + \cdots + a_{1n} x_1 x_n \right) + \cdots + \left( a_{n1} x_n x_1 + \cdots + a_{nn} {x_n}^2 \right) \right) \end{array}\\ &=\left[ \begin{array}{c} \left( 2 a_{11} x_1 + \cdots + a_{1n} x_n \right) + a_{21} x_2 + \cdots + a_{n1} x_n \\ \vdots \\ a_{1n} x_1 + \cdots + a_{1n-1} x_{n-1} + \left( a_{n1} x_1 + \cdots + 2a_{nn} x_n \right) \end{array} \right] \\ &=\left[ \begin{array}{c} \left( a_{11} x_1 + \cdots + a_{1n} x_1 \right) + \left( a_{11} x_1 + \cdots + a_{n1} x_n \right) \\ \vdots \\ \left( a_{n1} x_1 + \cdots + a_{nn} x_n \right) + \left( a_{1n} x_1 + \cdots + a_{nn} x_n \right) \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-deafe332adeef9ea5b9eb9c5cfbd1ef5_l3.png)
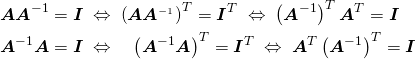
![Rendered by QuickLaTeX.com \begin{align*} \left( [ \boldsymbol{AB} ]_{ij} \right)^T = \left( \sum_k \boldsymbol{A}_{ik} \boldsymbol{B}_{kj} \right)^T = \sum_k \boldsymbol{B}_{jk} \boldsymbol{A}_{ki} =\boldsymbol{B}^T \boldsymbol{A}^T \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e0a675c84ad11bc2c66bd764f6b3dfeb_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{m1} \\ \vdots & & \vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-47268abd1fb09618f4ac57dcd0edb815_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = x_1^2 + \cdots + x_n^2 \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d7eb4031678ac7ca0faa0eefd7cb4318_l3.png)