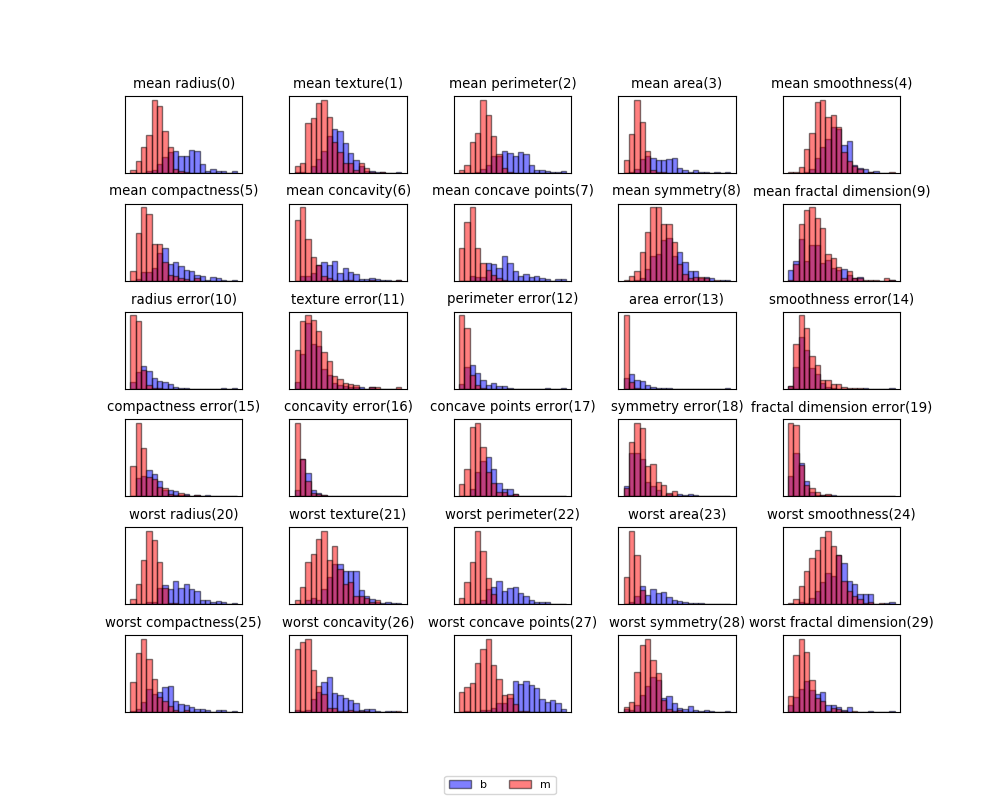
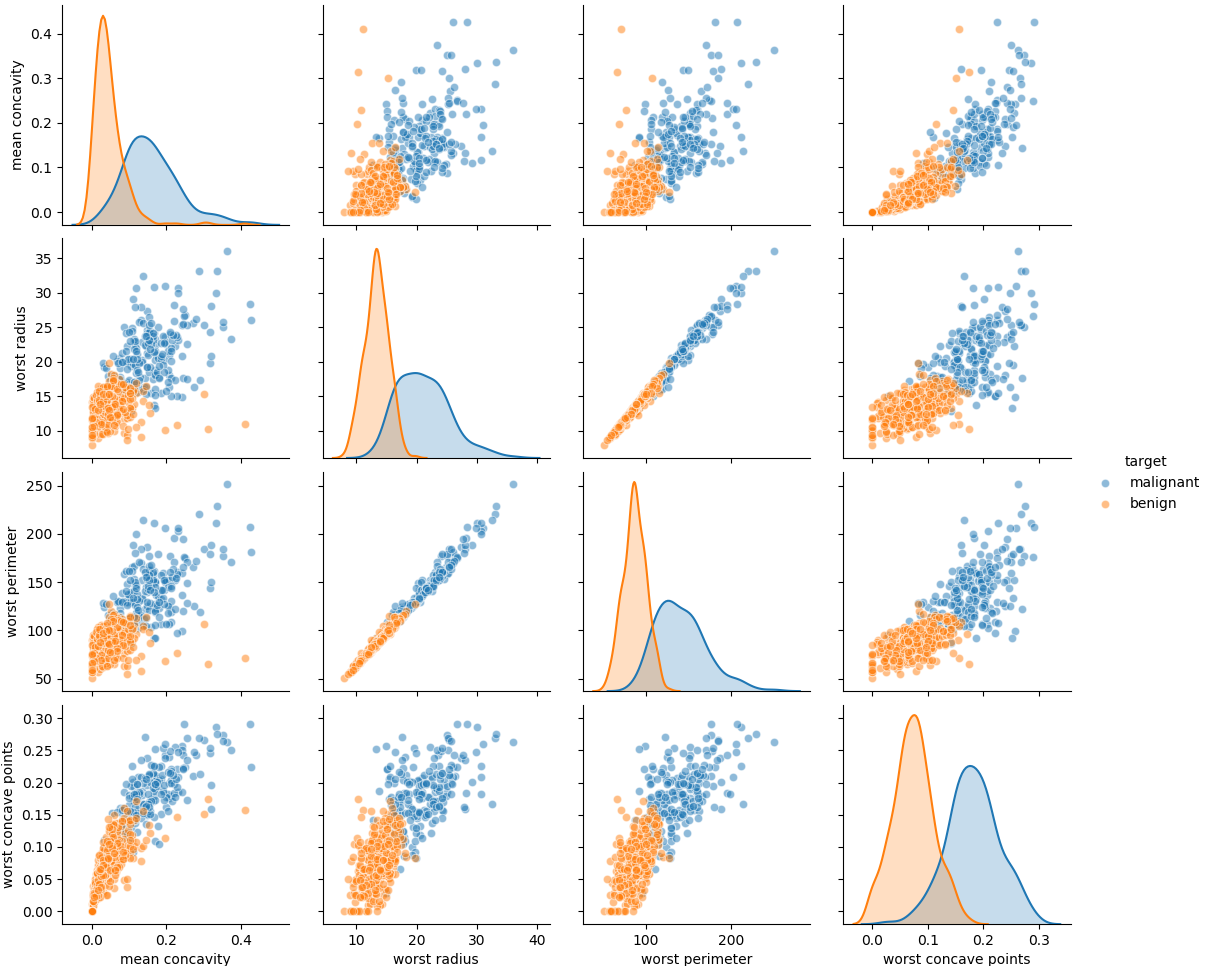
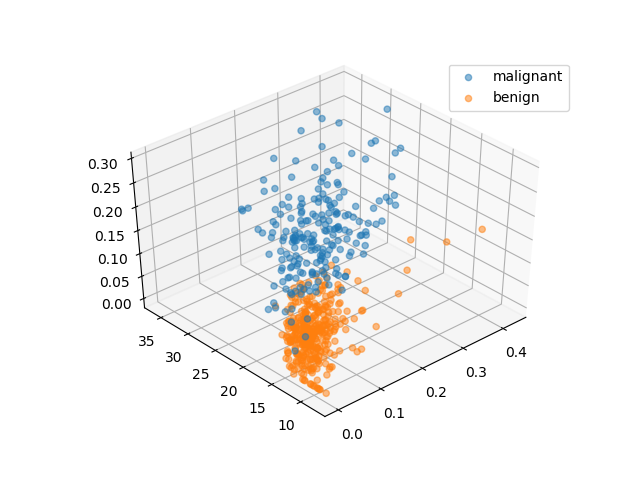
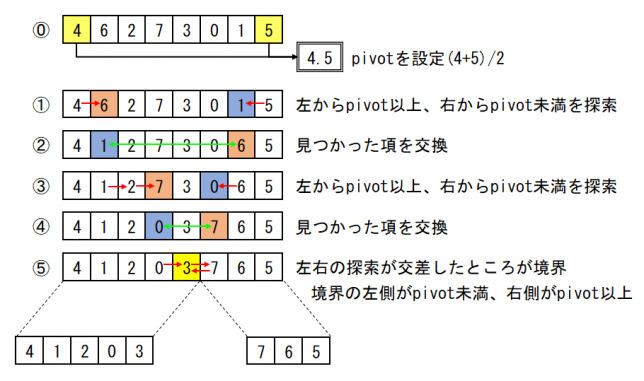
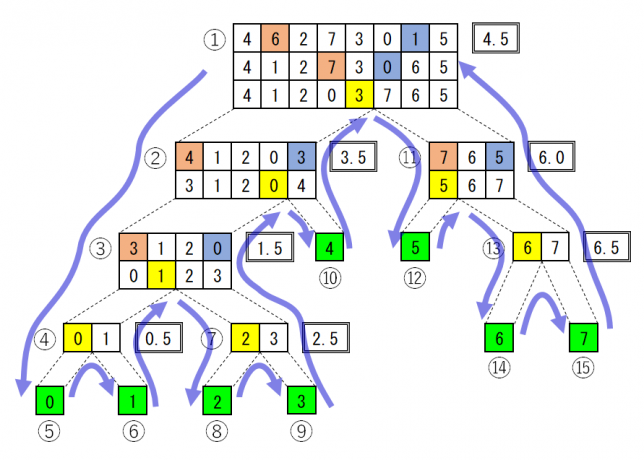
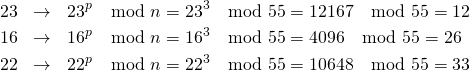function start
[4, 6, 2, 7, 3, 0, 1, 5] pivot 4.5 <- 4 5
[4, 6, 2, 7, 3, 0, 1, 5] 4.5 check 4 5
[4, 6, 2, 7, 3, 0, 1, 5] left+1 -> 6
[4, 6, 2, 7, 3, 0, 1, 5] right-1 -> 1
[4, 1, 2, 7, 3, 0, 6, 5] switched 1 6
[4, 1, 2, 7, 3, 0, 6, 5] 4.5 check 1 6
[4, 1, 2, 7, 3, 0, 6, 5] left+1 -> 2
[4, 1, 2, 7, 3, 0, 6, 5] left+1 -> 7
[4, 1, 2, 7, 3, 0, 6, 5] right-1 -> 0
[4, 1, 2, 0, 3, 7, 6, 5] switched 0 7
[4, 1, 2, 0, 3, 7, 6, 5] 4.5 check 0 7
[4, 1, 2, 0, 3, 7, 6, 5] left+1 -> 3
[4, 1, 2, 0, 3, 7, 6, 5] left+1 -> 7
[4, 1, 2, 0, 3, 7, 6, 5] right-1 -> 3
7 >= 3 border= 3
function start
[4, 1, 2, 0, 3] pivot 3.5 <- 4 3
[4, 1, 2, 0, 3] 3.5 check 4 3
[3, 1, 2, 0, 4] switched 3 4
[3, 1, 2, 0, 4] 3.5 check 3 4
[3, 1, 2, 0, 4] left+1 -> 1
[3, 1, 2, 0, 4] left+1 -> 2
[3, 1, 2, 0, 4] left+1 -> 0
[3, 1, 2, 0, 4] left+1 -> 4
[3, 1, 2, 0, 4] right-1 -> 0
4 >= 0 border= 0
function start
[3, 1, 2, 0] pivot 1.5 <- 3 0
[3, 1, 2, 0] 1.5 check 3 0
[0, 1, 2, 3] switched 0 3
[0, 1, 2, 3] 1.5 check 0 3
[0, 1, 2, 3] left+1 -> 1
[0, 1, 2, 3] left+1 -> 2
[0, 1, 2, 3] right-1 -> 2
[0, 1, 2, 3] right-1 -> 1
2 >= 1 border= 1
function start
[0, 1] pivot 0.5 <- 0 1
[0, 1] 0.5 check 0 1
[0, 1] left+1 -> 1
[0, 1] right-1 -> 0
1 >= 0 border= 0
function start
[0] return
function start
[1] return
function start
[2, 3] pivot 2.5 <- 2 3
[2, 3] 2.5 check 2 3
[2, 3] left+1 -> 3
[2, 3] right-1 -> 2
3 >= 2 border= 2
function start
[2] return
function start
[3] return
function start
[4] return
function start
[7, 6, 5] pivot 6.0 <- 7 5
[7, 6, 5] 6.0 check 7 5
[5, 6, 7] switched 5 7
[5, 6, 7] 6.0 check 5 7
[5, 6, 7] left+1 -> 6
[5, 6, 7] right-1 -> 6
[5, 6, 7] right-1 -> 5
6 >= 5 border= 5
function start
[5] return
function start
[6, 7] pivot 6.5 <- 6 7
[6, 7] 6.5 check 6 7
[6, 7] left+1 -> 7
[6, 7] right-1 -> 6
7 >= 6 border= 6
function start
[6] return
function start
[7] return
[0, 1, 2, 3, 4, 5, 6, 7]