PCA – 主成分分析

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

fig, axes = plt.subplots(2, 5, figsize=(6.4, 2.4),
    subplot_kw={'xticks':(), 'yticks':()})

fig.subplots_adjust(hspace=0.4)

for target, image, axis in zip(ds.target, ds.images, axes.ravel()):
    axis.imshow(image, cmap='gray')
    axis.set_title(ds.target_names[target], fontsize=8)

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_lfw_people

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

fig, axes = plt.subplots(2, 5, figsize=(6.4, 2.4),

subplot_kw={'xticks':(), 'yticks':()})

fig.subplots_adjust(hspace=0.4)

for target, image, axis in zip(ds.target, ds.images, axes.ravel()):

axis.imshow(image, cmap='gray')

axis.set_title(ds.target_names[target], fontsize=8)

plt.show()

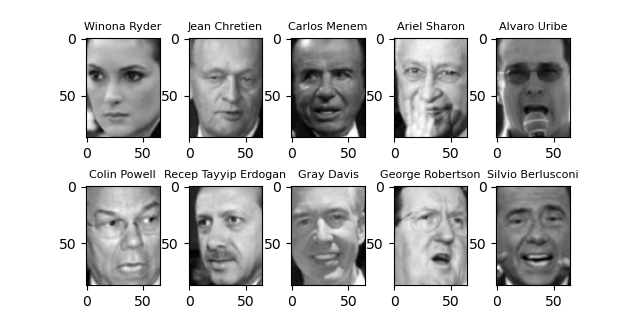
画像の人物は書籍と同じだが顔画像は異なっている。書籍執筆後画像データが追加／変更されたものと思われる。

画像の枚数の絞り込み

元のコード

LFW peopleの画像データは、人物によって枚数にばらつきがある（特にGeorge Bushだけ500枚を超えている）。画像データの多寡によるばらつきを抑えるため、書籍では画像の数を50枚までとし、それ以上の画像は切り落としている。

このコードがちょっとわかり難かったので、別にこちらで整理している。

import numpy as np
from sklearn.datasets import fetch_lfw_people

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

print(X_people.shape)
# (2063, 5655)

print(y_people.shape)
# (2063,)

print(X_people)
# [[0.22091503 0.23660131 0.30457515 ... 0.06928104 0.06666667 0.08888888]
#  [0.2627451  0.31764707 0.3477124  ... 0.03398693 0.03267974 0.03660131]
#  [0.07450981 0.05882353 0.05882353 ... 0.08888888 0.08888888 0.10065359]
#  ...
#  [0.13986929 0.0875817  0.10849673 ... 0.05751634 0.02614379 0.02091503]
#  [0.2130719  0.25882354 0.22091503 ... 0.82222223 0.82483655 0.8326797 ]
#  [0.43529412 0.50326794 0.57124186 ... 0.05359477 0.05359477 0.05490196]]

print(y_people)
# [61 25  9 ...  9 37 22]

import numpy as np

from sklearn.datasets import fetch_lfw_people

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

print(X_people.shape)

# (2063, 5655)

print(y_people.shape)

# (2063,)

print(X_people)

# [[0.22091503 0.23660131 0.30457515 ... 0.06928104 0.06666667 0.08888888]

# [0.2627451 0.31764707 0.3477124 ... 0.03398693 0.03267974 0.03660131]

# [0.07450981 0.05882353 0.05882353 ... 0.08888888 0.08888888 0.10065359]

# ...

# [0.13986929 0.0875817 0.10849673 ... 0.05751634 0.02614379 0.02091503]

# [0.2130719 0.25882354 0.22091503 ... 0.82222223 0.82483655 0.8326797 ]

# [0.43529412 0.50326794 0.57124186 ... 0.05359477 0.05359477 0.05490196]]

print(y_people)

# [61 25 9 ... 9 37 22]

k-近傍法との組み合わせによる精度の確認

書籍では、画像を50枚以下に制限したデータについて、k-近傍法(knn)を適用したときのスコア、元データを主成分分析によって変換した場合のknnのスコアを確認している。

その過程をトレースしてみた。

画像データを最近傍データ1つで判定する1-nnの実行結果は、スコアは0.23と低い
元の画像データを100個の主成分で変換したデータに対しては、1-nnのスコアは0.31と若干向上
PCAインスタンス生成時にwhiten=Trueを指定しない場合、PCA変換後もスコアは向上しなかった

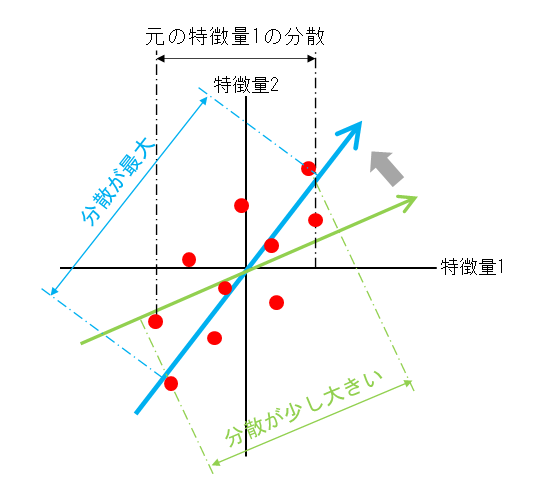
主成分の可視化

PCA.fit()を実行すると、PCA.components_に主成分が格納される。components_は2次元配列で、[主成分の数, 元の特徴量数]という形になっている。たとえば今回のデータの場合、主成分の数はn_componentsで指定した100、特徴量の数は画像のピクセル数87×65=5655となり、components_は100×5655の2次元配列になっている。

(1) $\begin{equation*} \tt{components_} = \left[ \begin{array}{ccc} (p_{0, 0} & \cdots & p_{0, 5654} ) \\ & \vdots &\\ (p_{99, 0} & \cdots & p_{99, 5654}) \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{p}_0 \\ \vdots \\ \boldsymbol{p}_{99} \end{array} \right] \end{equation*}$

components_に収められた主成分はそれぞれが画像データと同じサイズの配列なので、これらを画像として表示させてみる。

たとえばComponent-0は顔と背景のコントラスト、Component-2は顔の左右の明るさの差をコーディングしているように見える、と書籍では解説している。その他にも、Component-5は目の下の出っ張った部分、Component-11は鼻筋のあたりを表現しているかもしれないといった想像はできる。

上の画像は以下のコードで表示させたが、要点は以下の通り。

最低20枚の画像を持つ人物のみ読み込んでいる
画像の最大数を50枚以下に制限している
訓練データとテストデータに分割し、訓練データを主成分分析にかけている
components_プロパティーの主成分配列のうち、15行分を取り出して表示させている
表示にあたって、リニアな5655の要素を画像の形(87, 65)に変形している
components_の形状が、100行×5655の2次元配列であることを確認

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = ds.images[0].shape

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(
    X_people, y_people, stratify=y_people, random_state=0)

pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})
fig.subplots_adjust(hspace=0.3)

for i, (component, axis) in enumerate(zip(pca.components_, axes.ravel())):
    axis.imshow(component.reshape(image_shape))

    axis.set_title("Component-{}".format(i), fontsize=8)

plt.show()

print("image shape: {}".format(image_shape))
print("image size : {}".format(image_shape[0] * image_shape[1]))
print("components shape : {}".format(pca.components_.shape))

# image shape: (87, 65)
# image size : 5655
# components shape : (100, 5655)

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_lfw_people

from sklearn.model_selection import train_test_split

from sklearn.decomposition import PCA

from sklearn.neighbors import KNeighborsClassifier

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

image_shape = ds.images[0].shape

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(

X_people, y_people, stratify=y_people, random_state=0)

pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})

fig.subplots_adjust(hspace=0.3)

for i, (component, axis) in enumerate(zip(pca.components_, axes.ravel())):

axis.imshow(component.reshape(image_shape))

axis.set_title("Component-{}".format(i), fontsize=8)

plt.show()

print("image shape: {}".format(image_shape))

print("image size : {}".format(image_shape[0] * image_shape[1]))

print("components shape : {}".format(pca.components_.shape))

# image shape: (87, 65)

# image size : 5655

# components shape : (100, 5655)

次元圧縮された主成分からの復元

概要

主成分の意味の一つとして、元のデータは主成分の線形和で表せるという解釈がある。

(2) $\begin{equation*} \boldsymbol{x} = (x_0, ..., x_n) = a_0 \boldsymbol{p}_0 + a_1 \boldsymbol{p}_1 + a_2 \boldsymbol{p}_2 + \cdots \end{equation*}$

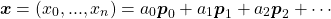
LFWの顔画像データで考えると、components_に収められた主成分の重みによって、元のそれぞれの人物の画像を再現しようとすることになる。

そこで、限られた主成分だけを用いて元の顔画像を再現してみる。

顔画像の選定

まず、特に有名な人物の顔画像をいくつか表示させてみた。選んだ人物は、Arnold Schwarzenegger, Tiger Woods, Vladimir Putinの3人。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = ds.images[0].shape

names = ['Arnold Schwarzenegger', 'Tiger Woods', 'Vladimir Putin']

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})
fig.subplots_adjust(hspace=0.3)

for name, axes_row in zip(names, axes):
    id = np.where(ds.target_names == name)[0][0]
    for image_num, axis in zip(np.where(ds.target == id)[0][:5], axes_row):
        axis.imshow(ds.images[image_num])
        axis.set_title("Image {}".format(image_num), fontsize=8)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_lfw_people

from sklearn.model_selection import train_test_split

from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

image_shape = ds.images[0].shape

names = ['Arnold Schwarzenegger', 'Tiger Woods', 'Vladimir Putin']

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})

fig.subplots_adjust(hspace=0.3)

for name, axes_row in zip(names, axes):

id = np.where(ds.target_names == name)[0][0]

for image_num, axis in zip(np.where(ds.target == id)[0][:5], axes_row):

axis.imshow(ds.images[image_num])

axis.set_title("Image {}".format(image_num), fontsize=8)

plt.show()

これらの画像から、一旦次元削減して復元する画像を選ぶ。Shwalzzeneggerは正面少し左向きの31番、Tiger Woodsは少し右側から撮った歯を出している683番、Putinは左を向いた顔をほぼ正面から撮った372番を選んだ。

次元削減後の逆変換

そして次元数を変化させながらPCAモデルに全データを学習させ、それらのモデルで3枚の画像を変形し、逆変換する。

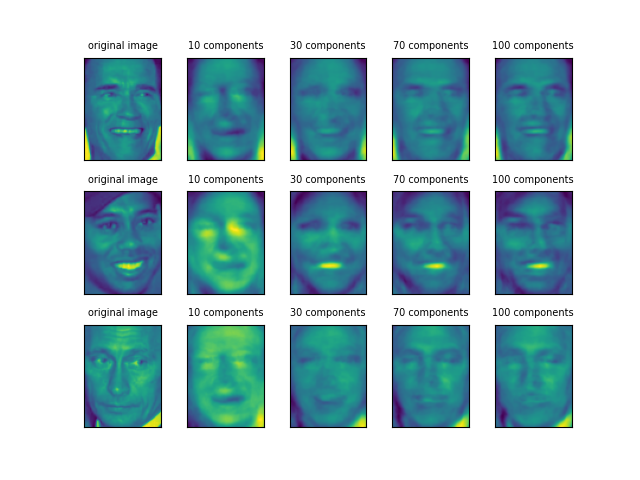
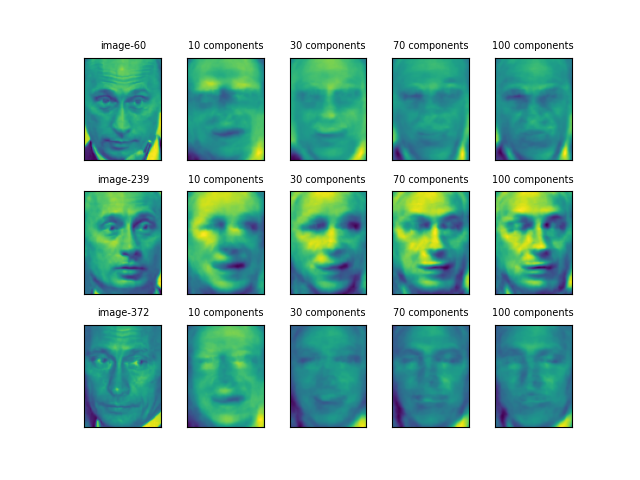
10個の主成分では、3人とも似たような顔になっているが、30個になると顔の方向や葉を出しているかどうかといった特徴が表れ始めている。

70個から100個にかけて、ShwaltzeneggerとWoodsはかなり元の顔に近いが、Putinはあまり判然としない。前者2人が「濃い」顔立ちなのに比べると、Putinの顔立ちは平板だということだろうか。

この画像は、以下の手順で作成した。

20枚以上の画像を持つ人物を選び、画像の枚数を50枚以下に制限
3人の顔画像について、次元数を10、30、70、100と変化させて以下を実行
1. 設定された次元数で全データを学習
2. 学習済みモデルで各顔画像を変換（ここで次元が削減される）
3. 設定された次元数で元の顔画像に逆変換

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = ds.images[0].shape

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

images = [31, 683, 372]
n_component_list = [10, 30, 70, 100]

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})
fig.subplots_adjust(hspace=0.3)

for r, image_id in enumerate(images):
    axes[r, 0].imshow(ds.images[image_id])
    axes[r, 0].set_title("original image", fontsize=7)

for c, n_components in enumerate(n_component_list):
    pca = PCA(n_components=n_components, whiten=True, random_state=0).fit(X_people)
    for r, image_id in enumerate(images):
        image_trans = pca.transform(ds.data[image_id].reshape(1, -1))
        image_inv = pca.inverse_transform(image_trans)
        axes[r, c + 1].imshow(image_inv.reshape(image_shape))
        axes[r, c + 1].set_title("{} components".format(n_components), fontsize=7)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_lfw_people

from sklearn.model_selection import train_test_split

from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

image_shape = ds.images[0].shape

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

images = [31, 683, 372]

n_component_list = [10, 30, 70, 100]

fig, axes = plt.subplots(3, 5, subplot_kw={'xticks':(), 'yticks':()})

fig.subplots_adjust(hspace=0.3)

for r, image_id in enumerate(images):

axes[r, 0].imshow(ds.images[image_id])

axes[r, 0].set_title("original image", fontsize=7)

for c, n_components in enumerate(n_component_list):

pca = PCA(n_components=n_components, whiten=True, random_state=0).fit(X_people)

for r, image_id in enumerate(images):

image_trans = pca.transform(ds.data[image_id].reshape(1, -1))

image_inv = pca.inverse_transform(image_trans)

axes[r, c + 1].imshow(image_inv.reshape(image_shape))

axes[r, c + 1].set_title("{} components".format(n_components), fontsize=7)

plt.show()

同一人物の画像

さらに、3人について1人ずつ、3枚の顔画像について同様のことを行った結果が以下の通り。

Shwalzeneggerの後半2枚は向きが逆だが口元などがよく似ていて、目元と口元の特徴が強調されている。1枚目の画像はこの2枚と特徴が違うが、主成分30個あたりではよく似た感じともいえる。

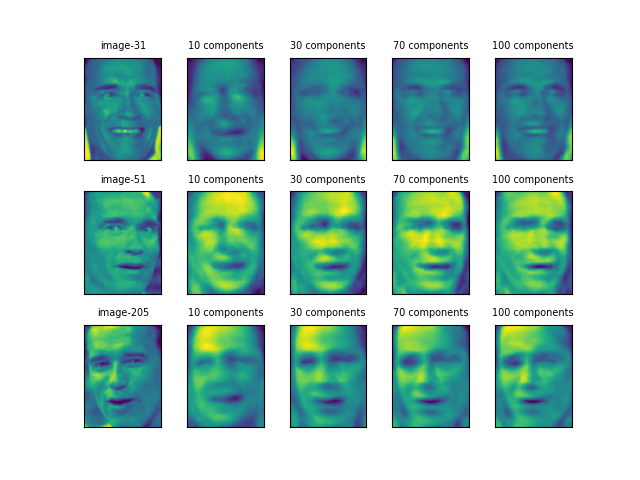
Tiger Woodsも、主成分30個のところで173と683の画像が似ている。だが、535については一貫して他の2つと異なっているように見える。個人の特徴よりも顔の表情に大きく引きずられているようだ。

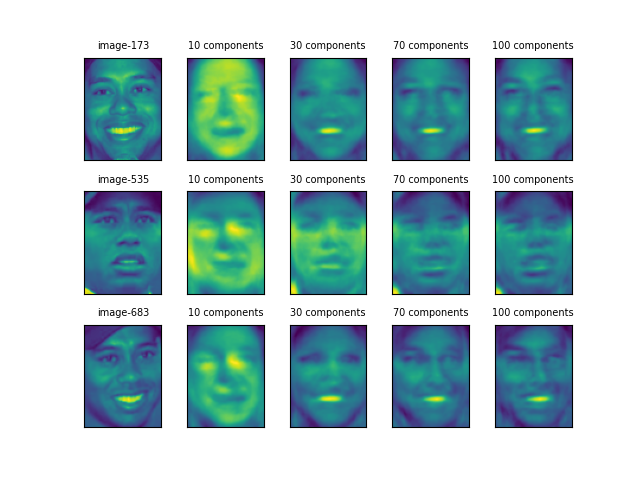
Putinは60と372の画像が割に似ているが、239の画像はかなり異なり、コントラストが強調されているようだ。60や372では、そもそも顔画像が平板なせいなのか、主成分を増やしても明確な画像が得られていない（他の人物との区別も難しいのではないだろうか）。

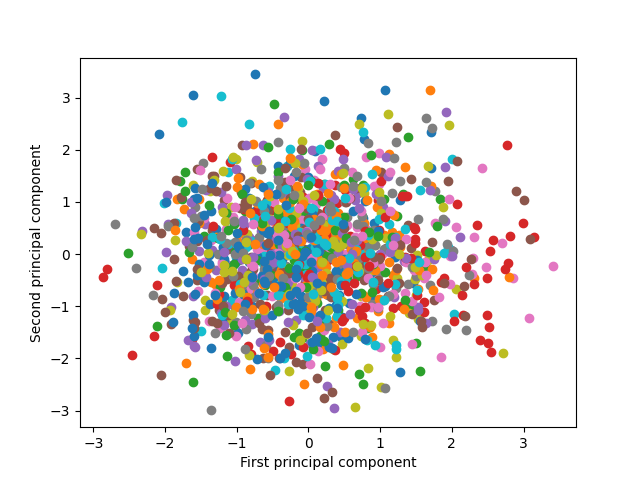
第2主成分までによるクラスの分布

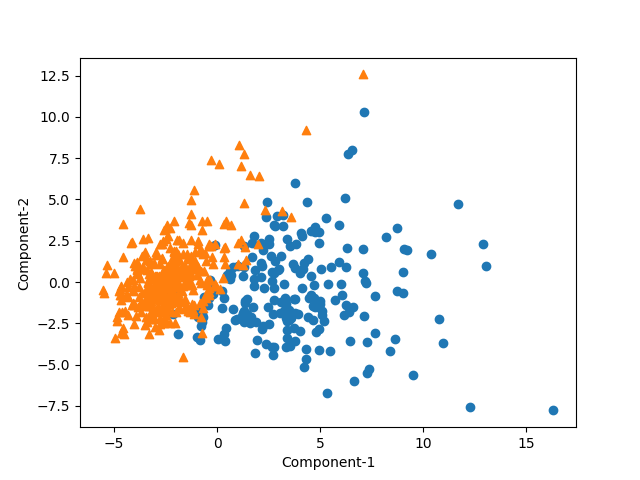
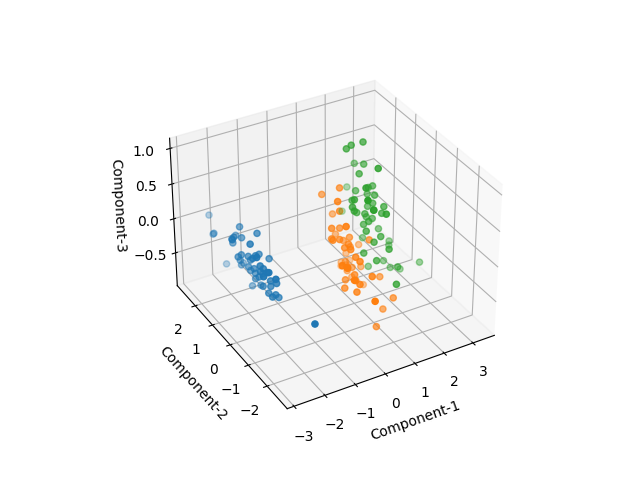
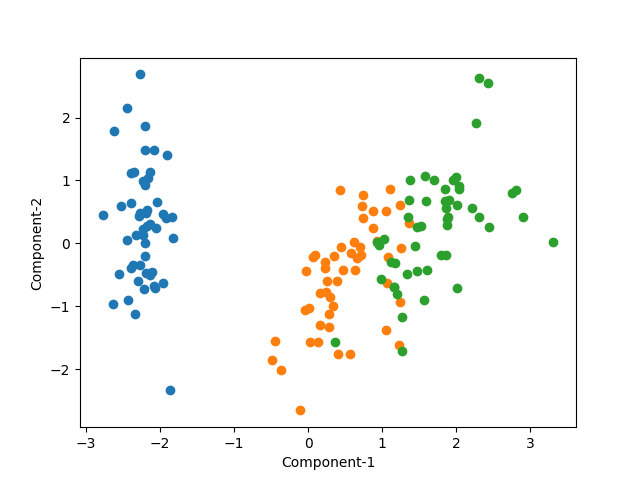
第1主成分と第2主成分だけを使って、各クラスの分布をみてみる。62人の人物の各画像データが1つの点に対応している。2つの主成分だけでは人物が明確なクラスターとしては認識し難い（というよりもクラスが多すぎて識別も難しい）。

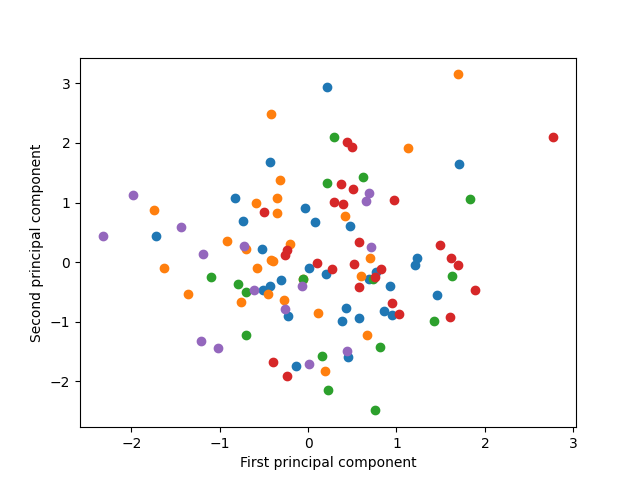
試しに表示するクラスを5つに限定してみる。やはり2つの主成分では明確なクラスターは確認できない。先ほどの変換・逆変換の結果でも、主成分10個でも個々の顔の識別は困難だったので、2つの主成分では難しいのは自明だが。

以上の可視化のコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(
    X_people, y_people, stratify=y_people, random_state=0)

pca = PCA(n_components=3, whiten=True, random_state=0).fit(X_train)

X_trans = pca.transform(X_train)

target_classes = np.unique(y_train)

fig, axis = plt.subplots()

for target_class in target_classes[:5]:
    mask = np.zeros(y_train.shape, dtype=np.bool)
    mask[np.where(y_train == target_class)] = 1
    axis.scatter(X_trans[mask, 0], X_trans[mask, 1])
    axis.set_xlabel("First principal component")
    axis.set_ylabel("Second principal component")

plt.show()

print("components_.shape : {}".format(pca.components_.shape))
print("X_train -> X_trans: {} -> {}".format(X_train.shape, X_trans.shape))
print("y_train.shape     : {}".format(y_train.shape))

# components_.shape : (3, 5655)
# X_train -> X_trans: (1547, 5655) -> (1547, 3)
# y_train.shape     : (1547,)

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_lfw_people

from sklearn.model_selection import train_test_split

from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(

X_people, y_people, stratify=y_people, random_state=0)

pca = PCA(n_components=3, whiten=True, random_state=0).fit(X_train)

X_trans = pca.transform(X_train)

target_classes = np.unique(y_train)

fig, axis = plt.subplots()

for target_class in target_classes[:5]:

mask = np.zeros(y_train.shape, dtype=np.bool)

mask[np.where(y_train == target_class)] = 1

axis.scatter(X_trans[mask, 0], X_trans[mask, 1])

axis.set_xlabel("First principal component")

axis.set_ylabel("Second principal component")

plt.show()

print("components_.shape : {}".format(pca.components_.shape))

print("X_train -> X_trans: {} -> {}".format(X_train.shape, X_trans.shape))

print("y_train.shape : {}".format(y_train.shape))

# components_.shape : (3, 5655)

# X_train -> X_trans: (1547, 5655) -> (1547, 3)

# y_train.shape : (1547,)

Python – 配列要素の重複数を制限する

2020-11-24 / tau / コメントする

概要

文字で表現するとわかり難いが、要するに次のようなことを想定している。たとえば次のような1次元の配列があるとする。

import numpy as np

np.random.seed(0)
targets = np.random.randint(0, 5, 20)

print(targets)
# [4 0 3 3 3 1 3 2 4 0 0 4 2 1 0 1 1 0 1 4]

print(np.bincount(targets))
# [5 5 2 4 4]

import numpy as np

np.random.seed(0)

targets = np.random.randint(0, 5, 20)

print(targets)

# [4 0 3 3 3 1 3 2 4 0 0 4 2 1 0 1 1 0 1 4]

print(np.bincount(targets))

# [5 5 2 4 4]

この配列には20個の要素があり、0～4の数値がそれぞれ5個、5個、2個、2個、4個、4個、順不同で含まれている。

この配列において、各数値の数を最大でも3個以内となるように切り落としたい、というのが目標。

たとえば、機械学習の教師データの数がターゲットごとにばらついている場合、各ターゲットのデータ数をある程度の数以下に抑えたいときが想定される。

上の例で仮に早く出現した準から3つまでを残して後は捨てるとすれば、以下のような配列になる。

内容：4 0 3 3 3 1 3 2 4 0 0 4 2 1 0 1 1 0 1 4
個数：1 1 1 2 3 1 4 1 2 2 3 3 2 2 4 3 4 5 5 4

なお、単に1つの配列の要素を切り落とすだけでなく、これと対応する配列が別にあって、その要素についても同時に切り落とすことも想定する。これは、機械学習のターゲット配列でデータを制限するのに、これに紐づけられた画像データなどを格納した配列も同時に操作するイメージ。

手順

ターゲットごとのインデックスの取得

targetsの20個のデータのうちid=0について考える。targetsの要素のうち値が0のものは5個あり、それらのインデックスは(1, 9, 10, 14, 17)。同様にid=1についても5個あり、インデックスは(5, 13, 15, 16, 18)。

このようにしてid=0～4についてインデックスを書き出すと以下の通りになる。

0：1, 9, 10, 14, 17
1：5, 13, 15, 16, 18
2：7, 12
3：2, 3, 4, 6
4：0, 8, 11, 19

各idに対応する配列はnumpy.where()関数を用いて以下のように得られる。

for id in range(5):
    array = np.where(targets == id)[0]
    print("{}:{}".format(id, array))

# 0:[ 1  9 10 14 17]
# 1:[ 5 13 15 16 18]
# 2:[ 7 12]
# 3:[2 3 4 6]
# 4:[ 0  8 11 19]

for id in range(5):

array = np.where(targets == id)[0]

print("{}:{}".format(id, array))

# 0:[ 1 9 10 14 17]

# 1:[ 5 13 15 16 18]

# 2:[ 7 12]

# 3:[2 3 4 6]

# 4:[ 0 8 11 19]

上の例では、ループのidを0～4と変化させていくのにrange(5)を使っている。ところが一般的には、番号が連続して存在しているとは限らず、またその上限もわからない。

そこで、targetsに出てくる要素を重なりなく、かつ全て使うためにnumpy.unique()関数を使っている。unique()関数は引数の配列の要素の重複を除き、昇順・辞書順に並べてくれる。この引数にtargetsを渡して、要素の重なりを除けば、targets中の要素を重なりなく1つずつ参照できる。

print(np.unique(targets))
# [0 1 2 3 4]

for id in np.unique(targets):
    array = np.where(targets == id)[0]
    print("{}:{}".format(id, array))

# [ 1  9 10 14 17]
# [ 5 13 15 16 18]
# [ 7 12]
# [2 3 4 6]
# [ 0  8 11 19]

print(np.unique(targets))

# [0 1 2 3 4]

for id in np.unique(targets):

array = np.where(targets == id)[0]

print("{}:{}".format(id, array))

# [ 1 9 10 14 17]

# [ 5 13 15 16 18]

# [ 7 12]

# [2 3 4 6]

# [ 0 8 11 19]

取り出す要素の制限

次に、すべてのターゲットのデータ数が3個以下になるようにすることを考える。

これらのデータで各idの個数を3個以下にするのに、出現順位の早いものから3個を選び出すことを考える。

0：1, 9, 10, 14, 17
1：5, 13, 15, 16, 18
2：7, 12
3：2, 3, 4, 6
4：0, 8, 11, 19

各配列の最初の3個を取り出すには、各idに対応する配列の先頭から3個目までをスライスで取り出せばよい。

for id in np.unique(targets):
    array = np.where(targets == id)[0][:3]
    print("{}:{}".format(id, array))

# 0:[ 1  9 10]
# 1:[ 5 13 15]
# 2:[ 7 12]
# 3:[2 3 4]
# 4:[ 0  8 11]

for id in np.unique(targets):

array = np.where(targets == id)[0][:3]

print("{}:{}".format(id, array))

# 0:[ 1 9 10]

# 1:[ 5 13 15]

# 2:[ 7 12]

# 3:[2 3 4]

# 4:[ 0 8 11]

これで値の最大3個までとするのに取り出すべきtargets中のインデックスが得られた。

要素の抽出

targets配列の要素の個数を制限するには、上で絞り込まれたインデックスに対応する要素を残し、それ以外の要素を切り捨てる。そのためには、残すべきインデックス位置の値がTrue、その他のインデックス位置の値がFalseであるbool配列をつくり、これをtargetsの引数とすればよい。

この配列を例えばmaskという名前とすると、targetsと同じサイズですべての要素がFalseである配列としてmaskを準備し、先ほどの切り落とすべきインデックスの位置のみTrueにするとよい。

以下では、まず全要素がFalseでtargetsと同じサイズのbool配列を準備し、各idに対して3つ目までの要素の位置をTrue(1)としている。

ループの1回目で1、9、10番目がTrueになり、2回目で5、13、15番目がTrueに代わっていき、ループを重ねるごとに、取り出すべき要素の位置がTrueになっていることが確認できる。

なおbool配列の初期化では、Falseが数値の0と等価なため、numpy.zeros()関数を使っている。同じ理由で、numpy.where()でTrueをセットするときに、数値の1をセットしている。

mask = np.zeros(targets.size, dtype=np.bool)
print(mask)

# [False False False False False False False False False False False False
#  False False False False False False False False]

for target in np.unique(targets):
    mask[np.where(targets == target)[0][:3]] = 1
    print(mask)

# [False  True False False False False False False False  True  True False
#  False False False False False False False False]
# [False  True False False False  True False False False  True  True False
#  False  True False  True False False False False]
# [False  True False False False  True False  True False  True  True False
#   True  True False  True False False False False]
# [False  True  True  True  True  True False  True False  True  True False
#   True  True False  True False False False False]
# [ True  True  True  True  True  True False  True  True  True  True  True
#   True  True False  True False False False False]

mask = np.zeros(targets.size, dtype=np.bool)

print(mask)

# [False False False False False False False False False False False False

# False False False False False False False False]

for target in np.unique(targets):

mask[np.where(targets == target)[0][:3]] = 1

print(mask)

# [False True False False False False False False False True True False

# False False False False False False False False]

# [False True False False False True False False False True True False

# False True False True False False False False]

# [False True False False False True False True False True True False

# True True False True False False False False]

# [False True True True True True False True False True True False

# True True False True False False False False]

# [ True True True True True True False True True True True True

# True True False True False False False False]

最後に、このbool配列をtargetsに適用して、取り出すべき要素の配列を得る。

print(targets[mask])
# [4 0 3 3 3 1 2 4 0 0 4 2 1 1]

print(np.bincount(targets[mask]))
# [3 3 2 3 3]

print(targets[mask])

# [4 0 3 3 3 1 2 4 0 0 4 2 1 1]

print(np.bincount(targets[mask]))

# [3 3 2 3 3]

他の配列の同時操作

mask配列は、targetsと同じサイズを持つ次元の配列に繰り返し適用できるので、たとえば機械学習でtargetsの各要素に紐づけられた画像データなどを格納した配列などについても、targetsと整合させながら必要な分だけ切出すことができる。

LFWデータセット – k近傍法（PCA変換付き）

2020-11-23 / tau / コメントする

概要

“Pythonではじめる機械学習”の主成分分析(PCA)のところで、著名人の顔画像データ（LFW peopleデータセット）に対するk-近傍法の精度を確認している。

LFW peopleのデータを、最低20枚以上の画像がある人物で絞り込んで読み込み
各人物の画像を最大でも50枚以内となるよう制限（配列要素数の制限手順についてはこちらを参照）
2063人の人物について、87×65ピクセルを1次元化した5,655個の数値配列を特徴量データ(X_people)、各画像の人物の番号を収めた配列(y_people)をターゲットデータとする
画像データを訓練データとテストデータに分割
このデータセットをそのまま1-nnで予測したスコアは、0.2程度でそれほどよくない
画像データに主成分分析(PCA)を用いて、100個の主成分で変換したデータについても1-nnを適用していて、この場合のスコアは0.31

コード例ではPCAインスタンス生成時の引数としてwhiten=Trueを指定しているが、これを指定しない場合、データ変換後のスコアは0.23でこうじょうしなかった。

なお、スコアが書籍掲載値と異なるが、画像データの内容も書籍と今回実行時で異なっている。

コードと実行結果

import numpy as np
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)
for target in np.unique(ds.target):
    mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]
y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(
    X_people, y_people, stratify=y_people, random_state=0)

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test score (1-nn): {:.2f}".format(knn.score(X_test, y_test)))

pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)

knn.fit(X_train_pca, y_train)
print("Test score (1-nn) w/ PCA: {:.2f}".format(knn.score(X_test_pca, y_test)))

print("\nUsed data shape")
print(X_train.shape, X_test.shape)
print(X_train_pca.shape, X_test_pca.shape)
print(y_train.shape, X_test.shape)

# Test score (1-nn): 0.23
# Test score (1-nn) w/ PCA: 0.31
# 
# Used data shape
# (1547, 5655) (516, 5655)
# (1547, 100) (516, 100)
# (1547,) (516, 5655)

import numpy as np

from sklearn.datasets import fetch_lfw_people

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsClassifier

from sklearn.decomposition import PCA

ds = fetch_lfw_people(min_faces_per_person=20, resize=0.7)

mask = np.zeros(ds.target.shape, dtype=np.bool)

for target in np.unique(ds.target):

mask[np.where(ds.target == target)[0][:50]] = 1

X_people = ds.data[mask]

y_people = ds.target[mask]

X_people /= 255

X_train, X_test, y_train, y_test = train_test_split(

X_people, y_people, stratify=y_people, random_state=0)

knn = KNeighborsClassifier(n_neighbors=1)

knn.fit(X_train, y_train)

print("Test score (1-nn): {:.2f}".format(knn.score(X_test, y_test)))

pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)

X_train_pca = pca.transform(X_train)

X_test_pca = pca.transform(X_test)

knn.fit(X_train_pca, y_train)

print("Test score (1-nn) w/ PCA: {:.2f}".format(knn.score(X_test_pca, y_test)))

print("\nUsed data shape")

print(X_train.shape, X_test.shape)

print(X_train_pca.shape, X_test_pca.shape)

print(y_train.shape, X_test.shape)

# Test score (1-nn): 0.23

# Test score (1-nn) w/ PCA: 0.31

# Used data shape

# (1547, 5655) (516, 5655)

# (1547, 100) (516, 100)

# (1547,) (516, 5655)

PCA – Boston house-pricesデータセット

2020-11-20 / tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をBiston housing pricesデータに適用して、その挙動を確認する。

主成分が適切に発見されてよい相関が得られることを期待したが、IrisデータやBreast cancerデータの場合のようなクラス分類データにおける良好な結果は得られなかった。

ただし、Boston housing pricesデータはIrisやcancerのデータよりも複雑な社会行動に関するものであり、その指標も限定されていることから、これをもってPCAが回帰系のデータに不向きとまでは言い切れない。

なお、Boston housing pricesデータの特徴量には属性データ（カテゴリーデータ、クラスデータ）が含まれることから、DataFrameのget_dummis()メソッドによるone-hot encodingを行っている。

計算の手順

必要なパッケージをインポート
Boston housing pricesデータセットを準備
データセットをスケーリング／エンコーディング
1. 属性データの列を取り出して、get_dummiesでone-hot化
2. StandardScalerで残りの特徴量データを標準化
3. 上記2つを結合して前処理済みデータとして準備
PCAモデルのインスタンスを生成
- 引数n_components=2として、2つの特徴量について計算
fit()メソッドにより、モデルにデータを学習させる
主成分やその寄与率を確認
- 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
transform()メソッドによって、主成分に沿ってデータを変換
3つの主成分について3次元可視化
2つの主成分について2次元可視化

前処理

特徴量のうちの1つCHASについては、「チャールズ川に関するダミー変数（1：川沿い、0：それ以外）」～”Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)“となっていて、0か1の属性変数である。この変数をDataFrameのget_dummies()メソッドでone-hot化する。

また、その他のデータについてはStandardScalerで標準化する。

CHASのデータのみone-hot化
CHASの列を除いたデータをStandardScalerで標準化
上記2つのデータをjoin()で結合

df_chas_encoded = pd.get_dummies(df['CHAS'], prefix='CHAS')
df_wo_chas = df.drop('CHAS', axis=1)
df_wo_chas_scaled = pd.DataFrame(
    StandardScaler().fit_transform(df_wo_chas), columns=df_wo_chas.columns)
df_preprocessed = df_wo_chas_scaled.join(df_chas_encoded)

df_chas_encoded = pd.get_dummies(df['CHAS'], prefix='CHAS')

df_wo_chas = df.drop('CHAS', axis=1)

df_wo_chas_scaled = pd.DataFrame(

StandardScaler().fit_transform(df_wo_chas), columns=df_wo_chas.columns)

df_preprocessed = df_wo_chas_scaled.join(df_chas_encoded)

可視化

2次元

ここではまず、2次元可視化の結果を確認する。

クラス分類の場合は2次元で2つの主成分を確認できるが、回帰データの場合はターゲットの量を確認する必要があるため、グラフの軸を1つ消費する。このため、2次元による表現では1つの主成分による説明性を確認することになる。

各点の色や大きさをターゲットの値によって変化させ、2つの軸を2つの主成分に割り当てる方法も考えられるが、直感的にとらえにくくなる。

この結果を見る限り、あまり美しい結果とはなっていない。データを俯瞰した際、各特徴量であまりいい説明ができなかったが、その中でもある程度関係がみられたMDEVやLSTATとの相関と変わらないくらい。

3次元

そこで3次元の可視化にして、2つの主成分による説明性を確認する。

これでもあまりいい結果にならない。ただしグラフを見ると、大きく2つの塊に分かれているように見える。ターゲットである住居価格とは別に、特徴量の組み合わせに隠れている、性質の違うグループがあるのかもしれない。

主成分と寄与率

2つの主成分と寄与率について表示させてみる。

Components:
     feature    comp_0    comp_1
0       CRIM  0.251012  0.399530
1         ZN -0.256281  0.436197
2      INDUS  0.346630 -0.109264
3        NOX  0.342782 -0.169987
4         RM -0.189333  0.063747
5        AGE  0.313601 -0.318114
6        DIS -0.321462  0.331591
7        RAD  0.319816  0.381156
8        TAX  0.338513  0.318517
9    PTRATIO  0.205059  0.182159
10         B -0.203023 -0.333020
11     LSTAT  0.309817 -0.027564
12  CHAS_0.0 -0.001091  0.035239
13  CHAS_1.0  0.001091 -0.035239

Explained :[0.50514047 0.1109301 ]

Components:

feature comp_0 comp_1

0 CRIM 0.251012 0.399530

1 ZN -0.256281 0.436197

2 INDUS 0.346630 -0.109264

3 NOX 0.342782 -0.169987

4 RM -0.189333 0.063747

5 AGE 0.313601 -0.318114

6 DIS -0.321462 0.331591

7 RAD 0.319816 0.381156

8 TAX 0.338513 0.318517

9 PTRATIO 0.205059 0.182159

10 B -0.203023 -0.333020

11 LSTAT 0.309817 -0.027564

12 CHAS_0.0 -0.001091 0.035239

13 CHAS_1.0 0.001091 -0.035239

Explained :[0.50514047 0.1109301 ]

寄与率は第1主成分が50%程度で低いため高い相関が出ないといえるかもしれない。だが、Breast cancerデータセットのクラス分類では第1主成分の寄与率が40%台だが、明確なクラス分類ができていた。やはり回帰系の問題にはPCAは不向きなのかもしれない。

主成分の要素について、先の散布図が第1主成分と負の相関があることから、第1主成分の各特徴量は価格低下に寄与するものはプラス、価格上昇に寄与するものはマイナスとなるはずである。

たとえばZNやRMがマイナスなのは頷けるが、DISがマイナスなのは微妙。TAXやPRATIOがプラスなのも逆のような気がする。

先にも書いたが、Boston housing pricesデータセットで取りそろえられた特徴量は、住居の価格以外の何かを特徴づける傾向が強いのかもしれない。

PCA – Breast cancerデータセット

2020-11-20 / tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をBreast cancerデータセットに適用して、その挙動を確認する。

30個の特徴量（全て連続量）を持つ569個の腫瘍データについて、悪性(marignant)／良性(benign)がターゲットとして与えられている。PCAによって特徴量のみの分析で、少ない主成分によってある程度明確な分離が可能なことが示される。

手順

以下の手順・コードで計算した。

パッケージをインポート
Breast cancerデータセットを準備
データセットをスケーリング
- StandardScalerで特徴量データを標準化している
PCAモデルのインスタンスを生成
- 引数n_components=3で3つの主成分まで計算させている
fit()メソッドによって、モデルにデータを学習させる
成分やその寄与率を確認
- 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
transform()メソッドによって、主成分に沿ってデータを変換
3つの主成分について3次元可視化
2つの主成分について2次元可視化

主成分と寄与率

以下に主成分と寄与率を計算するまでのコードを示す。

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D

ds = load_breast_cancer()
X_scaled = StandardScaler().fit_transform(ds.data)
df = pd.DataFrame(X_scaled, columns=ds.feature_names)

pca = PCA(n_components=3)
pca.fit(df)

print("Components:\n{}".format(pca.components_))
# Components:
# [[ 0.21890244  0.10372458  0.22753729  0.22099499  0.14258969  0.23928535
#    0.25840048  0.26085376  0.13816696  0.06436335  0.20597878  0.01742803
#    0.21132592  0.20286964  0.01453145  0.17039345  0.15358979  0.1834174
#    0.04249842  0.10256832  0.22799663  0.10446933  0.23663968  0.22487053
#    0.12795256  0.21009588  0.22876753  0.25088597  0.12290456  0.13178394]
#  [-0.23385714 -0.0597061  -0.21518137 -0.23107672  0.18611299  0.15189161
#    0.06016536 -0.03476749  0.19034877  0.36657548 -0.10555215  0.0899797
#   -0.08945723 -0.15229263  0.20443047  0.23271588  0.19720726  0.13032158
#    0.18384799  0.28009201 -0.21986638 -0.0454673  -0.19987843 -0.21935186
#    0.17230435  0.14359318  0.09796412 -0.00825721  0.14188335  0.27533948]
#  [-0.00853135  0.06454967 -0.00931432  0.02869944 -0.10429256 -0.07409161
#    0.00273383 -0.0255634  -0.0402399  -0.02257393  0.26848142  0.37463394
#    0.26664551  0.21600645  0.30883931  0.15477941  0.17646341  0.22465797
#    0.28858416  0.21150348 -0.04750699 -0.0422979  -0.04854648 -0.0119023
#   -0.25979771 -0.23607553 -0.17305727 -0.17034366 -0.27131257 -0.23279102]]

print("Explained :{}".format(pca.explained_variance_ratio_))
# Explained :[0.44272026 0.18971182 0.09393163]

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.preprocessing import StandardScaler

from sklearn.decomposition import PCA

from mpl_toolkits.mplot3d import Axes3D

ds = load_breast_cancer()

X_scaled = StandardScaler().fit_transform(ds.data)

df = pd.DataFrame(X_scaled, columns=ds.feature_names)

pca = PCA(n_components=3)

pca.fit(df)

print("Components:\n{}".format(pca.components_))

# Components:

# [[ 0.21890244 0.10372458 0.22753729 0.22099499 0.14258969 0.23928535

# 0.25840048 0.26085376 0.13816696 0.06436335 0.20597878 0.01742803

# 0.21132592 0.20286964 0.01453145 0.17039345 0.15358979 0.1834174

# 0.04249842 0.10256832 0.22799663 0.10446933 0.23663968 0.22487053

# 0.12795256 0.21009588 0.22876753 0.25088597 0.12290456 0.13178394]

# [-0.23385714 -0.0597061 -0.21518137 -0.23107672 0.18611299 0.15189161

# 0.06016536 -0.03476749 0.19034877 0.36657548 -0.10555215 0.0899797

# -0.08945723 -0.15229263 0.20443047 0.23271588 0.19720726 0.13032158

# 0.18384799 0.28009201 -0.21986638 -0.0454673 -0.19987843 -0.21935186

# 0.17230435 0.14359318 0.09796412 -0.00825721 0.14188335 0.27533948]

# [-0.00853135 0.06454967 -0.00931432 0.02869944 -0.10429256 -0.07409161

# 0.00273383 -0.0255634 -0.0402399 -0.02257393 0.26848142 0.37463394

# 0.26664551 0.21600645 0.30883931 0.15477941 0.17646341 0.22465797

# 0.28858416 0.21150348 -0.04750699 -0.0422979 -0.04854648 -0.0119023

# -0.25979771 -0.23607553 -0.17305727 -0.17034366 -0.27131257 -0.23279102]]

print("Explained :{}".format(pca.explained_variance_ratio_))

# Explained :[0.44272026 0.18971182 0.09393163]

寄与率は第1主成分が44%、第2主成分が19%、第3主成分が9%。第3成分まで3/4の情報を説明していることになる。

また、第1主成分は全ての特徴量がプラス方向で寄与している。

主成分をヒートマップで視覚化してみると、各主成分の符号や大きさが直感的に把握しやすくなるが、第2～第3主成分がmeanとworst系の特徴量が小さい方が影響が大きい点、3つの主成分についてerrorが大きいほど影響が大きい点など、意味づけは難しい。

plt.matshow(pca.components_, cmap='seismic')
plt.yticks([0, 1, 2], ["Component-1", "Component-2", "Comoponent-3"])
plt.colorbar()
plt.xticks(range(len(ds.feature_names)),
    ds.feature_names, rotation=60, ha='left')
plt.xlabel("Feature")
plt.ylabel("Principal components")

plt.show()

plt.matshow(pca.components_, cmap='seismic')

plt.yticks([0, 1, 2], ["Component-1", "Component-2", "Comoponent-3"])

plt.colorbar()

plt.xticks(range(len(ds.feature_names)),

ds.feature_names, rotation=60, ha='left')

plt.xlabel("Feature")

plt.ylabel("Principal components")

plt.show()

可視化

3次元

3つの主成分について3次元で可視化してみると、悪性／良性がかなりはっきりと分離されている。

2次元

2つの主成分のみでも、悪性／良性がよく区分されている。

まとめ

Irisデータの場合と同じく、特徴量分析のみでクラスの別がよくあぶりだされている。

PCA – Irisデータセット

2020-11-20 / tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をIrisデータに適用して、その挙動を確認する。

クラス分類のターゲットを用いていないにもかかわらず、少ない主成分でクラスがかなり明確に分類されることがわかる。

計算の手順

以下の手順・コードで計算した。

必要なパッケージをインポート
Irisデータセットを準備
データセットをスケーリング
- StandardScalerで特徴量データを標準化している
PCAモデルのインスタンスを生成
- 引数n_componentsを指定せず、4つの特徴量全てを計算
モデルにデータを学習させる
- fit()メソッドのみでよいが、後のグラフ化のためにfit_transform()メソッドを実行
- X_transに主成分によって変換したデータを格納
主成分やその寄与率を確認
- 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
3つの主成分について3次元可視化
2つの主成分について2次元可視化

主成分と寄与率

以下に、主成分と寄与率を計算するまでのコードを示す。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D

iris_data = load_iris()

X = iris_data['data']
y = iris_data['target']
feature_names = iris_data['feature_names']
target_names = iris_data['target_names']

X_scaled = StandardScaler().fit_transform(X)

pca = PCA()
X_trans = pca.fit_transform(X_scaled)

print(pd.DataFrame(pca.components_, columns=feature_names))
#    sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
# 0           0.521066         -0.269347           0.580413          0.564857
# 1           0.377418          0.923296           0.024492          0.066942
# 2          -0.719566          0.244382           0.142126          0.634273
# 3          -0.261286          0.123510           0.801449         -0.523597

print(pca.explained_variance_ratio_)
# [0.72962445 0.22850762 0.03668922 0.00517871]

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

from sklearn.preprocessing import StandardScaler

from sklearn.decomposition import PCA

from mpl_toolkits.mplot3d import Axes3D

iris_data = load_iris()

X = iris_data['data']

y = iris_data['target']

feature_names = iris_data['feature_names']

target_names = iris_data['target_names']

X_scaled = StandardScaler().fit_transform(X)

pca = PCA()

X_trans = pca.fit_transform(X_scaled)

print(pd.DataFrame(pca.components_, columns=feature_names))

# sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)

# 0 0.521066 -0.269347 0.580413 0.564857

# 1 0.377418 0.923296 0.024492 0.066942

# 2 -0.719566 0.244382 0.142126 0.634273

# 3 -0.261286 0.123510 0.801449 -0.523597

print(pca.explained_variance_ratio_)

# [0.72962445 0.22850762 0.03668922 0.00517871]

寄与率の方を見てみると、第1主成分で約73%、第2主成分で23 %と、2つの主成分で特徴をほぼ説明しきっている（第3、第4主成分の寄与はほとんど無視できる）。

第1主成分の各要素の符号を見てみる。萼の長さ、花弁の長さと幅は同程度でプラス方向に効いていて、萼の幅はマイナス方向の効果を持っている。このことから、萼の細長さと花弁の全体的な大きさによって、アヤメの花が特徴づけられていると考えられる。また第2主成分は、萼の幅で殆ど特徴が決まっている。

可視化

3次元

4つの主成分のうち3つについて3次元で可視化してみると、3つのアヤメの種類がかなりきれいに分離されているのがわかる。

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))

X0 = X_trans[y==0]
X1 = X_trans[y==1]
X2 = X_trans[y==2]
ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2])
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2])
ax.scatter(X2[:, 0], X2[:, 1], X2[:, 2])

ax.set_xlabel("Component-1")
ax.set_ylabel("Component-2")
ax.set_zlabel("Component-3")

plt.show()

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))

X0 = X_trans[y==0]

X1 = X_trans[y==1]

X2 = X_trans[y==2]

ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2])

ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2])

ax.scatter(X2[:, 0], X2[:, 1], X2[:, 2])

ax.set_xlabel("Component-1")

ax.set_ylabel("Component-2")

ax.set_zlabel("Component-3")

plt.show()

2次元

第2主成分まででほとんどの特徴を説明できそうなので、2次元の散布図で表示してみる。

実際、2つの主成分だけでかなりきれいに3つのクラスが分かれている。少し重なっている部分があるが、先の主成分を3つの3次元グラフで傾きを調整すると、より明確にクラスが分けられる。

pca = PCA(n_components=2)
X_trans = pca.fit_transform(X_scaled)

print(pd.DataFrame(pca.components_, columns=feature_names))
print(pca.explained_variance_ratio_)

fig, ax = plt.subplots()

X0 = X_trans[y==0]
X1 = X_trans[y==1]
X2 = X_trans[y==2]
ax.scatter(X0[:, 0], X0[:, 1])
ax.scatter(X1[:, 0], X1[:, 1])
ax.scatter(X2[:, 0], X2[:, 1])

ax.set_xlabel("Component-1")
ax.set_ylabel("Component-2")

plt.show()

pca = PCA(n_components=2)

X_trans = pca.fit_transform(X_scaled)

print(pd.DataFrame(pca.components_, columns=feature_names))

print(pca.explained_variance_ratio_)

fig, ax = plt.subplots()

X0 = X_trans[y==0]

X1 = X_trans[y==1]

X2 = X_trans[y==2]

ax.scatter(X0[:, 0], X0[:, 1])

ax.scatter(X1[:, 0], X1[:, 1])

ax.scatter(X2[:, 0], X2[:, 1])

ax.set_xlabel("Component-1")

ax.set_ylabel("Component-2")

plt.show()

なお今回の計算では、PCAのモデルインスタンス生成時にn_components=2としている。その結果は以下の通りで、1つ前の結果と同じ値になっている。

   sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
0           0.521066         -0.269347           0.580413          0.564857
1           0.377418          0.923296           0.024492          0.066942
[0.72962445 0.22850762]

sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)

0 0.521066 -0.269347 0.580413 0.564857

1 0.377418 0.923296 0.024492 0.066942

[0.72962445 0.22850762]

主成分分析の特徴

IrisデータセットへのPCAの適用結果から、以下のようにまとめられる。

主成分分析の計算において、ターゲットのクラス分類は全く用いていない（特徴量データのみを用いている）
ターゲットのクラス分類は、散布図を描くときの色分けにのみ利用している
それにも関わらず、散布図において3つのクラスがかなりきれいに分離されている
特徴量の線形和に沿った分散の最大化、という問題設定で、その背後にあるアヤメの種類がうまく分類されている

主成分分析の定式化

2020-11-20 / tau / コメントする

概要

主成分分析では、複数の特徴量を持つデータセットから、そのデータセットの特徴を最もよく表す特徴量軸を発見していく。

ここで「特徴を最もよく表す」ことを数学的に「最も分散が大きくなる」と定義する。そして、分散が最も大きくなるような方向を探すことを目的とする。

ある軸に沿った分散が大きくなるということは、その軸に沿った性質のバリエーションが多いことになる。逆に分散が小さい場合は、その性質を表す数量によっては各データの特徴の違いが判別しにくい。

主成分分析では、分散が最大となるような軸の方向を発見することが目的となる。この軸は元の特徴量の線形和で表現されるもので、各特徴量の係数は、それぞれの特徴量の寄与を表す。

(1) $\begin{align*} \boldsymbol{v} &= a_1 \boldsymbol{x}_1 + \ldosts + a_m \boldsymbol{x_m} \\ &= a_1 \left( \begin{array}{c} \x_1 \\ 0 \\ \vdots \\ 0 \end{array} \right) + \cdots + a_m \left( \begin{array}{c} 0 \\ \vdots \\ 0 \\ x_m \end{array} \right) \\ v &= | \boldsymbol{v} | = a_1 x_1 + \cdots + a_m x_m \end{align*}$

以後、複数の特徴量を持つデータを、特徴量を成分とするベクトルでx表し、多数のベクトルデータx_iがデータセットを構成しているとする。

最大化すべき分散の導出

多数のデータの中のデータiが空間内の点に対応し、その位置ベクトルをx_iであるとする。このx_iの成分が特徴量に対応する。長さが1のあるベクトルdが与えられたとき、x_iのdへの射影の長さは以下のように計算される。

(2) $\begin{align*} x_{i | \boldsymbol{d}} = {\boldsymbol{x}_i}^T \boldsymbol{d} = \boldsymbol{d}^T \boldsymbol{x}_i \quad (| \boldsymbol{d} | = 1) \end{align*}$

たとえば特徴量が2つなら、2次元で以下のような計算になる。

(3) $\begin{align*} \boldsymbol{x}_i = \left( \begin{array}{C} x_{i1} \\ x_{i2} \end{array} \right) , \quad \boldsymbol{d} = \left( \begin{array}{C} d_1 \\ d_2 \end{array} \right) \end{align*}$

(4) $\begin{align*} x_{i | \boldsymbol{d}} = ( d_1 , d_2 ) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) = ( d_1 x_{i1} + d_2 x_{i2} ) \end{align*}$

n個のデータ(i = 1～n)について、射影の平均は以下のように計算される。これは全データのベクトルdの方向に沿った値の平均となる。

(5) $\begin{align*} E( x_{i | \boldsymbol{d}} ) = E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) = \boldsymbol{d}^T E \left( \boldsymbol{x}_i \right) = \boldsymbol{d}^T \boldsymbol{\mu}_i \end{align*}$

これも2次元の場合で確認すると以下の通り。

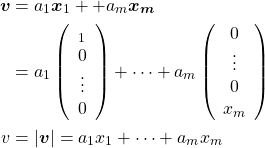
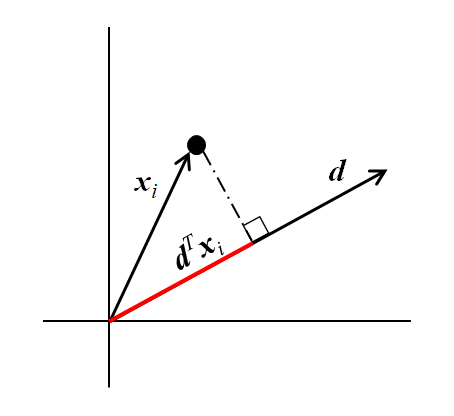
(6) $\begin{align*} E(x_{i | \boldsymbol{d}} ) &= E\left[ (d1, d2) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) \right] = (d_1, d_2) \left( \begin{array}{c} E(x_{i1}) \\ E(x_{i2}) \end{array} \right) \\ &= (d_1, d_2) \left( \begin{array}{c} \mu_{i1} \\ \mu_{i2} \end{aray} \right) \end{align*}$

式(5)を使ってベクトルdの方向に沿ったデータの分散を計算する。

(7) $\begin{align*} V( x_{i | \boldsymbol{d}} ) &= V \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \\ &= E \left[ \left( \boldsymbol{d}^T \boldsymbol{x}_i - E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \right)^2 \right] \\ &= E \left[ \left( {\boldsymbol{d}}^T \left( \boldsymbol{x}_i - E(\boldsymbol{x}_i) \right) \right)^2 \right] \\ &= E \left[ {\boldsymbol{d}}^T (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \boldsymbol{d} \right] \\ &= \boldsymbol{d}^T E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \boldsymbol{d} \\ &= \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \end{align*}$

中央の平均の項が共分散行列Σとなっていることに留意。これより、あるベクトルが与えられたとき、その方向に沿った全データの成分の分散が、そのベクトルと元のデータの共分散行列を使って求めることができる。

こちらを2次元で確認すると以下の通り。

(8) $\begin{align*} &E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \\ &= E \left[ \left( \begin{array}{c} x_{i1} - \mu_1 \\ x_{i2} - \mu_2 \end{array} \right) (x_{i1} - \mu_1, x_{i2} - \mu_2) \right] \\ &= \left[ \begin{array}{cc} (x_{i1} - \mu_1)^2 & (x_{i1} - \mu_1)(x_{i2} - \mu_2) \\ (x_{i2} - \mu_2)(x_{i1} - \mu_1) & (x_{i2} - \mu_2)^2 \end{array} \right] \end{align*}$

分散の最大化

式(8)で計算された分散が最大となるようにベクトルdの方向を決定する。このとき、dの大きさが1であるという制約条件があるため、問題は制約条件付きの最大化問題となる。

(9) $\begin{gather*} {\rm max} \quad \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \quad \rm{s.t.} \; | \boldsymbol{d} | = 1 \end{gather*}$

これをLagrangeの未定乗数法で解いていく。。

(10) $\begin{gather*} L( \boldsymbol{d}, \lambda ) = \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} - \lambda (|\boldsymbol{d}|^2 - 1) = 0 \\ \frac{\partial L}{\partial d_i} = 0 \quad ( {\rm for \; all} \; i ) \end{gather*}$

Lagrange関数の第1項については、

(11) $\begin{align*} \boldsymbol{d}^T \boldsymbol{\Sigma} &= \begin{array}{ccc} ( & d_1 V_1 + \cdots + d_n C_{n1} & , \\ & \vdots & ,\\ & d_1 C_{1j} + \cdots + d_n C_{n, j} & , \\ & \vdots & ,\\ & d_1 C_{1n} + \cdots + d_n V_n & ) \end{array} \end{align*}$

より、以下のような長い式になる。

(12) $\begin{align*} \boldsymbol{d}^T \boldsymbol{\Sigma d} &= \begin{array}{c} {d_1}^2 V_1 + \cdots + d_j d_1 C_{j1} + \cdots + d_n d_1 C_{n1} + \\ \vdots \\ d_1 d_j C_{1j} + \cdots + {d_j}^2 V_j + \cdots + d_n d_j C_{nj} + \\ \vdots \\ d_1 d_n C_{1n} + \cdots + d_j d_n C_{jn} + \cdots + {d_n}^2 V_n \end{array} \end{align*}$

また第2項の括弧の中については以下のようになる。

(13) $\begin{align*} | \boldsymbol{d} |^2 - 1 = ( {d_1}^2 + \cdots + {d_j}^2 + \cdots + {d_n}^2 ) -1 \end{align*}$

これらを前提に、Lをd_jで微分すると以下のようになる。

(14) $\begin{align*} 2 d_1 C_{1j} + \cdots + 2 d_j V_{j} + \cdots 2 d_n C_{2j} - 2 \lambda d_j = 0 \end{align*}$

全てのd_jについて考慮した連立方程式を行列形式で表すと以下のようになる。

(15) $\begin{gather*} \boldsymbol{\Sigma d} = \lambda \boldsymbol{d} \\ | \boldsymbol{d} | = 1 \end{gather*}$

1つ目の式は共分散行列に関する固有値問題の式で、d_i (i=1～n)とλのn+1個の変数に対してn個の式となる。これに先ほど脇に置いていたdの大きさに関する制約式を加えて式の数もn+1個となり、dとλが求められる。

特徴量が2つの場合

特徴量が2つの場合を考え、以下のように記号を定義する。

(16) $\begin{align*} \boldsymbol{\Sigma} = \left( \begin{array}{cc} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{array} \right) , \quad \boldsymbol{d} = \left( \begin{array}{c} d_1 & d_2 \end{array} \right) \end{align*}$

このとき、分散を最大化する方向の単位ベクトルdを求める方程式は以下のようになる。

(17) $\begin{equation*} \left\{ \begin{array}{l} \left( \begin{array}{cc} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{array} \right) \left( \begin{array}{c} d_1 & d_2 \end{array} \right) = \lambda \left( \begin{array}{c} d_1 & d_2 \end{array} \right) \\ {d_1}^2 + {d_2}^2 = 1 \end{array} \right. \end{equation*}$

1つ目の式を解くと、

(18) $\begin{equation*} \left\{ \begin{array}{l} \sigma_{11} d_1 + \sigma_{12} d_2 = \lambda d_1 \\ \sigma_{21} d_1 + \sigma_{22} d_2 = \lambda d_2 \end{array} \rhight. \end{equation*}$

この方程式は不定なのでd₁、d₂それぞれは求められないが、μ = d₂/d₁は計算できる。これは固有ベクトルの方向が定まる。具体的には下記の通り。

(19) $\begin{gather*} \left\{ \begin{array}{l} \sigma_{11} + \sigma_{12} \mu = \lambda \\ \sigma_{21} + \sigma_{22} \mu = \lambda \mu \end{array} \right. \\ \lambda = \sigma_{11} + \sigma_{12} \mu = \frac{\sigma_{21}}{\mu} + \sigma_{22} \\ \sigma_{12} \mu^2 + ( \sigma_{11} - \sigma_{22} ) \mu - \sigma_{21} = 0 \end{gather*}$

これを解いてベクトルdの方向が定まる。これに制約条件|d|² ＝１を加味することで、大きさ1の単位ベクトルとしてdが決定される。

この解き方は最大化問題ではないので、連立方程式から2つの固有ベクトルと固有値が求まる。

第2主成分以降

一般的な固有値問題では、元の変数と同じ数の固有ベクトルと固有値のセットが求まるが、最大化問題として解いた場合には主成分が1つだけ求まる。

scikit-learnのPCAインスタンス生成時にn_componentsで主成分の数に制約をかけることができるが、このことから、PCA.fit()の実行時には連立方程式を解いているのではなく、最大化問題で1つずつ主成分を計算しているのではないかと思われる。

第2主成分以降の計算についての紹介はあまり見られないが、以下の手順と考えらえれる。

各データについて、第1主成分の方向への射影を計算
その射影の符号を逆にしたベクトルを各データに加える
これで第1主成分に沿ったばらつきが全てゼロになるので、残りの成分の中で最大となるベクトルの方向を計算し、第2主成分とする
以上を繰り返し、順次最大主成分沿いの情報を消しながら、各主成分を計算

主成分の意味

主成分の意味の一つに、元のデータを構成する成分という捉え方がある。

たとえば特徴量の数がnである元データXがあり、主成分の数をm(<= n)でモデルを構築するとする。scikit-learnでPCAのインスタンスを生成するのにn_components=mと指定し、fit(X)を実行すると、m個の主成分が生成される。この主成分は共分散行列に対する固有ベクトルであり、要素数n個（特徴量数に等しい）の1次元配列がm行（主成分の数に等しい）並んだ2次元配列として、PCAインスタンスのプロパティーcomponents_に保存される。

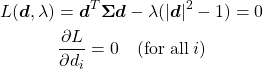
(20) $\begin{equation*} \tt{components\_} = \left[ \begin{array}{ccc} (p_{0, 0} & \cdots & p_{0, n-1} ) \\ & \vdots &\\ (p_{m-1, 0} & \cdots & p_{m-1, n-1}) \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{p}_0 \\ \vdots \\ \boldsymbol{p}_m \end{array} \right] \end{equation*}$

元のデータは、各主成分（固有ベクトル）の重み付き和として表現される。

(21) $\begin{equation*} \boldsymbol{x} = (x_0, ..., x_n) = a_0 \boldsymbol{p}_0 + a_1 \boldsymbol{p}_1 + a_2 \boldsymbol{p}_2 + \cdots \end{equation*}$

この様子を2次元で示したのが以下の図で、直行する2つの主成分から元データの１つxが定まる。

xの主成分1、2の方向の大きさはxの各主成分に対する射影で、それらの長さはxと各主成分の内積で得られる。

(22) $\begin{equation*} \boldsymbol{x} = (x_0, ..., x_n) = ( \boldsymbol{x} \cdot \boldsymbol{p}_0 ) \boldsymbol{p}_0 + ( \boldsymbol{x} \cdot \boldsymbol{p}_1 ) \boldsymbol{p}_1 + ( \boldsymbol{x} \cdot \boldsymbol{p}_2 ) \boldsymbol{p}_2 + \cdots \end{equation*}$

感度＝陽性的中率の特性

2020-11-16 / tau / コメントする

概要

機械学習のモデルの性能や感染症検査の確からしさを検証する際、陽性的中率（適合度）や陰性的中率を確認すべきだが、これらの値が、そもそものデータの特性やモデル／検査の性能によってどのように変化するかを確認する。

具体的には、注目事象の率と真陽性率（感度）・真陰性率（特異度）を変化させたときの、陽性的中率・陰性的中率の変化を見る。

これらの値の意味や計算方法については、Confusing matrixを参照。

その結果から、以下のようなことがわかった。

予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
特異度を向上させることで適合度は大きく向上する
ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

2020年現在、世界的に大きな影響を及ぼしているCOVID-19（新型コロナウィルス）感染症のPCR検査では、一般に感度が70％程度、特異度が90％以上、陽性的中率が数%程度という値が多い。感度が7割程度というのは少し低く、陽性的中率がそもそも小さすぎるという気がしていたが、上記のことと符合することがわかった。

指標

以下の指標を、目的として計算する指標とする。

PPV(Positive Predicted Value)：陽性的中率、適合度、Precision
NPV(Negative Predicted Value)：陰性的中率

これらの指標を計算するために用いる指標は以下の通り。

TR(Target Rate)：注目事象の全体比率（ターゲット比率）
TPR(True Positive Rate)：真陽性率、感度(Sencitivity)
TNR(True Negative Rate)：真陰性率、特異度(Specificity)

例えば感染症の例で言うと、有病率(TR)、検査の感度(TPR)、特異度(TNR)がわかっているときに、陽性的中率(PPV)、陰性的中率(NPV)を求めることに相当する。

PPV・NPVの計算式の導出

元データの構成

まず、confusing matrixを以下のように表現する。これは、データ数で表現されたテーブルの各要素を全データ数で割った率で表すことに相当する。

$\begin{align*} \begin{array}{cc|cc|c} & & \mathrm{Prediction}\\ & & \mathrm{Positive} & \mathrm{Negative} & \mathrm{Sum} \\ \hline \mathrm{Fact} & \mathrm{Positive} & tp & fn & r_1 \\ & \mathrm{Negative} & fp & tn & r_2 \\ \hline & \mathrm{Sum}& c_1 & c_2 & 1 \end{array} \end{align}$

PPV・NPVの計算式

まず、事実(Fact)がpositiveである率がr₁に相当し、これはTR (target rate)に等しい。このTRと率TPRを使って、Positiveの行のtp(true positive)とfn (false negative)の率を計算。

(1) $\begin{align*} r_1 &= TR \\ tp &= r_1 \cdot TPR = TR \cdot TPR \\ fn &= r_1 \cdot (1 - TPR) = TR (1 - TPR) \end{align*}$

2行目の合計r₂については、行和の合計が1になることから以下のように計算される。

(2) $\begin{align*} r_2 &= 1 - r_1 = 1 - TR \end{align*}$

このr₂と率TNRからNegativeの行のtn(true negative)とfp (false positive)を計算。

(3) $\begin{align*} tn &= r_2 \cdot TNR = (1 - TR) TNR \\ fp &= r_2 (1 - TNR) = (1 - TR) (1 - TNR) \end{align*}$

tpとfpからc₁を、tnとfnからc₂を計算。

(4) $\begin{align*} c_1 &= tp + fp = TR \cdot TPR + (1 - TR) (1 - TNR) \\ c_2 &= tn + fn = (1 - TR) TNR + TR (1 - TPR) \end{align*}$

PPV（陽性的中率、感度）はc₁に対するtpの率で計算される。以下の式は分数の分数で若干ややこしいが、3つの指標が1回ずつ現れ、整った形になる。

(5) $\begin{align*} PPV &= \frac{tp}{c_1} = \frac{TR \cdot TPR}{TR \cdot TPR + (1 - TR) (1 - TNR) } \\ &= \frac{1}{1 + \left(\dfrac{1}{TR} - 1 \right) \dfrac{1 - TNR}{TPR}} \end{align*}$

NPV（陰性的中率、特異度）はc₂に対するtnの率で計算される。以下の式とPPVの式を比べると、はTRの分数項ついて逆数であり、TPRとTNRが入れ替わっていて、PPVとNPVで対称性がある。

(6) $\begin{align*} NPV &= \frac{tn}{c_2} = \frac{(1 - TR) TNR}{(1 - TR) TNR + TR (1 - TPR)}\\ &= \frac{1}{1 + \dfrac{TR}{1 - TR} \dfrac{1 - TPR}{TNR}} \end{align*}$

パラメーターに応じたPPV・NPVの変化

PPV

上記の結果を用いて、ターゲット比率、真陽性率（感度）、真陰性率（特異度）の様々な値に対するPPV（陽性的中率）、NPV（陰性的中率の変化を観察する。

まず、ターゲット比率が1に近い（ほとんどがターゲットとなるような）状態から、ターゲットが0に近いような（ターゲットとなるデータがほとんどないような）状態の間で、PPVがどのように変化するか確認してみる。

TPR（感度）の値によって曲線の形に若干の変化はあるがあまり大きくは変わらず、むしろTNR（特異度）の値による曲線の形状の変化が大きい。ここでTRが0.1～0と小さい範囲のところを見てみる。

やはり感度の影響はあまり大きくないようである。TNRを大きくするにしたがって曲線の形状は大きく変化し、ターゲット比率が小さいところでの適合度が向上するが、ターゲット比率が0に近いところではPPVがかなり小さくなる。

次に、TPRを変化させたときの曲線の違いが分かるように、表示させる変数を入れ替えてみる。まずTRが1～0の全域。

やはり感度による曲線の変化は小さく、特異度の影響が大きい。以下のようにTRが0.1～0の範囲を拡大しても同様の傾向。

以上の結果から、以下のことが言える。

ターゲット比率が低くなるほどNPVは小さくなる（適合度が低くなり、予測／検査の信頼性が下がる）
予測モデルや検査のTPR（感度）を上げることによるPPVの向上効果はあまり大きくない（いたずらに感度を上げても顕著な効果はない）
TNR（特異度）の向上によって、適合度は大きく向上する
ターゲット比率がとても小さい場合、その率の現象に従って適合度は急激に低下する

さらにこれを一般的な表現でまとめると、

予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
特異度を向上させることで適合度は大きく向上する
ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

NPV

PPVと同様にNPVについても計算してみた。

まずいくつかのTPRに対して、TNRを変化させて曲線を描いたもの。PPVの場合と比べて形状が左右逆で、TNRを固定してTPRを変化させたときの図と同じ傾向。

次に、いくつかのTNRを固定してTPRを変化させたもの。これもPPVと形状、TPR、TNRの関係が逆になっている。

PPVとNPVの関係

PPVとNPVが同じTPR、TNRに対してどのように変化するか重ねてみる。

TPRとTNRを同程度とすることでターゲット比率0.5付近で双方が等しくなり、その値を高くすることで、より広い範囲でPPVが向上する。

シミュレーションによる挙動確認

これまでの結果は、confusion matrixの各要素にTR、TPRなどの比率を適用してPPV、NPVを計算した。この方法は、ある予測／判定が理論通りに再現された場合だが、実際にはターゲットとなる事象の割合も、予測がpositive/negativeになる割合も確率事象である。

そこで念のため、多数の二値(True/False)正解データをランダムに生成し、これに対してTPR、TNRの設定に従った答えを出す疑似的なモデルで「予測」する。その結果を整理したconfusion_matrixからPPVを計算したのが以下の図である。

その結果は計算式による場合と同じで、理論上の挙動と実世界で起こるであろう挙動が一致している。

処理内容は以下の通り。

与えられたTrue/Falseに対して、あらかじめ設定したTPR/TNRと一様乱数に従ってTrue/Falseを「予測」する疑似予測モデルを準備
TR=1～0の間で100個のデータについてPPVを計算する
- 1つのTRについて10万個の2値正解データを生成
- 正解データセットを疑似予測モデルに適用して予測データセットを得る
- 予測データセットからconfusion matrixを構成し、その要素からPPVを計算し、配列に格納
以上の結果をプロット

import numpy as np
import random as rnd
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix

def generate_data(target_rate=0.5, data_size=1000):
    y = np.empty(data_size, dtype=bool)
    for i in range(data_size):
        y[i] = rnd.random() < target_rate
    return y

class ImitationLearningModel:
    def __init__(self, tpr, tnr):
        self.tpr = tpr
        self.tnr = tnr

    def predict(self, y_fact):
        y_pred = np.empty(y_fact.size, dtype=bool)
        for i in range(y_fact.size):
            if y_fact[i]:
                y_pred[i] = rnd.random() < self.tpr
            else:
                y_pred[i] = rnd.random() > self.tnr
        return y_pred

fig, ax = plt.subplots()

tpr = 0.9
tnrs = [0.5, 0.7, 0.9, 0.99]

n_data = 100
trs = np.linspace(0, 1, n_data)
ppv = np.empty((len(tnrs), trs.size))

for j, tr in enumerate(trs):
    y_fact = generate_data(target_rate=tr, data_size=100000)
    for i, tnr in enumerate(tnrs):
        model = ImitationLearningModel(tpr, tnr)
        y_pred = model.predict(y_fact)
        cfmat = confusion_matrix(y_fact, y_pred, labels=[True, False])
        ppv[i, j] = cfmat[0, 0] / (cfmat[0, 0] + cfmat[1, 0])

for i, tnr in enumerate(tnrs):
    ax.plot(trs, ppv[i], label=tnr)

ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.invert_xaxis()
ax.set_xlabel("Target Rate")
ax.set_ylabel("PPV")
ax.legend()
ax.legend(title="TNR", loc='lower left')
ax.set_title("TPR={}".format(tpr))

plt.show()

import numpy as np

import random as rnd

import matplotlib.pyplot as plt

from sklearn.metrics import confusion_matrix

def generate_data(target_rate=0.5, data_size=1000):

y = np.empty(data_size, dtype=bool)

for i in range(data_size):

y[i] = rnd.random() < target_rate

return y

class ImitationLearningModel:

def __init__(self, tpr, tnr):

self.tpr = tpr

self.tnr = tnr

def predict(self, y_fact):

y_pred = np.empty(y_fact.size, dtype=bool)

for i in range(y_fact.size):

if y_fact[i]:

y_pred[i] = rnd.random() < self.tpr

else:

y_pred[i] = rnd.random() > self.tnr

return y_pred

fig, ax = plt.subplots()

tpr = 0.9

tnrs = [0.5, 0.7, 0.9, 0.99]

n_data = 100

trs = np.linspace(0, 1, n_data)

ppv = np.empty((len(tnrs), trs.size))

for j, tr in enumerate(trs):

y_fact = generate_data(target_rate=tr, data_size=100000)

for i, tnr in enumerate(tnrs):

model = ImitationLearningModel(tpr, tnr)

y_pred = model.predict(y_fact)

cfmat = confusion_matrix(y_fact, y_pred, labels=[True, False])

ppv[i, j] = cfmat[0, 0] / (cfmat[0, 0] + cfmat[1, 0])

for i, tnr in enumerate(tnrs):

ax.plot(trs, ppv[i], label=tnr)

ax.set_xlim(0, 1)

ax.set_ylim(0, 1)

ax.invert_xaxis()

ax.set_xlabel("Target Rate")

ax.set_ylabel("PPV")

ax.legend()

ax.legend(title="TNR", loc='lower left')

ax.set_title("TPR={}".format(tpr))

plt.show()

Confusion Matrix～混同行列

2020-11-12 / tau / コメントする

概要

精度が高いのに性能が悪い？

クラス分類の機械学習の結果、全体の精度のほか、注目しているクラスの分類性能などについて確認しておく必要がある。

たとえば製造部品の良／不良を判別するケースで不良品の確率が1/1000などとても小さい場合や、疾病の判定をするケースで罹患する率が1万人に1人と非常に低い場合を考えてみる。

求めているのは、僅かに発生する不良品を選りだすことや、稀に罹患している人を特定することだ。このとき、ターゲットでない（正常品や罹患していない）多数のクラスを正確に分類できれば全体の正解率は上がる。ところがその一方で、求めている事象（不良品や罹患者の）ターゲットの分類精度が低いと、正解率には影響しないが本来求めているターゲットの分類機能としては低くなる。

誤判定の度合い

このほか、疾病に罹患していると判定したのに実際には罹患していない場合や、罹患していないと判定したのに実は罹患している場合など、分類器の誤判定の度合いも重要だ。

間違ってターゲットを特定してもいいから漏れがないようにしたいのか、誤って特定するリスクを避けたいのか、それらをもちいるケースに応じて分類器の性能がどうあるべきかを検討する必要がある。

confusion matrixの活用

このような場合にもちいられるのがconfusion matrixである。それは機械学習において用いられるテーブルで、クラス分類のターゲットクラスと予測されたクラスを行と列にとり、各々がどのように一致しているか／異なっているかを示したものである。

その要素と行／列の合計から、予測モデルの性能を示す様々な指標を計算することができる。

Confusion matrixの構成

3クラス分類の例

Confusion matrixは以下のように構成される。

行（または列）に正解のクラス列を、（または行）に予測されたクラスの列を、同じ順番で並べる
各正解クラスに対して、予測されたクラスの数を入れていく

例えば画像認識で果物を判別する予測モデルを考え、りんご、梨、洋梨の3つのクラスを分類するものとする。このとき、ある予測を行った結果として得られたconfusion matrixの一例を示す。

行の側に正解（事実）、列の側に予測（判定）を置いているが、この定義は場合によって入れ替わる（Scikit-learnのライブラリーではこれと同じ配置だが、WikipediaのConfusion matrixの解説では逆になっている）。

		予測
		りんご	梨	洋梨	計
正解	りんご	80	15	5	100
	梨	27	70	3	100
	洋梨	2	3	95	100
	計	109	88	103	300

2クラス分類での一般化

左記の果物のconfusion matrixは3クラス分類の例だが、以下は2クラス分類で考えていく。様々な2クラス分類におけるconfusion matrixの共通した構成を一般化したのが以下の図である。2つのクラスのうち”Positive”と表現しているのが「特に捕捉したい／注目している事象」に分類されるもので、たとえば不良品や疾病の発見、成長企業の特定など。他方はそれ以外で、製造品が正常、被検者が罹患していないといった捕捉の対象としない事象に対応する。

Positiveな事象（注目している事象）について、英語では”relevant instances”などの表現が使われているが、relevantの意味には、直訳の「関連～」だけではなく「重要な」というニュアンスもあるようなので、ここでは「注目」という用語を使う。

まず表の左上と右下について。予測した事象と実際の事象が一致している場合で色が同じになっている。この場合は予測が正しいという意味でTrueとする。左上はPositive（注目事象）と予測してそれが正しいのでTrue Positive (TP)と呼ぶ。また右下はNegative（注目していない事象）と予測してそれが正しいのでTrue Negative (TN)と呼ぶ。

次に左下と右上について。今度は予測結果の色と事実の色が異なっている。この場合は予測が誤っているという意味でFalseとする。左下はPositiveと予測したが誤りなのでFalse Positive (FP)、一方右上は予測がNegativeだがそれが誤りなのでFalse Negative (FN)と呼ぶ。

True/FalseとPositive/Negativeの順番とテーブル上の位置がややこしいが、常に予測・判定結果から見てそれが事実に対して正しいか誤りかと考えて「正しい／誤った、Positive判定／Negative判定」と定義されている。

Positive/Negativeを疾病検査の陽性(potitive)／陰性(negative)にあてはめると、TP：真陽性、TN：真陰性、FP：偽陽性、FN：偽陰性とも呼ばれる。

2クラス分類の例

疾患検査

次に2クラス分類の実世界での例を見てみる。まず、よくある例として、ある疾患にかかっているかどうかを検査する例。この場合はまさしく予測が陽性(Positive)か陰性(Negative)かに相当する。FPならば罹患していない人が不要な治療・対応を受けることになり、FNならば罹患している人を見逃すことになる。

犯人特定

次に、カメラ画像や様々な証拠などから犯人を見つけ出すような問題。対象者が犯人であるという事象に注目して、これをpositiveな判定としている。FPの場合は無実の人の誤認逮捕に結びつき、FNならば犯人を取り逃がすことになる。

ヒット商品予測

これまでの2つは、どちらかと言えば注目事象がよくない影響を及ぼすものだったが、これがよい効果をもたらす例を考えてみる。以下の例は、開発しようとしている商品がヒットするかどうか、いろいろな情報に基づいて予測しようとするものである。FPならヒットしない商品に無駄な投資をすることになり、FNならばヒット商品の開発の機会を逃すことになる。

4つの象限の意味・結果

これらの例も見ながら、confusion matrixの4つの象限がどのような意味を持つか、以下のように整理してみる。

TP: 注目対象を正しく分類する。対処すべき事象が特定できる。
FP: 注目すべきでないものを誤って注目対象に分類してしまう。注目対象が好ましくない事象の場合はその対策に余計なコストがかかったり、場合によっては謂れのない差別などの対象となったりする。好ましい事象の場合は、無駄なコストをかけることになる。統計学で言う第2種の過誤にあたる。
TN: 注目対象以外のものを正しく分類する。注目対象を誤って見逃すことがなく、被害の拡大や機会損失を避けられる。
FN: 注目対象を誤って注目対象以外に分類してしまう。捕捉すべき望ましくないものを見逃して影響が拡大したり、望ましいものを見逃して利得を得る機会を逃したりする。統計学で言う第1種の過誤にあたる。

指標

Confusion matrixの4つの象限の値から、複数の指標が導かれる。それぞれの和名には、時々異なるものを指している例があるので、英語表現を基本にする。

全体に対する率

まず、4象限全体（すなわち全データ数）に対する率を考える。これらは注目事象か非注目事象かに関わらない、モデル全体の正確さを表す。

Accuracy（正解率・正確度）

予測結果が正しく注目対象と非注目対象を言い当てた率。4象限の対角要素の合計の、総計に対する率を計算する。様々な機械学習モデルのスコアとして計算される値に相当する。Accuracyは「（ばらつきはともかく）予測が真値をどれだけ（平均的に）言い当てているか」という意味。このAccuracyを「精度」と呼んでいる場合があるが、科学的な表現としては少しずれている。

(1) $\begin{equation*} \frac{TP + TN}{TP + FP + FN + TN} \end{equation*}$

Error Rate（不正解率）

Accuracyと逆で、予測結果が実際の注目・非注目対象から外れた率。4象限の非対角要素の合計の、総計に対する率として計算する。

(2) $\begin{equation*} \frac{FP + FN}{TP + FP + FN + TN} \end{equation*}$

正解・事実に対する率

表の横方向の、各行それぞれの合計に対する率。正解に対するモデルの正確さを表す。

Sensitivity/Recall/TPR
（感度・再現率・検出率・真陽性率）

正解が注目事象の場合に、モデルも注目事象と分類する率。疾病検査を例にすると、その検査が疾病をとらえる「感度・検出率」となる。TNR(True Positive Rate)：真陽性率については、この後も真～率、偽～率が出てくるが、これらはすべて行方向に対する（正解・事実に関する）予測・分類の正確さと定義される。”recall”のニュアンス（呼び戻す、想起するなど）は、この指標の意味に繋がりにくい。むしろ無理やり日本語にしたような「再現率」の方がまだ本来の意味に近いと感じられる。

(3) $\begin{equation*} TPR = \frac{TP}{TP + FN} \end{equation*}$

Specificity/TNR（特異度・真陰性率）

正解が注目していない事象の場合に、モデルがそれを間違いなく分類した率。疾病検査なら、罹患していない人の結果が陰性となる率。「特異度」という訳は”specific”～「特別な」というあたりから名付けたのかもしれないがセンスが悪い。むしろこれは問題ないものを問題ないと分類する率だから、「特異」ではないはずだ。せめてspecify～特定するで「特定率」くらいならまだしもか。TNRはTrue Negative Rate。

(4) $\begin{equation*} TNR = \frac{TN}{FP + TN} \end{equation*}$

FNR（偽陰性率）

FNR(False Negative Rate)はTPRの裏で、正解が注目事象なのにそうでないと分類してしまった率。罹患しているのに検査で陰性となる率に相当する。

(5) $\begin{equation*} FNR = 1 - TPR = \frac{FN}{TP + FN} \end{equation*}$

FPR（偽陽性率）

FPR(False Positive Rate)はTNRの裏で、正解が注目していない事象なのに注目事象だと判定してしまった率。罹患していないのに検査で陽性だと判定されてしまう率に相当する。

(6) $\begin{equation*} FPR = 1 - TNR = \frac{FP}{FP + TN} \end{equation*}$

予測・判定結果に対する率

表の縦方向、各列の合計に対する率。分類結果がどの程度信頼できるかを表す。日本のサイトではPPV、高々NPVまでしか紹介されていないが、英語版のWikipediaではすべて図入りで説明されている。

Precision/PPV（適合度・精度・陽性的中率）

Precision(適合度）はモデルが注目事象と予測した場合に、実際にそれが注目事象である率。疾病検査で陽性判定の場合に実際に罹患している率に相当する。なお、科学上の表現でのprecision（精度）は、本来ばらつきの小ささを意味する。PPVはPositive Predictive Value。

(7) $\begin{equation*} PPV = \frac{TP}{TP + FP} \end{equation*}$

NPV（陰性的中率）

NPV(Negative Predictive Value)はモデルが注目事象ではないと分類して、それがあたっている率。疾病検査で陰性の場合に罹患していない率に相当する。敢えて日本語で言うなら「適正排除率」くらいか。

(8) $\begin{equation*} NPV = \frac{TN}{FN + TN} \end{equation*}$

FDR（陽性誤り率？）

FDR(False Discovery Rate)はモデルが注目事象であると分類したのに、実際には非注目事象である率。英語表現の直訳なら「間違って発見する率」。検査で陽性判定だが罹患していない率に相当する。日本語の訳はないが、敢えて言うなら「過剰陽性判定率」とか「陽性失中率」くらいか。

(9) $\begin{equation*} FDR = 1 - PPV = \frac{FP}{TP + FP} \end{equation*}$

FOR（陰性誤り率？）

FOR(False Omission Rate)はモデルが注目事象でないと分類したのに注目事象である率。疾病検査で陰性判定だが、実は罹患している率に相当する。英語表現の直訳なら「間違って無視してしまう率」だが、日本語なら「逸失率」くらいか。

(10) $\begin{equation*} FOR = 1 - NPV = \frac{FN}{FN + TN} \end{equation*}$

指標間のトレードオフに対する疑問

一般に、Sensitivity（感度・検出率）とPrecision（適合度・陽性的中率）はトレードオフの関係にある、と述べられることが多い。これは単純な仕組みで感度を上げようとするときに、注目対象以外でも多めに陽性と判定すれば率は上がるが、その場合は陽性判定でも注目対象以外のものが多くなって適合率が下がる、ということから来ている。

ここが少しおかしい。感度を上げるにはTPを大きくしFNを小さくしなければならない。このとき適合度の側から見れば、TPが大きくなるなら適合度も上がるし、FNを小さくしたときにFPが大きくなるという相関関係がなければならない。

実際には、見落としを少なくしようとすれば、無関係なケースを陽性と判定する「濡れ衣(FP)」は増えるだろう。しかしこの「濡れ衣(FP)」は、いくら増えても感度には寄与しない。これは感度が上がっていないのに（不安なので）陽性が多めに出るようにしているに過ぎないと思われる。だとすると、このような方針は単に適合度を下げているだけで感度は向上せず、「トレードオフ」とは言えない。

その他の指標

F値

感度と適合度のトレードオフにには疑問があるが、そのバランスを保って双方向上させるというのは重要だ。このような指標がF値(F value)と呼ばれるもので、感度と適合度の調和平均として定義されている。

(11) $\begin{equation*} F = \left( \frac{1}{2} \left( \frac{1}{TPR} + \frac{1}{PPV} \right) \right) ^{-1} = \frac{2 TPR \cdot PPV}{TPR + PPV} \end{equation*}$

これを4象限のパラメーターを使って書き直してみる。

(12) $\begin{align*} F = \left( \frac{1}{2} \left( \frac{TP + FN}{TP} + \frac{TP + FP}{TP} \right) \right) ^{-1} &= \frac{2 TP^2}{2TP + FN + FP} \\ &= \frac{TP}{1 + \dfrac{FN + FP}{TP}} \end{align*}$

一般にF値は感度と適合率のトレードオフを想定して、双方を加味した指標とされているが、双方のバランスがとれた状態がF値を最大化するというわけでもなさそうだ。

用語について

“confusion”は、LONGMAN、Cambridgeなどの英英辞典を見ると、（不明瞭な状況、人や物事などの誤認による）混乱・混迷、（不快な状況下での）困惑というニュアンスで、confusion matrixを的確に表現できるものがない。英語サイトで「confusion matrixの語源は何か？」という問いかけがいくつか見られた。どうも心理学にその元があるようだが、その中で言及されている”classification matrix”の方が明快に思われる。実際、TP、FNなどのタームや指標の名称がかなりconfusingなことからみると、アメリカ流のジョークとも思えてしまう。

和名は「混同行列」とされているが、これも何と何を混同するのか不明瞭だ。”confusion”の的確な訳ではないので、何となくそれに近い言葉を一生懸命にあてたのかもしれない。それならいっそのこと、より的確な用語（判定行列とか）をあてればよかったのにと感じる。