カテゴリー: IT関係

pyplot.imshow – 画像表示

/ tau / コメントする

概要

matplotlib.pyplot.imshow()は画像表示用のメソッドで、表示対象として、画像ファイルや画像情報を格納した配列を指定する。

pyplotやsubplotで直接実行するほか、Axesオブジェクトのメソッドとしても実行できる。

ピクセルデータのレンジのデフォルト設定と与えるデータのレンジによって予期しない結果になることもあり、vmin、vmaxを明示的に指定した方がよい。

画像ファイルの表示

以下のコードは、JPEGファイルを読み込んで表示する。

ここではpyplot.subplotのメソッドとしてimshow()を実行している。画像が1つの場合、pyplot.imshow()でもよい。

1つは画像ファイルをそのまま引数にし、もう1つは画像ファイルを配列の形にしてから引数に渡している。画像の配列の形については後述。

配列の画像表示

基本形

imshow()は配列を引数にとることができる。

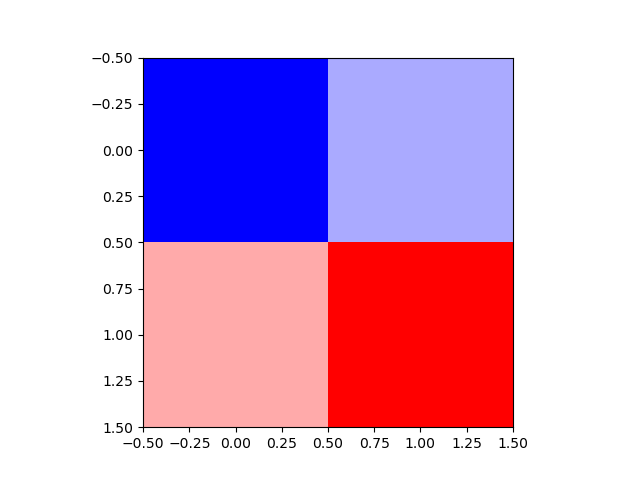
以下の例では、カラーマップを指定して2×2=4要素の2次元配列を表示している。最小値0がカラーマップbwrの青に、最大値255が赤に対応し、その間の数値の大きさに応じたカラーマップ上の色が選択されている（デフォルトのcmapはvirいdis）。

なお、この例ではpyplotから直接imshow()を実行している。

レンジ

imshow()に配列を渡して描画させるとき、数値のレンジに留意する必要がある。

デフォルトでは、imshow()は渡された配列の中の最小値と最大値をカラーマップの下限値と上限値に対応させ、線形にマッピングする。

なお、この例ではarray-likeとして2次元のリストを渡していて、Axesからimshow()を呼び出している。

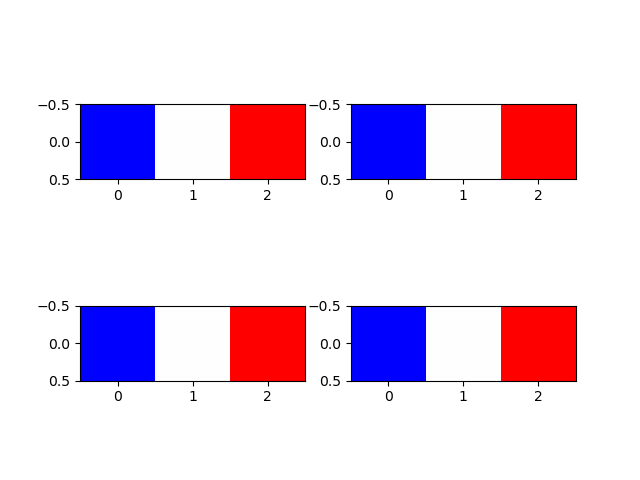
4つの配列はそれぞれ最小値と最大値が異なり、かつその中央の値を持つ。値は異なるが全て最小値がカラーマップbwrの下限値に対応する青、最大値が上限値に対応する赤、中央値は白となっている（特段フランス国旗を意図したものではない）。

viminとvmax

imshow()の引数でvminとvmaxを設定すると、配列の値に関わらず、vminとvmiaxをカラーマップの下限値と上限値に対応させる。

以下の例では最小値0、最大値1の2要素の配列を、vminとvmaxを変えてカラーマップbwrで描画させている。

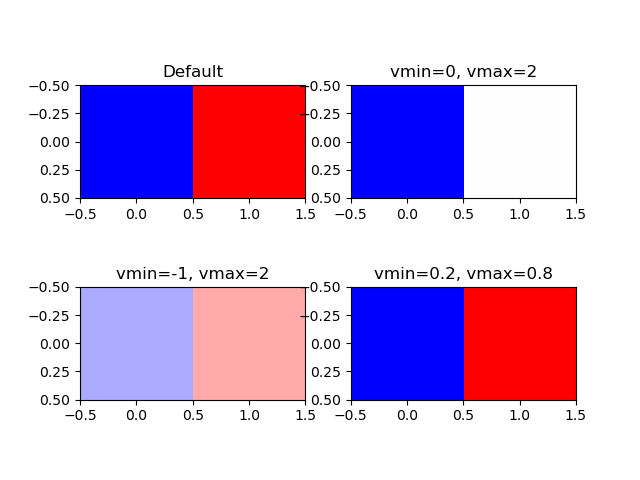
左上はデフォルトなので、最小値0がカラーマップ下限値に対応した青に、最大値1が上限値に対応した赤になっている。

右上はvmin=0で配列の最小値0と同じだが、vmax=2としている。このため配列の0はカラーマップ下限の青で、配列の1はカラーマップ中央の白になっている。

左下はvmin=-1も設定されているので、配列の0、1はカラーマップの左から1/3、2/3に相当する色となっている。

右下はvminとvmaxが配列の最小値と最大値の範囲より内側にある。このため、配列の最小値・最大値はそれぞれカラーマップの下限・上限に対応する青・赤となっている。

RGB

array-likeの次元が3次元になると、RGB/RGBA形式だと認識される。

[rows, cols, 3]
3次元目のサイズが3の時はRGB表現と認識される。1次元目と2次元目はそれぞれ画像の行数と列数とみなされ、3次元目は3つの列がR, G, Bの値に対応する。
[rows, cols, 4]
3次元目のサイズが4の時はRGBA表現と認識される。1次元目と2次元目はそれぞれ画像の行数と列数とみなされ、3次元目は3つの列がR, G, Bの値に対応し、4つ目の列が透明度に対応する。

R, G, B, Aの値は、配列のdtypeがint形式の時には0～255、floatの時には0～1の範囲が想定される。

以下の例の内容。

  • 画像サイズを2行×4列として、R, G, Bごとに画像のピクセルデータを設定→shape=(3, 2, 4)
  • ピクセル並び替え後の配列を4つ準備
  • forループでピクセル並び替え
  • 画像表示とデータ内容の表示

3次元配列のピクセルの並び替えは、泥臭くforループで回しているが、もっとエレガントな方法があるかもしれない（もとから(3, rows, cols)の形にしてくれればよかったのに）。

 

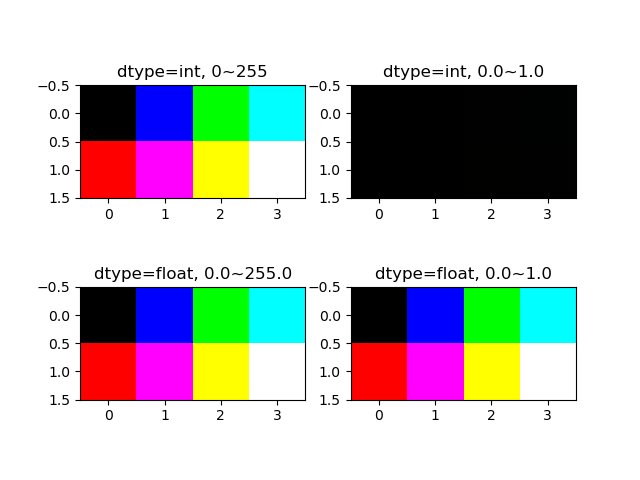
imshow()に渡す配列のdtypeがint型の時は、ピクセルデータのレンジが0～255になる。

  • 左上は元の配列のままR, G,Bが0か255なので、想定した組み合わせの色となっている
  • 右上は想定されているレンジに対して0.0～1.0の値を与えていることから、どのピクセルともR, G, Bが0か1（ほぼゼロ）となり黒くなっている（そのまま実行され、特にメッセ維持は出ない）

配列のdtypeがfloatの時は、ピクセルデータの想定レンジは0.0～1.0になる。

  • 左下は最小値0と最大255を与えているが、結果は左上と同じで、imshow()のデフォルトのレンジ0～255に変更されているようである（特にメッセージは出ない）
  • 右下は与えるピクセルデータを0.0～1.0としたところ、”入力データをクリップしている”というメッセージが出たが、レンジが修正されたらしく結果は意図通り

並べ替えた後の配列は、直感的にはわかりにくい形になっている。

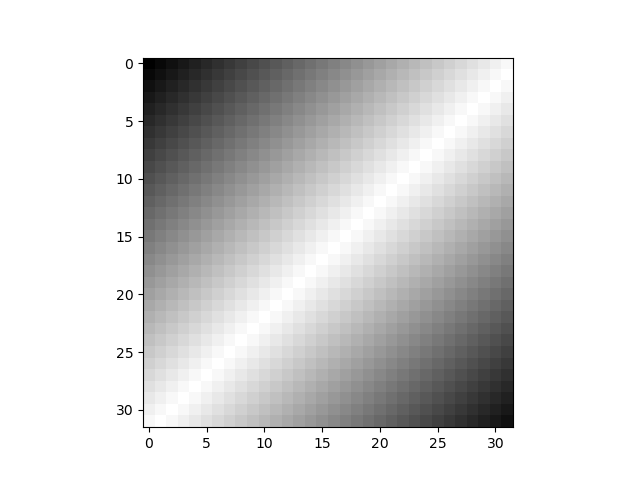
グレースケール

グレースケールの場合は、cmap='gray'を指定する。vmin、vmaxは省略しても同じ結果となるが念のため。

 

PCA – Boston house-pricesデータセット

/ tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をBiston housing pricesデータに適用して、その挙動を確認する。

主成分が適切に発見されてよい相関が得られることを期待したが、IrisデータやBreast cancerデータの場合のようなクラス分類データにおける良好な結果は得られなかった。

ただし、Boston housing pricesデータはIrisやcancerのデータよりも複雑な社会行動に関するものであり、その指標も限定されていることから、これをもってPCAが回帰系のデータに不向きとまでは言い切れない。

なお、Boston housing pricesデータの特徴量には属性データ（カテゴリーデータ、クラスデータ）が含まれることから、DataFrameのget_dummis()メソッドによるone-hot encodingを行っている。

計算の手順

  1. 必要なパッケージをインポート
  2. Boston housing pricesデータセットを準備
  3. データセットをスケーリング／エンコーディング
    1. 属性データの列を取り出して、get_dummiesでone-hot化
    2. StandardScalerで残りの特徴量データを標準化
    3. 上記2つを結合して前処理済みデータとして準備
  4. PCAモデルのインスタンスを生成
    • 引数n_components=2として、2つの特徴量について計算
  5. fit()メソッドにより、モデルにデータを学習させる
  6. 主成分やその寄与率を確認
    • 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
  7. transform()メソッドによって、主成分に沿ってデータを変換
  8. 3つの主成分について3次元可視化
  9. 2つの主成分について2次元可視化

前処理

特徴量のうちの1つCHASについては、「チャールズ川に関するダミー変数（1：川沿い、0：それ以外）」～”Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)“となっていて、0か1の属性変数である。この変数をDataFrameのget_dummies()メソッドでone-hot化する。

また、その他のデータについてはStandardScalerで標準化する。

  1. CHASのデータのみone-hot化
  2. CHASの列を除いたデータをStandardScalerで標準化
  3. 上記2つのデータをjoin()で結合

可視化

2次元

ここではまず、2次元可視化の結果を確認する。

クラス分類の場合は2次元で2つの主成分を確認できるが、回帰データの場合はターゲットの量を確認する必要があるため、グラフの軸を1つ消費する。このため、2次元による表現では1つの主成分による説明性を確認することになる。

  • 各点の色や大きさをターゲットの値によって変化させ、2つの軸を2つの主成分に割り当てる方法も考えられるが、直感的にとらえにくくなる。

この結果を見る限り、あまり美しい結果とはなっていない。データを俯瞰した際、各特徴量であまりいい説明ができなかったが、その中でもある程度関係がみられたMDEVやLSTATとの相関と変わらないくらい。

3次元

そこで3次元の可視化にして、2つの主成分による説明性を確認する。

これでもあまりいい結果にならない。ただしグラフを見ると、大きく2つの塊に分かれているように見える。ターゲットである住居価格とは別に、特徴量の組み合わせに隠れている、性質の違うグループがあるのかもしれない。

主成分と寄与率

2つの主成分と寄与率について表示させてみる。

寄与率は第1主成分が50%程度で低いため高い相関が出ないといえるかもしれない。だが、Breast cancerデータセットのクラス分類では第1主成分の寄与率が40%台だが、明確なクラス分類ができていた。やはり回帰系の問題にはPCAは不向きなのかもしれない。

主成分の要素について、先の散布図が第1主成分と負の相関があることから、第1主成分の各特徴量は価格低下に寄与するものはプラス、価格上昇に寄与するものはマイナスとなるはずである。

たとえばZNやRMがマイナスなのは頷けるが、DISがマイナスなのは微妙。TAXやPRATIOがプラスなのも逆のような気がする。

先にも書いたが、Boston housing pricesデータセットで取りそろえられた特徴量は、住居の価格以外の何かを特徴づける傾向が強いのかもしれない。

 

PCA – Breast cancerデータセット

/ tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をBreast cancerデータセットに適用して、その挙動を確認する。

30個の特徴量（全て連続量）を持つ569個の腫瘍データについて、悪性(marignant)／良性(benign)がターゲットとして与えられている。PCAによって特徴量のみの分析で、少ない主成分によってある程度明確な分離が可能なことが示される。

手順

以下の手順・コードで計算した。

  1. パッケージをインポート
  2. Breast cancerデータセットを準備
  3. データセットをスケーリング
    • StandardScalerで特徴量データを標準化している
  4. PCAモデルのインスタンスを生成
    • 引数n_components=3で3つの主成分まで計算させている
  5. fit()メソッドによって、モデルにデータを学習させる
  6. 成分やその寄与率を確認
    • 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
  7. transform()メソッドによって、主成分に沿ってデータを変換
  8. 3つの主成分について3次元可視化
  9. 2つの主成分について2次元可視化

主成分と寄与率

以下に主成分と寄与率を計算するまでのコードを示す。

寄与率は第1主成分が44%、第2主成分が19%、第3主成分が9%。第3成分まで3/4の情報を説明していることになる。

また、第1主成分は全ての特徴量がプラス方向で寄与している。

主成分をヒートマップで視覚化してみると、各主成分の符号や大きさが直感的に把握しやすくなるが、第2～第3主成分がmeanとworst系の特徴量が小さい方が影響が大きい点、3つの主成分についてerrorが大きいほど影響が大きい点など、意味づけは難しい。

可視化

3次元

3つの主成分について3次元で可視化してみると、悪性／良性がかなりはっきりと分離されている。

2次元

2つの主成分のみでも、悪性／良性がよく区分されている。

まとめ

Irisデータの場合と同じく、特徴量分析のみでクラスの別がよくあぶりだされている。

 

PCA – Irisデータセット

/ tau / コメントする

概要

scikit-learnの主成分分析モデル(PCA)をIrisデータに適用して、その挙動を確認する。

クラス分類のターゲットを用いていないにもかかわらず、少ない主成分でクラスがかなり明確に分類されることがわかる。

計算の手順

以下の手順・コードで計算した。

  1. 必要なパッケージをインポート
  2. Irisデータセットを準備
  3. データセットをスケーリング
    • StandardScalerで特徴量データを標準化している
  4. PCAモデルのインスタンスを生成
    • 引数n_componentsを指定せず、4つの特徴量全てを計算
  5. モデルにデータを学習させる
    • fit()メソッドのみでよいが、後のグラフ化のためにfit_transform()メソッドを実行
    • X_transに主成分によって変換したデータを格納
  6. 主成分やその寄与率を確認
    • 主成分はPCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
  7. 3つの主成分について3次元可視化
  8. 2つの主成分について2次元可視化

主成分と寄与率

以下に、主成分と寄与率を計算するまでのコードを示す。

寄与率の方を見てみると、第1主成分で約73%、第2主成分で23 %と、2つの主成分で特徴をほぼ説明しきっている（第3、第4主成分の寄与はほとんど無視できる）。

第1主成分の各要素の符号を見てみる。萼の長さ、花弁の長さと幅は同程度でプラス方向に効いていて、萼の幅はマイナス方向の効果を持っている。このことから、萼の細長さと花弁の全体的な大きさによって、アヤメの花が特徴づけられていると考えられる。また第2主成分は、萼の幅で殆ど特徴が決まっている。

可視化

3次元

4つの主成分のうち3つについて3次元で可視化してみると、3つのアヤメの種類がかなりきれいに分離されているのがわかる。

2次元

第2主成分まででほとんどの特徴を説明できそうなので、2次元の散布図で表示してみる。

実際、2つの主成分だけでかなりきれいに3つのクラスが分かれている。少し重なっている部分があるが、先の主成分を3つの3次元グラフで傾きを調整すると、より明確にクラスが分けられる。

なお今回の計算では、PCAのモデルインスタンス生成時にn_components=2としている。その結果は以下の通りで、1つ前の結果と同じ値になっている。

主成分分析の特徴

IrisデータセットへのPCAの適用結果から、以下のようにまとめられる。

  • 主成分分析の計算において、ターゲットのクラス分類は全く用いていない（特徴量データのみを用いている）
  • ターゲットのクラス分類は、散布図を描くときの色分けにのみ利用している
  • それにも関わらず、散布図において3つのクラスがかなりきれいに分離されている
  • 特徴量の線形和に沿った分散の最大化、という問題設定で、その背後にあるアヤメの種類がうまく分類されている

 

主成分分析の定式化

/ tau / コメントする

概要

主成分分析では、複数の特徴量を持つデータセットから、そのデータセットの特徴を最もよく表す特徴量軸を発見していく。

ここで「特徴を最もよく表す」ことを数学的に「最も分散が大きくなる」と定義する。そして、分散が最も大きくなるような方向を探すことを目的とする。

ある軸に沿った分散が大きくなるということは、その軸に沿った性質のバリエーションが多いことになる。逆に分散が小さい場合は、その性質を表す数量によっては各データの特徴の違いが判別しにくい。

主成分分析では、分散が最大となるような軸の方向を発見することが目的となる。この軸は元の特徴量の線形和で表現されるもので、各特徴量の係数は、それぞれの特徴量の寄与を表す。

(1)   \begin{align*} \boldsymbol{v} &= a_1 \boldsymbol{x}_1 + \ldosts + a_m \boldsymbol{x_m} \\ &= a_1 \left( \begin{array}{c} \x_1 \\ 0 \\ \vdots \\ 0 \end{array} \right) + \cdots + a_m \left( \begin{array}{c} 0 \\ \vdots \\ 0 \\ x_m \end{array} \right) \\ v &= | \boldsymbol{v} | = a_1 x_1 + \cdots + a_m x_m \end{align*}

以後、複数の特徴量を持つデータを、特徴量を成分とするベクトルでx表し、多数のベクトルデータxiがデータセットを構成しているとする。

最大化すべき分散の導出

多数のデータの中のデータiが空間内の点に対応し、その位置ベクトルをxiであるとする。このxiの成分が特徴量に対応する。長さが1のあるベクトルdが与えられたとき、xiのdへの射影の長さは以下のように計算される。

(2)   \begin{align*} x_{i | \boldsymbol{d}} = {\boldsymbol{x}_i}^T \boldsymbol{d} = \boldsymbol{d}^T \boldsymbol{x}_i \quad (| \boldsymbol{d} | = 1) \end{align*}

たとえば特徴量が2つなら、2次元で以下のような計算になる。

(3)   \begin{align*} \boldsymbol{x}_i = \left( \begin{array}{C} x_{i1} \\ x_{i2} \end{array} \right) , \quad \boldsymbol{d} = \left( \begin{array}{C} d_1 \\ d_2 \end{array} \right) \end{align*}

(4)   \begin{align*} x_{i | \boldsymbol{d}} = ( d_1 , d_2 ) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) = ( d_1 x_{i1} + d_2 x_{i2} ) \end{align*}

n個のデータ(i = 1～n)について、射影の平均は以下のように計算される。これは全データのベクトルdの方向に沿った値の平均となる。

(5)   \begin{align*} E( x_{i | \boldsymbol{d}} ) = E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) = \boldsymbol{d}^T E \left( \boldsymbol{x}_i \right) = \boldsymbol{d}^T \boldsymbol{\mu}_i \end{align*}

これも2次元の場合で確認すると以下の通り。

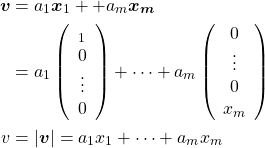
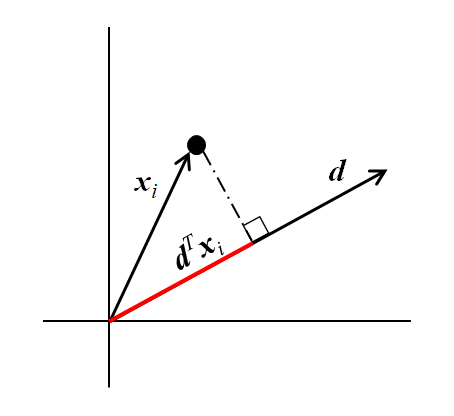
(6)   \begin{align*} E(x_{i | \boldsymbol{d}} ) &= E\left[ (d1, d2) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) \right] = (d_1, d_2) \left( \begin{array}{c} E(x_{i1}) \\ E(x_{i2}) \end{array} \right) \\ &= (d_1, d_2) \left( \begin{array}{c} \mu_{i1} \\ \mu_{i2} \end{aray} \right) \end{align*}

式(5)を使ってベクトルdの方向に沿ったデータの分散を計算する。

(7)   \begin{align*} V( x_{i | \boldsymbol{d}} ) &= V \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \\ &= E \left[ \left( \boldsymbol{d}^T \boldsymbol{x}_i - E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \right)^2 \right] \\ &= E \left[ \left( {\boldsymbol{d}}^T \left( \boldsymbol{x}_i - E(\boldsymbol{x}_i) \right) \right)^2 \right] \\ &= E \left[ {\boldsymbol{d}}^T (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \boldsymbol{d} \right] \\ &= \boldsymbol{d}^T E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \boldsymbol{d} \\ &= \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \end{align*}

中央の平均の項が共分散行列Σとなっていることに留意。これより、あるベクトルが与えられたとき、その方向に沿った全データの成分の分散が、そのベクトルと元のデータの共分散行列を使って求めることができる。

こちらを2次元で確認すると以下の通り。

(8)   \begin{align*} &E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \\ &= E \left[ \left( \begin{array}{c} x_{i1} - \mu_1 \\ x_{i2} - \mu_2 \end{array} \right) (x_{i1} - \mu_1, x_{i2} - \mu_2) \right] \\ &= \left[ \begin{array}{cc} (x_{i1} - \mu_1)^2 & (x_{i1} - \mu_1)(x_{i2} - \mu_2) \\ (x_{i2} - \mu_2)(x_{i1} - \mu_1) & (x_{i2} - \mu_2)^2 \end{array} \right] \end{align*}

分散の最大化

式(8)で計算された分散が最大となるようにベクトルdの方向を決定する。このとき、dの大きさが1であるという制約条件があるため、問題は制約条件付きの最大化問題となる。

(9)   \begin{gather*} {\rm max} \quad \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \quad \rm{s.t.} \; | \boldsymbol{d} | = 1 \end{gather*}

これをLagrangeの未定乗数法で解いていく。。

(10)   \begin{gather*} L( \boldsymbol{d}, \lambda ) = \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} - \lambda (|\boldsymbol{d}|^2 - 1) = 0 \\ \frac{\partial L}{\partial d_i} = 0 \quad ( {\rm for \; all} \; i ) \end{gather*}

Lagrange関数の第1項については、

(11)   \begin{align*} \boldsymbol{d}^T \boldsymbol{\Sigma} &= \begin{array}{ccc} ( & d_1 V_1 + \cdots + d_n C_{n1} & , \\ & \vdots & ,\\ & d_1 C_{1j} + \cdots + d_n C_{n, j} & , \\ & \vdots & ,\\ & d_1 C_{1n} + \cdots + d_n V_n & ) \end{array} \end{align*}

より、以下のような長い式になる。

(12)   \begin{align*} \boldsymbol{d}^T \boldsymbol{\Sigma d} &= \begin{array}{c} {d_1}^2 V_1 + \cdots + d_j d_1 C_{j1} + \cdots + d_n d_1 C_{n1} + \\ \vdots \\ d_1 d_j C_{1j} + \cdots + {d_j}^2 V_j + \cdots + d_n d_j C_{nj} + \\ \vdots \\ d_1 d_n C_{1n} + \cdots + d_j d_n C_{jn} + \cdots + {d_n}^2 V_n \end{array} \end{align*}

また第2項の括弧の中については以下のようになる。

(13)   \begin{align*} | \boldsymbol{d} |^2 - 1 = ( {d_1}^2 + \cdots + {d_j}^2 + \cdots + {d_n}^2 ) -1 \end{align*}

これらを前提に、Lをdjで微分すると以下のようになる。

(14)   \begin{align*} 2 d_1 C_{1j} + \cdots + 2 d_j V_{j} + \cdots 2 d_n C_{2j} - 2 \lambda d_j = 0 \end{align*}

全てのdjについて考慮した連立方程式を行列形式で表すと以下のようになる。

(15)   \begin{gather*} \boldsymbol{\Sigma d} = \lambda \boldsymbol{d} \\ | \boldsymbol{d} | = 1 \end{gather*}

1つ目の式は共分散行列に関する固有値問題の式で、di (i=1～n)とλのn+1個の変数に対してn個の式となる。これに先ほど脇に置いていたdの大きさに関する制約式を加えて式の数もn+1個となり、dとλが求められる。

特徴量が2つの場合

特徴量が2つの場合を考え、以下のように記号を定義する。

(16)   \begin{align*} \boldsymbol{\Sigma} = \left( \begin{array}{cc} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{array} \right) , \quad \boldsymbol{d} = \left( \begin{array}{c} d_1 & d_2 \end{array} \right) \end{align*}

このとき、分散を最大化する方向の単位ベクトルdを求める方程式は以下のようになる。

(17)   \begin{equation*} \left\{ \begin{array}{l} \left( \begin{array}{cc} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{array} \right) \left( \begin{array}{c} d_1 & d_2 \end{array} \right) = \lambda \left( \begin{array}{c} d_1 & d_2 \end{array} \right) \\ {d_1}^2 + {d_2}^2 = 1 \end{array} \right. \end{equation*}

1つ目の式を解くと、

(18)   \begin{equation*} \left\{ \begin{array}{l} \sigma_{11} d_1 + \sigma_{12} d_2 = \lambda d_1 \\ \sigma_{21} d_1 + \sigma_{22} d_2 = \lambda d_2 \end{array} \rhight. \end{equation*}

この方程式は不定なのでd1、d2それぞれは求められないが、μ = d2/d1は計算できる。これは固有ベクトルの方向が定まる。具体的には下記の通り。

(19)   \begin{gather*} \left\{ \begin{array}{l} \sigma_{11} + \sigma_{12} \mu = \lambda \\ \sigma_{21} + \sigma_{22} \mu = \lambda \mu \end{array} \right. \\ \lambda = \sigma_{11} + \sigma_{12} \mu = \frac{\sigma_{21}}{\mu} + \sigma_{22} \\ \sigma_{12} \mu^2 + ( \sigma_{11} - \sigma_{22} ) \mu - \sigma_{21} = 0 \end{gather*}

これを解いてベクトルdの方向が定まる。これに制約条件|d|2 ＝１を加味することで、大きさ1の単位ベクトルとしてdが決定される。

この解き方は最大化問題ではないので、連立方程式から2つの固有ベクトルと固有値が求まる。

第2主成分以降

一般的な固有値問題では、元の変数と同じ数の固有ベクトルと固有値のセットが求まるが、最大化問題として解いた場合には主成分が1つだけ求まる。

scikit-learnのPCAインスタンス生成時にn_componentsで主成分の数に制約をかけることができるが、このことから、PCA.fit()の実行時には連立方程式を解いているのではなく、最大化問題で1つずつ主成分を計算しているのではないかと思われる。

第2主成分以降の計算についての紹介はあまり見られないが、以下の手順と考えらえれる。

  1. 各データについて、第1主成分の方向への射影を計算
  2. その射影の符号を逆にしたベクトルを各データに加える
  3. これで第1主成分に沿ったばらつきが全てゼロになるので、残りの成分の中で最大となるベクトルの方向を計算し、第2主成分とする
  4. 以上を繰り返し、順次最大主成分沿いの情報を消しながら、各主成分を計算

主成分の意味

主成分の意味の一つに、元のデータを構成する成分という捉え方がある。

たとえば特徴量の数がnである元データXがあり、主成分の数をm(<= n)でモデルを構築するとする。scikit-learnでPCAのインスタンスを生成するのにn_components=mと指定し、fit(X)を実行すると、m個の主成分が生成される。この主成分は共分散行列に対する固有ベクトルであり、要素数n個（特徴量数に等しい）の1次元配列がm行（主成分の数に等しい）並んだ2次元配列として、PCAインスタンスのプロパティーcomponents_に保存される。

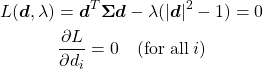
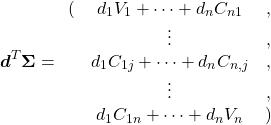
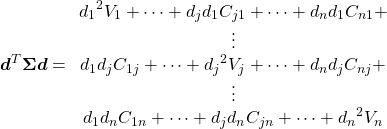
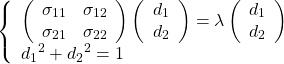
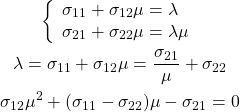
(20)   \begin{equation*} \tt{components\_} = \left[ \begin{array}{ccc} (p_{0, 0} & \cdots & p_{0, n-1} ) \\ & \vdots &\\ (p_{m-1, 0} & \cdots & p_{m-1, n-1}) \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{p}_0 \\ \vdots \\ \boldsymbol{p}_m \end{array} \right] \end{equation*}

元のデータは、各主成分（固有ベクトル）の重み付き和として表現される。

(21)   \begin{equation*} \boldsymbol{x} = (x_0, ..., x_n) = a_0 \boldsymbol{p}_0 + a_1 \boldsymbol{p}_1 + a_2 \boldsymbol{p}_2 + \cdots \end{equation*}

この様子を2次元で示したのが以下の図で、直行する2つの主成分から元データの１つxが定まる。

xの主成分1、2の方向の大きさはxの各主成分に対する射影で、それらの長さはxと各主成分の内積で得られる。

(22)   \begin{equation*} \boldsymbol{x} = (x_0, ..., x_n) = ( \boldsymbol{x} \cdot \boldsymbol{p}_0 ) \boldsymbol{p}_0 + ( \boldsymbol{x} \cdot \boldsymbol{p}_1 ) \boldsymbol{p}_1 + ( \boldsymbol{x} \cdot \boldsymbol{p}_2 ) \boldsymbol{p}_2 + \cdots \end{equation*}

 

DataFrame – get_dummies – One-hot

/ tau / コメントする

概要

DataFrameのget_dummies()メソッドは、属性データ（カテゴリーデータ）をone-hot-encodingの形に変換してくれる。

Scikit-learnにもOneHotEncoderがあるが、get_dumies()はデータの切り貼りをせずにダイレクトに属性変数だけをone-hotの形にしてくれるので便利。

基本

get_dumies()の引数にDataFrameを指定すると、文字列で属性指定されたデータが自動で認識されてon-hotの形に変換される。

分解された列名は、"元の列名_属性名"となり、それぞれに対応する属性の列のみが1、その他の列は0となる。列の並びは、属性名の辞書順。数値データの列は無視される。

属性データが複数列の場合

文字列の属性データが複数列ある場合も、自動的にone-hotに分解してくれる。

属性が数値表現の場合

属性値が文字列ではなく数値表現の場合、get_dummies()の引数に単にDataFrameを渡すだけでは変換してくれない（通常の数量データとして認識される）。

そこで、変換したい列をcolumns引数で指定する。

複数の属性データの列がある場合、columns引数でリスト指定する。

属性名の指定

prefix引数で文字列を指定すると、属性名がその文字列で置き換えられる。ただし複数の属性列が全て同じ文字列になる。

属性列ごとにprefixを変えて指定したい場合はリストで指定。

 

DataFrame – データの概観

/ tau / コメントする

概要

DataFrameの規模、格納されているデータの概要や基礎統計量を概観する各種の手順。Scikit-learnのBoston housingデータセットを例にする。

DataFrameの規模・形状

sizeプロパティーで全データ数、shapeプロパティーで行数と列数を確認。

データの先頭部分と末尾部分

head()メソッド／tail()メソッドで先頭／末尾の5行分が得られる。引数で抜き出す行数を指定。

info()～各列の基本情報の表示

info()メソッドは、DataFrameの概要に関する概略情報を出力する。直接標準出力にプリントする点に注意。

たとえば一部にNaNが含まれる場合の出力は以下のようになる。

dscribe()～基本的な統計量

describe()メソッドは、各列のデータについて、個数や平均といった基本的な統計量を計算する。

特定の列の統計量を見たいときは列を指定。

なおstd（標準偏差）については、ddof=1を指定した結果と同じであり、n−1で割った不偏分散。

全ての列を見たいときには、set_option()メソッドの引数でdisplay.max_columnsパラメーターを指定する。初期値に戻すときはreset_option()メソッド。

属性変数のカウント

属性変数の属性値のカウントには、value_counts()メソッドを使う。このメソッドは、ユニークな値の数をカウントして集計する。

2つの属性変数をファンシーインデックスで指定すると、「2つの属性のユニークな組み合わせ」の数が集計される。

 

Python – 平均・分散・共分散

/ tau / コメントする

1次元配列の場合

平均

平均はmean()メソッドで計算。

分散・標準偏差

標本分散・標本標準偏差

分散はvar()メソッド、標準偏差はstd()メソッドで計算。デフォルトでは標本分散と標本標準偏差。

不偏推定量

分散の算出では、引数ddof (delta degrees of freedom)で指定した引数をデータ数nから引いた数で偏差の二乗和を割る。デフォルトではddof=0なので標本分散、標本標準偏差になるが、ddof=1を指定すると、不偏分散、標準偏差の不偏推定量が計算される。

2次元配列の場合

平均

平均はmean()メソッドで計算。引数axis=0/1で列方向／行方向の計算方向を指定。計算結果は1次元配列で、要素数は列方向の平均なら行数、行方向の平均なら列数と同じになる。

分散・標準偏差

標本分散・標本標準偏差

分散はvar()メソッド、標準偏差はstd()メソッドで計算。デフォルトでは標本分散、標本標準偏差を計算。デフォルトでは標本分散、標本標準偏差。

不偏推定量

引数ddof=1を指定すると、データ数nからddof=1を引いた数で偏差の二乗和が割られ、不偏分散、標準偏差の不偏推定量が計算される。

共分散

cov()メソッドで二つのデータの共分散行列を計算する。結果は2次元配列で得られ、対角要素は各データの分散、対角要素以外の要素は行数・列数に対応する共分散。

デフォルトでは引数bias=Falseとなっていて、偏差の積和をn−1で割った不偏推定量が計算される。

bias=Trueを指定すると、偏差の積和を割る数がnとなり、標本に対する分散・共分散が計算される。

 

感度＝陽性的中率の特性

/ tau / コメントする

概要

機械学習のモデルの性能や感染症検査の確からしさを検証する際、陽性的中率（適合度）や陰性的中率を確認すべきだが、これらの値が、そもそものデータの特性やモデル／検査の性能によってどのように変化するかを確認する。

具体的には、注目事象の率と真陽性率（感度）・真陰性率（特異度）を変化させたときの、陽性的中率・陰性的中率の変化を見る。

これらの値の意味や計算方法については、Confusing matrixを参照。

その結果から、以下のようなことがわかった。

  • 予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
  • 特異度を向上させることで適合度は大きく向上する
  • ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

2020年現在、世界的に大きな影響を及ぼしているCOVID-19（新型コロナウィルス）感染症のPCR検査では、一般に感度が70％程度、特異度が90％以上、陽性的中率が数%程度という値が多い。感度が7割程度というのは少し低く、陽性的中率がそもそも小さすぎるという気がしていたが、上記のことと符合することがわかった。

指標

以下の指標を、目的として計算する指標とする。

  • PPV(Positive Predicted Value)：陽性的中率、適合度、Precision
  • NPV(Negative Predicted Value)：陰性的中率

これらの指標を計算するために用いる指標は以下の通り。

  • TR(Target Rate)：注目事象の全体比率（ターゲット比率）
  • TPR(True Positive Rate)：真陽性率、感度(Sencitivity)
  • TNR(True Negative Rate)：真陰性率、特異度(Specificity)

例えば感染症の例で言うと、有病率(TR)、検査の感度(TPR)、特異度(TNR)がわかっているときに、陽性的中率(PPV)、陰性的中率(NPV)を求めることに相当する。

PPV・NPVの計算式の導出

元データの構成

まず、confusing matrixを以下のように表現する。これは、データ数で表現されたテーブルの各要素を全データ数で割った率で表すことに相当する。

    \begin{align*} \begin{array}{cc|cc|c} & & \mathrm{Prediction}\\ & & \mathrm{Positive} & \mathrm{Negative} & \mathrm{Sum} \\ \hline \mathrm{Fact} & \mathrm{Positive} & tp & fn & r_1 \\ & \mathrm{Negative} & fp & tn & r_2 \\ \hline & \mathrm{Sum}& c_1 & c_2 & 1 \end{array} \end{align}

PPV・NPVの計算式

まず、事実(Fact)がpositiveである率がr1に相当し、これはTR (target rate)に等しい。このTRと率TPRを使って、Positiveの行のtp(true positive)とfn (false negative)の率を計算。

(1)   \begin{align*} r_1 &= TR \\ tp &= r_1 \cdot TPR = TR \cdot TPR \\ fn &= r_1 \cdot (1 - TPR) = TR (1 - TPR) \end{align*}

2行目の合計r2については、行和の合計が1になることから以下のように計算される。

(2)   \begin{align*} r_2 &= 1 - r_1 = 1 - TR \end{align*}

このr2と率TNRからNegativeの行のtn(true negative)とfp (false positive)を計算。

(3)   \begin{align*} tn &= r_2 \cdot TNR = (1 - TR) TNR \\ fp &= r_2 (1 - TNR) = (1 - TR) (1 - TNR) \end{align*}

tpとfpからc1を、tnとfnからc2を計算。

(4)   \begin{align*} c_1 &= tp + fp = TR \cdot TPR + (1 - TR) (1 - TNR) \\ c_2 &= tn + fn = (1 - TR) TNR + TR (1 - TPR) \end{align*}

PPV（陽性的中率、感度）はc1に対するtpの率で計算される。以下の式は分数の分数で若干ややこしいが、3つの指標が1回ずつ現れ、整った形になる。

(5)   \begin{align*} PPV &= \frac{tp}{c_1} = \frac{TR \cdot TPR}{TR \cdot TPR + (1 - TR) (1 - TNR) } \\ &= \frac{1}{1 + \left(\dfrac{1}{TR} - 1 \right) \dfrac{1 - TNR}{TPR}} \end{align*}

NPV（陰性的中率、特異度）はc2に対するtnの率で計算される。以下の式とPPVの式を比べると、はTRの分数項ついて逆数であり、TPRとTNRが入れ替わっていて、PPVとNPVで対称性がある。

(6)   \begin{align*} NPV &= \frac{tn}{c_2} = \frac{(1 - TR) TNR}{(1 - TR) TNR + TR (1 - TPR)}\\ &= \frac{1}{1 + \dfrac{TR}{1 - TR} \dfrac{1 - TPR}{TNR}} \end{align*}

パラメーターに応じたPPV・NPVの変化

PPV

上記の結果を用いて、ターゲット比率、真陽性率（感度）、真陰性率（特異度）の様々な値に対するPPV（陽性的中率）、NPV（陰性的中率の変化を観察する。

まず、ターゲット比率が1に近い（ほとんどがターゲットとなるような）状態から、ターゲットが0に近いような（ターゲットとなるデータがほとんどないような）状態の間で、PPVがどのように変化するか確認してみる。

TPR（感度）の値によって曲線の形に若干の変化はあるがあまり大きくは変わらず、むしろTNR（特異度）の値による曲線の形状の変化が大きい。ここでTRが0.1～0と小さい範囲のところを見てみる。

やはり感度の影響はあまり大きくないようである。TNRを大きくするにしたがって曲線の形状は大きく変化し、ターゲット比率が小さいところでの適合度が向上するが、ターゲット比率が0に近いところではPPVがかなり小さくなる。

次に、TPRを変化させたときの曲線の違いが分かるように、表示させる変数を入れ替えてみる。まずTRが1～0の全域。

やはり感度による曲線の変化は小さく、特異度の影響が大きい。以下のようにTRが0.1～0の範囲を拡大しても同様の傾向。

以上の結果から、以下のことが言える。

  • ターゲット比率が低くなるほどNPVは小さくなる（適合度が低くなり、予測／検査の信頼性が下がる）
  • 予測モデルや検査のTPR（感度）を上げることによるPPVの向上効果はあまり大きくない（いたずらに感度を上げても顕著な効果はない）
  • TNR（特異度）の向上によって、適合度は大きく向上する
  • ターゲット比率がとても小さい場合、その率の現象に従って適合度は急激に低下する

さらにこれを一般的な表現でまとめると、

  • 予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
  • 特異度を向上させることで適合度は大きく向上する
  • ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

NPV

PPVと同様にNPVについても計算してみた。

まずいくつかのTPRに対して、TNRを変化させて曲線を描いたもの。PPVの場合と比べて形状が左右逆で、TNRを固定してTPRを変化させたときの図と同じ傾向。

次に、いくつかのTNRを固定してTPRを変化させたもの。これもPPVと形状、TPR、TNRの関係が逆になっている。

PPVとNPVの関係

PPVとNPVが同じTPR、TNRに対してどのように変化するか重ねてみる。

TPRとTNRを同程度とすることでターゲット比率0.5付近で双方が等しくなり、その値を高くすることで、より広い範囲でPPVが向上する。

シミュレーションによる挙動確認

これまでの結果は、confusion matrixの各要素にTR、TPRなどの比率を適用してPPV、NPVを計算した。この方法は、ある予測／判定が理論通りに再現された場合だが、実際にはターゲットとなる事象の割合も、予測がpositive/negativeになる割合も確率事象である。

そこで念のため、多数の二値(True/False)正解データをランダムに生成し、これに対してTPR、TNRの設定に従った答えを出す疑似的なモデルで「予測」する。その結果を整理したconfusion_matrixからPPVを計算したのが以下の図である。

その結果は計算式による場合と同じで、理論上の挙動と実世界で起こるであろう挙動が一致している。

処理内容は以下の通り。

  • 与えられたTrue/Falseに対して、あらかじめ設定したTPR/TNRと一様乱数に従ってTrue/Falseを「予測」する疑似予測モデルを準備
  • TR=1～0の間で100個のデータについてPPVを計算する
    • 1つのTRについて10万個の2値正解データを生成
    • 正解データセットを疑似予測モデルに適用して予測データセットを得る
    • 予測データセットからconfusion matrixを構成し、その要素からPPVを計算し、配列に格納
  • 以上の結果をプロット