決定木の分割の考え方

1 決定木の分割の考え方
2 エントロピー（平均情報量）とジニ不純度
3 ノード分割の考え方～利得
4 簡単な例
- 4.1 000111と並んでいる場合
- 4.2 00100111と並んでいる場合

決定木の分割の考え方

決定木のデータを特性量によって分割するには、分割後のノードの状態ができるだけうまく分かれていることが必要となる。この「うまく分かれている」状態は、言い換えれば分割後のノード内のデータができるだけ「揃っている」ともいえる。たとえば2クラスの分類をする場合、ノード内に1つのクラスしか含まれていない場合は最も「純度が高い」状態であり、2つのクラスのデータが半分ずつ含まれている場合に最も「純度が低い」状態となる。

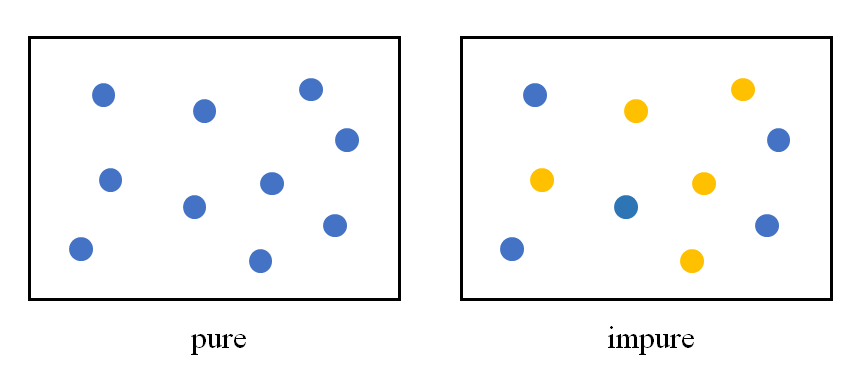
このような状態を定量的に表すのにエントロピーとジニ不純度という2つの考え方があるが、ここではそれらを確認する。

エントロピー（平均情報量）とジニ不純度

定義

クラスc = 1~Cに属するデータがノードtに属しており、各クラスごとのデータ数をn_c、データの総数をNとする。この場合、このノードの純度／不純度を表すのに、エントロピー（entropy、平均情報量）とジニ不純度（Gini impurity）という2つの考え方がある。ノードtのエントロピーをI_H(t)、ジニ不純度をI_G(t)と表すと、それぞれの定義は以下の通り。

(1) $\begin{align*} I_H(t) &= - \sum_{c=1}^C p_c(t) \log p_c(t) = - \sum_{c=1}^C \frac{n_c}{N} \log \frac{n_c}{N} \\ I_G(t) &= 1 - \sum_{c=1}^C p_c^2 = 1 - \sum_{c=1}^C \left( \frac{n_c}{N} \right)^2 \end{align*}$

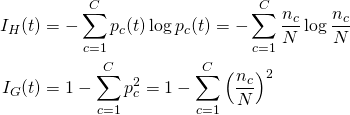
エントロピーの対数の底は何でもいいが、分類するクラス数にすると最も高いエントロピーが1になって都合がよいようだ）。

ジニ不純度については次の表現の方が直感的にわかりやすい。

(2) $\begin{equation*} I_G(t) = \sum_{c=1}^C p_c (1 - p_c) \end{equation*}$

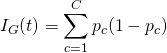
これを展開すると先のI_Gと同じ形になるが、この形だと関数形が上に凸でp_c = 0, 1でI_G = 0となることがわかる。

計算例

クラス数Cのデータについて、あるノード内のデータが全て同じクラスの場合、純度が高い／不純度が低い。

(3) $\begin{align*} I_H(t) &= - \frac{N}{N} \log_C \frac{N}{N} = 0 \\ I_G(t) &= 1 - \left( \frac{N}{N} \right)^2 = 0 \end{align*}$

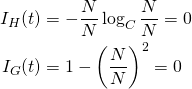
ノード内で全てのクラスのデータが同じ数ずつある場合、純度が低い／不純度が高い。

(4) $\begin{align*} I_H(t) &= - C \cdot \frac{N/C}{N} \log_C \frac{N/C}{N} = - C \cdot \frac{1}{C} \log_C \frac{1}{C} = 1 \\ I_G(t) &= 1 - C \left( \frac{N/C}{N} \right)^2 = 1 - \frac{1}{C} \end{align*}$

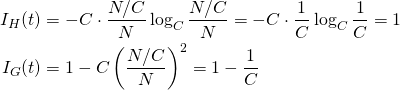
分布

あるノード内にN個の2クラスデータがあり、クラス1のデータ数をnとする。このとき、クラス1のデータの発生率pに対するエントロピー、ジニ不純度の分布は以下のようになる。

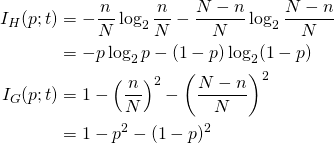
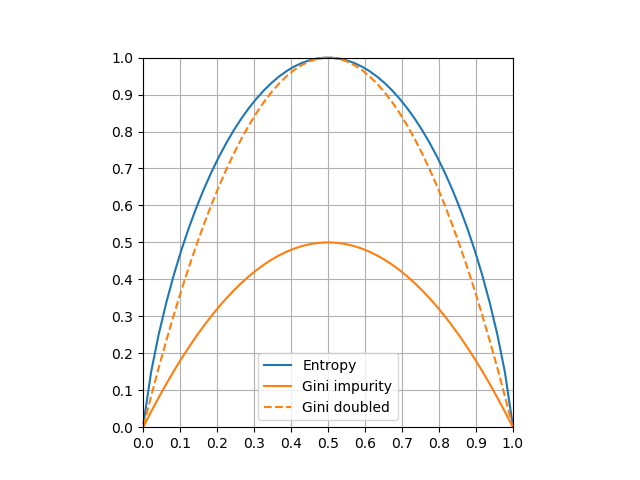
(5) $\begin{align*} I_H(p; t) &= - \frac{n}{N} \log_2 \frac{n}{N} - \frac{N-n}{N} \log_2 \frac{N-n}{N} \\ &= -p \log_2 p - (1-p) \log_2 (1-p) \\ I_G(p; t) &= 1 - \left( \frac{n}{N} \right)^2 - \left( \frac{N-n}{N} \right)^2 \\ &= 1 - p^2 - (1-p)^2 \end{align*}$

これらをグラフ化したのが以下の図。p = 0.5で双方最大値をとり、エントロピーは1 、ジニ不純度は0.5。グラフの形状を比較するため、ジニ不純度を2倍した線も入れている。

import numpy as np
import matplotlib.pyplot as plt

eps = 1e-3
p = np.linspace(eps, 1 - eps)
Ih = -p * np.log2(p) - (1 - p) * np.log2(1 - p)
Ig = 1 - p**2 - (1 - p)**2

fig, ax = plt.subplots()

ax.plot(p, Ih, c='tab:blue', label="Entropy", clip_on=False)
ax.plot(p, Ig, c='tab:orange', label="Gini impurity")
ax.plot(p, Ig*2, c='tab:orange', ls='dashed', label="Gini doubled"
    , clip_on=False)

ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xticks(np.linspace(0, 1, 11))
ax.set_yticks(np.linspace(0, 1, 11))
ax.grid(True)
ax.set_aspect('equal')
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

eps = 1e-3

p = np.linspace(eps, 1 - eps)

Ih = -p * np.log2(p) - (1 - p) * np.log2(1 - p)

Ig = 1 - p**2 - (1 - p)**2

fig, ax = plt.subplots()

ax.plot(p, Ih, c='tab:blue', label="Entropy", clip_on=False)

ax.plot(p, Ig, c='tab:orange', label="Gini impurity")

ax.plot(p, Ig*2, c='tab:orange', ls='dashed', label="Gini doubled"

, clip_on=False)

ax.set_xlim(0, 1)

ax.set_ylim(0, 1)

ax.set_xticks(np.linspace(0, 1, 11))

ax.set_yticks(np.linspace(0, 1, 11))

ax.grid(True)

ax.set_aspect('equal')

ax.legend()

plt.show()

ノード分割の考え方～利得

親ノードを子ノードに分割するのに最も妥当な分割とするには、分割後の子ノードの純度ができるだけ高くなるような特徴量を探すことになる。ある特徴量について、親ノードから子ノードに分割したときにどれだけ純度が高くなったかを比較する量として、利得（情報利得、gain）が用いられる。

親ノードt_Pにc = 1~Cのクラスのデータがそれぞれn_cずつあるとする。このときの親ノードのエントロピーI_H(t_P)、ジニ不純度I_G(t_P)は式(1)で計算される。

まずエントロピーについて考える。ある特徴量fを定めると左右のノードのデータ分布が決まり、その時の左ノードt_L、右ノードt_Lのエントロピーが以下のように計算される。

(6) $\begin{align*} & I_H(t_L) = -p_c(t_L) \sum_{c=1}^C \log p_c(t_L) = - \sum_{c=1}^C \frac{n_c(t_L)}{N(t_L)} \log \frac{n_c(t_L)}{N(t_L)} \\ & I_H(t_R) = -p_c(t_R) \sum_{c=1}^C \log p_c(t_R) = - \sum_{c=1}^C \frac{n_c(t_R)}{N(t_R)} \log \frac{n_c(t_R)}{N(t_R)} \end{align*}$

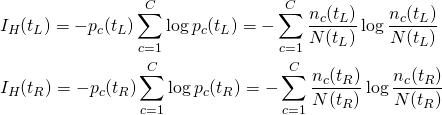
このとき、それぞれのノードのエントロピーにノードの重みw_L, w_Rを掛け、これを親ノードのエントロピーから引いた量を利得（gain、情報利得）という。重みを各ノードのデータ数の比率とすると、利得は以下のように計算される。

(7) $\begin{align*} G_H(t_P, f) &= I_H(t_P) - w_L I_H(t_L) - w_R I_H(t_R) \\ &= I_H(t_P) - \frac{n_L}{N} I_H(t_L) - \frac{n_R}{N} I_H(t_R) \end{align*}$

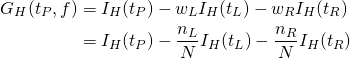
ジニ不純度についても同様の計算ができる。

(8) $\begin{align*} G_G(t_P, f) &= I_G(t_P) - w_L I_G(t_L) - w_R I_G(t_R) \\ &= I_G(t_P) - \frac{n_L}{N} I_G(t_L) - \frac{n_R}{N} I_G(t_R) \end{align*}$

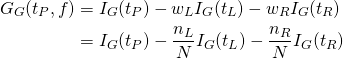
利得は、ある特徴量の値によって分割した後の状態が、分割前の状態に対してどれだけ純度が高くなったかを表す。

決定木のノードを分割するにあたっては、子ノードの純度ができるだけ高くなるように（エントロピー／ジニ不純度が小さくなるように）fを選ぶことになる。

簡単な例

特徴量が1つでデータ数が少ないケースで、利得の計算を確認してみる。

000111と並んでいる場合

クラス0、1がこのように並んでいるとき、左から境界を動かしていったときの左右のノードの不純度、利得について計算した結果は以下の通り。

IHP=1.0, IGP=0.5
[0][0 0 1 1 1]:
  IHL=-0.000, IHR= 0.971, G_H= 0.191
  IGL= 0.000, IGR= 0.480, G_G= 0.100
[0 0][0 1 1 1]:
  IHL=-0.000, IHR= 0.811, G_H= 0.459
  IGL= 0.000, IGR= 0.375, G_G= 0.250
[0 0 0][1 1 1]:
  IHL=-0.000, IHR= 0.000, G_H= 1.000
  IGL= 0.000, IGR= 0.000, G_G= 0.500
[0 0 0 1][1 1]:
  IHL= 0.811, IHR= 0.000, G_H= 0.459
  IGL= 0.375, IGR= 0.000, G_G= 0.250
[0 0 0 1 1][1]:
  IHL= 0.971, IHR= 0.000, G_H= 0.191
  IGL= 0.480, IGR= 0.000, G_G= 0.100

IHP=1.0, IGP=0.5

[0][0 0 1 1 1]:

IHL=-0.000, IHR= 0.971, G_H= 0.191

IGL= 0.000, IGR= 0.480, G_G= 0.100

[0 0][0 1 1 1]:

IHL=-0.000, IHR= 0.811, G_H= 0.459

IGL= 0.000, IGR= 0.375, G_G= 0.250

[0 0 0][1 1 1]:

IHL=-0.000, IHR= 0.000, G_H= 1.000

IGL= 0.000, IGR= 0.000, G_G= 0.500

[0 0 0 1][1 1]:

IHL= 0.811, IHR= 0.000, G_H= 0.459

IGL= 0.375, IGR= 0.000, G_G= 0.250

[0 0 0 1 1][1]:

IHL= 0.971, IHR= 0.000, G_H= 0.191

IGL= 0.480, IGR= 0.000, G_G= 0.100

この場合、当然のことながら真ん中でノードを分割することで2つのクラスがきれいに分かれ、利得もこれを表している。

00100111と並んでいる場合

今度は一部に他のクラスが紛れ込んでいる場合。左のクラス0の集団に1つだけクラス1のデータが含まれているときの挙動を確認する。

IHP=1.0, IGP=0.5
[0][0 1 0 0 1 1 1]:
  IHL=-0.000, IHR= 0.985, G_H= 0.138
  IGL= 0.000, IGR= 0.490, G_G= 0.071
[0 0][1 0 0 1 1 1]:
  IHL=-0.000, IHR= 0.918, G_H= 0.311
  IGL= 0.000, IGR= 0.444, G_G= 0.167
[0 0 1][0 0 1 1 1]:
  IHL= 0.918, IHR= 0.971, G_H= 0.049
  IGL= 0.444, IGR= 0.480, G_G= 0.033
[0 0 1 0][0 1 1 1]:
  IHL= 0.811, IHR= 0.811, G_H= 0.189
  IGL= 0.375, IGR= 0.375, G_G= 0.125
[0 0 1 0 0][1 1 1]:
  IHL= 0.722, IHR= 0.000, G_H= 0.549
  IGL= 0.320, IGR= 0.000, G_G= 0.300
[0 0 1 0 0 1][1 1]:
  IHL= 0.918, IHR= 0.000, G_H= 0.311
  IGL= 0.444, IGR= 0.000, G_G= 0.167
[0 0 1 0 0 1 1][1]:
  IHL= 0.985, IHR= 0.000, G_H= 0.138
  IGL= 0.490, IGR= 0.000, G_G= 0.071

IHP=1.0, IGP=0.5

[0][0 1 0 0 1 1 1]:

IHL=-0.000, IHR= 0.985, G_H= 0.138

IGL= 0.000, IGR= 0.490, G_G= 0.071

[0 0][1 0 0 1 1 1]:

IHL=-0.000, IHR= 0.918, G_H= 0.311

IGL= 0.000, IGR= 0.444, G_G= 0.167

[0 0 1][0 0 1 1 1]:

IHL= 0.918, IHR= 0.971, G_H= 0.049

IGL= 0.444, IGR= 0.480, G_G= 0.033

[0 0 1 0][0 1 1 1]:

IHL= 0.811, IHR= 0.811, G_H= 0.189

IGL= 0.375, IGR= 0.375, G_G= 0.125

[0 0 1 0 0][1 1 1]:

IHL= 0.722, IHR= 0.000, G_H= 0.549

IGL= 0.320, IGR= 0.000, G_G= 0.300

[0 0 1 0 0 1][1 1]:

IHL= 0.918, IHR= 0.000, G_H= 0.311

IGL= 0.444, IGR= 0.000, G_G= 0.167

[0 0 1 0 0 1 1][1]:

IHL= 0.985, IHR= 0.000, G_H= 0.138

IGL= 0.490, IGR= 0.000, G_G= 0.071

左から1つ目2つ目と境界を動かしていくと少しずつ利得が上昇するが、左側のノードにクラス1のデータが入ってきたところでその不純度が跳ね上がり、利得が下がる（8～10行目）。その後再び利得は上昇し、右側のデータがクラス1のみ3つとなった時に利得が最大となっている。このとき左側のノードにクラス1のデータが1つ含まれているが、他の4つのデータがクラスゼロと多いため、不純度は比較的低い。

利得が最大となる時でも、完全にクラスが分かれた時に比べて半分近くの利得だが、これはデータ数の多い左側に異なるクラスのデータが含まれているからと考えられる。

ここまでの計算に使ったコードは以下の通り。

import numpy as np

def impurity(node):
    N = node.size
    n0 = node[node==0].size
    n1 = node[node==1].size
    p0, p1 = n0 / N, n1 / N
    entropy = - (p0 * np.log2(p0) if p0 > 0 else 0) \
              - (p1 * np.log2(p1) if p1 > 0 else 0)
    gini = 1 - p0*p0 - p1*p1

    return entropy, gini

#node = np.array([0, 0, 0, 1, 1, 1])
node = np.array([0, 0, 1, 0, 0, 1, 1, 1])

IHP, IGP = impurity(node)
print("IHP={}, IGP={}".format(IHP, IGP))
for pos in range(1, node.size):
    node_left = node[0:pos]
    node_right = node[pos:node.size]
    node_text = "{}{}".format(node_left, node_right)
    IHL, IGL = impurity(node_left)
    IHR, IGR = impurity(node_right)
    wL = node_left.size / node.size
    wR = node_right.size / node.size
    GH = IHP - wL*IHL - wR*IHR
    GG = IGP - wL*IGL - wR*IGR
    print("{}:".format(node_text))
    print("  IHL={:6.3f}, IHR={:6.3f}, G_H={:6.3f}".format(IHL, IHR, GH))
    print("  IGL={:6.3f}, IGR={:6.3f}, G_G={:6.3f}".format(IGL, IGR, GG))

import numpy as np

def impurity(node):

N = node.size

n0 = node[node==0].size

n1 = node[node==1].size

p0, p1 = n0 / N, n1 / N

entropy = - (p0 * np.log2(p0) if p0 > 0 else 0) \

- (p1 * np.log2(p1) if p1 > 0 else 0)

gini = 1 - p0*p0 - p1*p1

return entropy, gini

#node = np.array([0, 0, 0, 1, 1, 1])

node = np.array([0, 0, 1, 0, 0, 1, 1, 1])

IHP, IGP = impurity(node)

print("IHP={}, IGP={}".format(IHP, IGP))

for pos in range(1, node.size):

node_left = node[0:pos]

node_right = node[pos:node.size]

node_text = "{}{}".format(node_left, node_right)

IHL, IGL = impurity(node_left)

IHR, IGR = impurity(node_right)

wL = node_left.size / node.size

wR = node_right.size / node.size

GH = IHP - wL*IHL - wR*IHR

GG = IGP - wL*IGL - wR*IGR

print("{}:".format(node_text))

print(" IHL={:6.3f}, IHR={:6.3f}, G_H={:6.3f}".format(IHL, IHR, GH))

print(" IGL={:6.3f}, IGR={:6.3f}, G_G={:6.3f}".format(IGL, IGR, GG))

TauStation

決定木の分割の考え方