LEDの保護抵抗

/ tau / コメントする

対象とする回路

以下のような回路を考える。

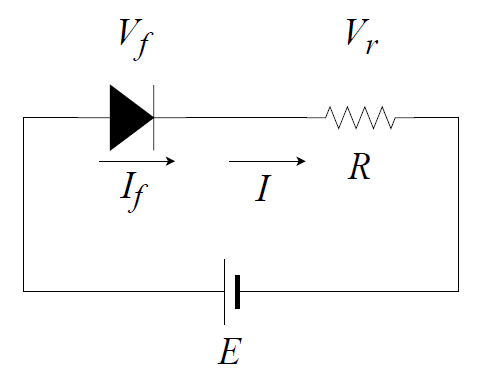
ここで各記号の意味は以下の通り。

  • E：電源電圧
  • Vf：LEDにかかる順電圧
  • If：LEDを流れる順電圧
  • Vr：保護抵抗による電圧降下
  • R：保護抵抗値
  • I：回路を流れる電流（I = If）

Vf（順電圧）やIf（順電流）は、それらを用いる人や場合によってLEDが発光し始める閾値や典型値など定義が異なっているが、ここではその時点の回路での値とする。

保護抵抗による電圧降下

保護抵抗による電圧降下、抵抗値、回路電流の間では、以下のようにオームの法則が成立する。VrはIの線形関数となっている。

(1)   \begin{equation*} V_r = R I \end{equation*}

LEDの特性

一方LEDの順電圧Vfも電流の関数だが、それは一般的な固定抵抗のものと異なり、電圧によって非線形的に電流が変化する。以下は赤色LEDの特性曲線を概ねのイメージで描いた例。

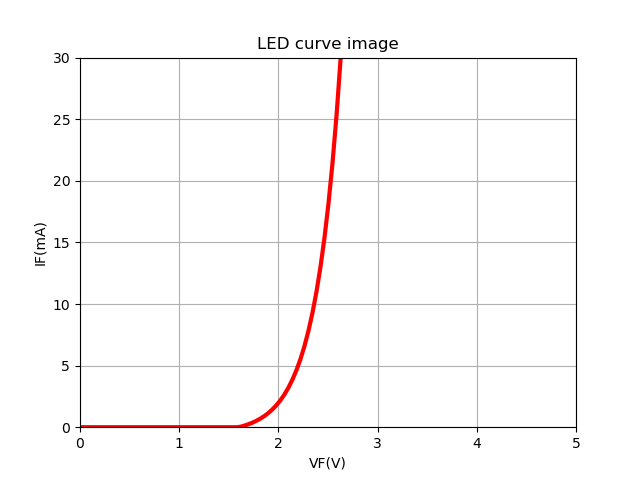
LEDの電流～電圧特性の特徴は以下の通り。

  • LEDにかかる順電圧がある閾値を越えるまでは電流は流れず発光しない
  • 順電圧が閾値を越えると、電圧値に対して急に電流が増加する
  • 順電圧の僅かな変動に対して、順電流の変動が大きい

LEDの内部抵抗で考えると以下のように表現できる。

  • 閾値以下ではLEDの内部抵抗は∞と考えてもよいくらい大きい
  • 閾値を越えると、順電圧の増加に対して内部抵抗が急激に減少していく

回路に関する計算

基礎式

LEDの順電流・順電圧に関する特性曲線をI = If(Vf)という関数で表し、電源とLEDの内部抵抗をゼロとして考えると、回路全体の電圧のバランスは以下のようになる。

(2)   \begin{equation*} E = V_f + RI = V_f + R I_f(V_f) \end{equation*}

これをIfについて解くと以下のようになる。

(3)   \begin{equation*} R = \dfrac{E - V_f}{I_f(V_f)} \end{equation*}

IfがVfの関数になっているのでややこしいが、一般にはデータシートの典型値などをそのまま用いて計算する例が多い。たとえば電源電圧が3.3Vで赤色LEDを発光させる場合、典型値としてIfTYP=20mAの時にVfTYP=2Vという値が示されているとすると保護抵抗値は以下のようになる。

(4)   \begin{equation*} R = \dfrac{3.3 - 2}{0.02} = 65 \Omega \end{equation*}

よく見かける保護抵抗値は100Ωとか330Ωといった値だが、こういう場合のVfやIfがどのようになるか、また順電流を10mAや30mAにしたい場合抵抗値をどうするかといったことを知りたい場合は非線形な方程式を解かなければならない。

特性曲線にの読み取りによる計算

LEDの特性が先に示したような特性曲線のように与えられている場合、電源電圧3.3Vに対して順電流をIf = 10mAとしたい場合は、グラフからVf =2.4V程度となるので、保護抵抗値は以下のように求められる。

(5)   \begin{equation*} R = \dfrac{3.3 - 2.4}{0.01} = 90 \Omega \end{equation*}

順電流の絶対最大定格値が30mAの場合、これを越えないようにするための最低の保護抵抗値はどうなるか。先の特性曲線からIf = 30mAに対してVf = 2.6V程度と読み取れるので、以下のように計算される。

(6)   \begin{equation*} R = \dfrac{3.3 - 2.6}{0.03} \fallingdotseq 23.33 \Omega \end{equation*}

市販のLEDのデータ

市販のLEDのデータシートの値の例は以下のようになっていた。なおA社のデータシートによると、より長期間使用するために順電流値を10～30mAの間で使用することが推奨されている。

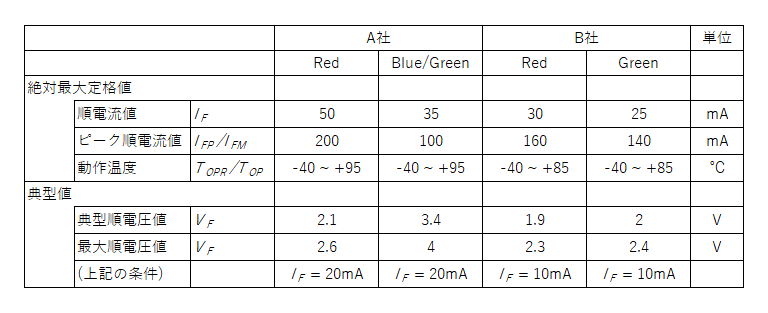
これらのLEDを典型値で用いる場合の保護抵抗値を計算してみる。A社の赤、青・緑のLEDを5Vで使う場合、

(7)   \begin{equation*} \left\{ \begin{align} \dfrac{5 - 2.1}{0.02} &= 145 \Omega \\ \dfrac{5 - 3.4}{0.02} &= 80 \Omega \end{align} \end{equation*}

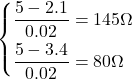
またB社の赤、緑のLEDを3.3Vで使う場合、

(8)   \begin{equation*} \left\{ \begin{align} \dfrac{3.3 - 1.9}{0.01} &= 140 \Omega \\ \dfrac{3.3 - 2}{0.01} &= 130 \Omega \end{align} \end{equation*}

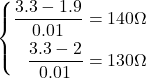
なお各LEDのIfとVfの関係をデータシートの特性曲線から典型値で読み取ってみると以下のようになり、概ね表の値に一致する。

  • A社の赤LED→20mAに対して約2.13V
  • A社の緑・青LED→20mAに対して約3.4V
  • B社の赤LED→10mAに対して1.9V

不明LEDの特性曲線

Raspberry Pi用のキットにはパーツのデータシートや型番などがなく、LEDの特性も分からない。そこで、抵抗値を取り換えながらVfやVrを計測し、Ifの計算値をプロットしてみた。
データシートで見られるカーブの形をしており、赤・緑・黄色の特性が近く、青と白はより大きなVfを必要としている。

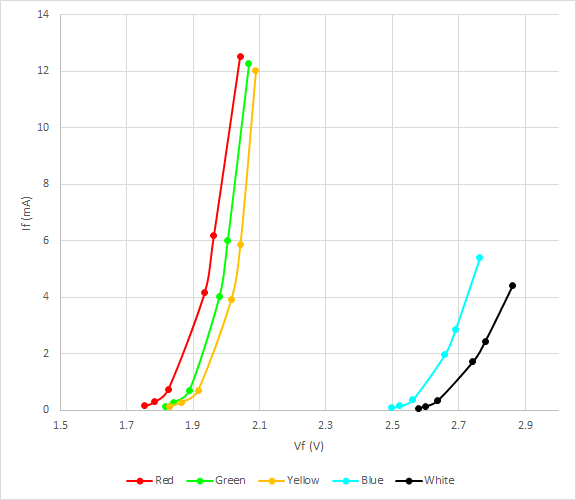
特性曲線は指数関数で近似できるので、片対数軸で表示してみる。若干指数関数よりもVfに対するIfの増加率が緩やかな傾向がある。

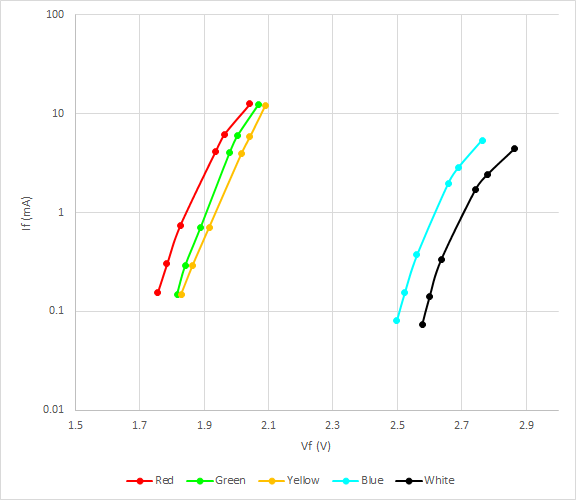
Excelの分析ツールでも指数関数近似をしてくれるが、ここで以下の式形で回帰をしてみた。まず以下の式で回帰する。

(9)   \begin{equation*} I_f = a e^{b V_f} \end{equation*}

一般にはa(exp(b Vf) – 1)の形で示されているが、回帰計算のしやすさのために形を少し変えている。両辺の対数をとって線形回帰する。

(10)   \begin{equation*} \ln I_f = \ln a + b V_f \end{equation*}

結果は分析ツールのグラフと同じ形で以下のようになる。

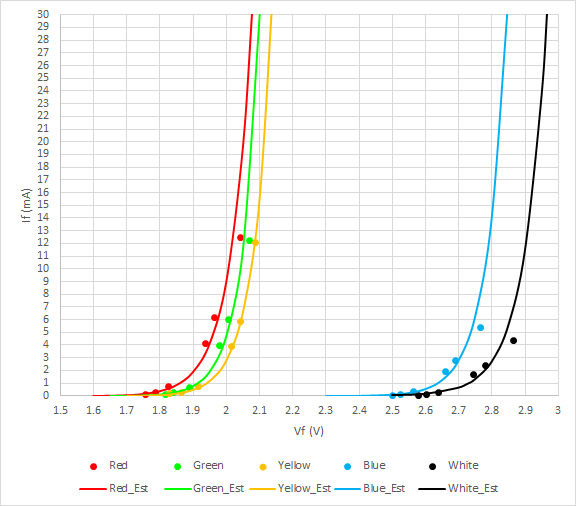
片対数で表すと以下のようになる。

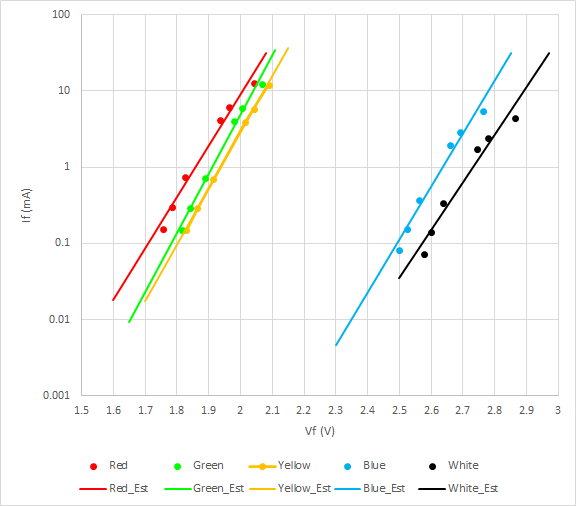
対数軸で線形性が良好な緑と黄は元の関数形でもよく一致しているが、赤と青・白についてはVfが大きいところでの乖離が大きくなる。ただしVfに対してIfが小さく推定されるため、たまたまとはいえ安全側になっている。

各色のLEDに対する推定式の定数は以下のようになった。

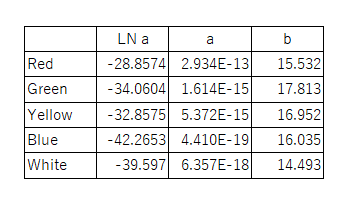
対数化した線形式での相関係数は0.978～0.999程度であり、かなり高い。土質・地質工学や水理学のように自然現象を扱う場合とは異なる。

なお、Ifを希望する値にするための抵抗値は以下のように計算できる。

(11)   \begin{equation*} I_f = a \exp{b V_f} = a \exp{b (E - R I_f)} \end{equation*}

この式をRについて解いて、

(12)   \begin{equation*} R = \dfrac{E - \dfrac{1}{b} \ln \dfrac{I_f}{a}}{I_f} \end{equation*}

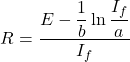
Ifを変化させた場合、各色のLEDに使う保護抵抗値は以下のように計算される。

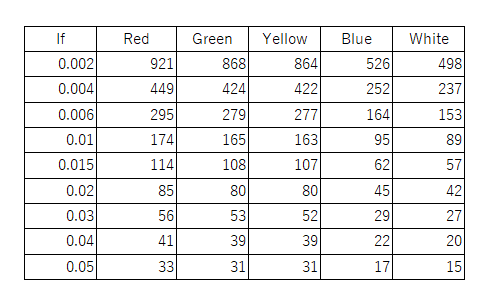
キットのテキストでは220Ωの抵抗をよく用いているが、その場合は赤・緑・黄色が7～8mA程度、青と白では4mA程度ということになる。実際、青と白のLEDは少し暗めかなというくらいの明るさなので、これらの計算結果は腹落ちできる。

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です