三角関数 – 加法定理

/ tau / コメントする

加法定理の一覧

(1)   \begin{eqnarray*} \sin ( \alpha \pm \beta) &=& \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos ( \alpha \pm \beta ) &=& \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \end{eqnarray*}

導出

第1ステップ – 等式の一つを導出

まず、以下のような図を考える。

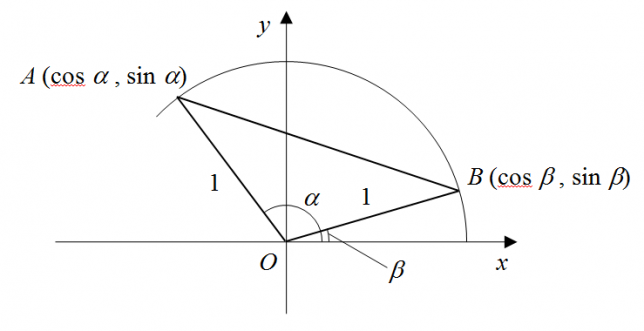
math_trigonometry_additiontheorem_1

ABの長さを余弦定理で表す。

(2)   \begin{equation*} ( \cos \alpha - \cos \beta )^2 + ( \sin \alpha - \sin \beta )^2 = 1^2 + 1^2 - 2 \cos (\alpha - \beta) \end{equation*}

これより以下を得るが、これは加法定理のうちの一つに対応している。

(3)   \begin{equation*} \cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{equation*}

なお上式は、cosの性質からαとβの大小関係に関わらず成り立つ。

第2ステップ – 符号の反転

式(3)でβ → – βと置くと以下を得る。

(4)   \begin{equation*} \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{equation*}

第3、4ステップ – cosからsinへの変換と符号の反転

式(3)でα → α+π/2と置くと以下を得る。

(5)   \begin{eqnarray*} \cos \left( \alpha + \frac{\pi}{2} - \beta \right) &=& \cos \left( \alpha + \frac{\pi}{2} \right) \cos \beta - \sin \left( \alpha + \frac{\pi}{2} \right) \sin \beta \\ - \sin ( \alpha - \beta ) &=& - \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \sin ( \alpha - \beta ) &=& \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{eqnarray*}

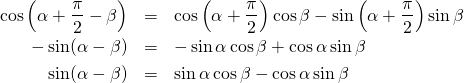
また上式においてβ → – βと置くと以下を得る。

(6)   \begin{eqnarray*} \sin ( \alpha + \beta ) &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{eqnarray*}

これで加法定理に関する4つの式が得られた。

一般角への拡張

αやβが第3象限、第4象限にあるときは、それらからπ/2、πを減じて冒頭の図に対応させ、式変形をすることで同じ解を得る。

例えば下図のように、αが第3象限、βが第1象限にあるケースを考える。

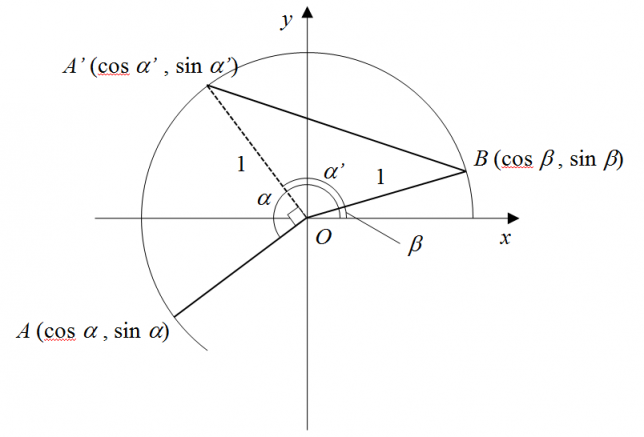
math_trigonometry_additiontheorem_2

ここでα = α’ + π/2と置けば、α’について加法定理が成り立つことが分かっているので、

(7)   \begin{eqnarray*} \sin ( \alpha ' \pm \beta) &=& \sin \alpha ' \cos \beta \pm \cos \alpha ' \sin \beta \\ \cos ( \alpha ' \pm \beta ) &=& \cos \alpha ' \cos \beta \mp \sin \alpha ' \sin \beta \end{eqnarray*}

αとα’の関係より、

(8)   \begin{eqnarray*} \sin \left( \alpha - \frac{\pi}{2} \pm \beta \right) &=& \sin \left( \alpha - \frac{\pi}{2} \right) \cos \beta \pm \cos \left( \alpha - \frac{\pi}{2} \right) \sin \beta \\ \cos \left( \alpha - \frac{\pi}{2} \pm \beta \right) &=& \cos \left( \alpha - \frac{\pi}{2} \right) \cos \beta \mp \sin \left( \alpha - \frac{\pi}{2} \right) \sin \beta \end{eqnarray*}

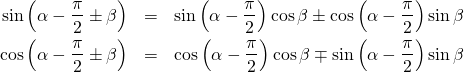
これらより、以下の下方定理がこのケースについて成り立つことが示される。

(9)   \begin{eqnarray*} - \cos ( \alpha \pm \beta) &=& - \cos \alpha \cos \beta \pm \sin \alpha \sin \beta \\ \sin ( \alpha \pm \beta ) &=& \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \end{eqnarray*}

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です