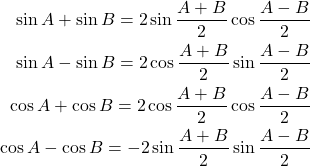三角関数の積和の公式は、通常以下の様に表される。
(1) 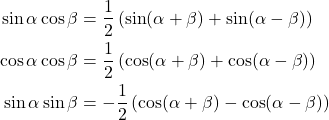
これらの式は、加法定理の式を足し引きすることで得られる。cos α sin βについても計算できるが、上の第1式と同じになる。
(2) 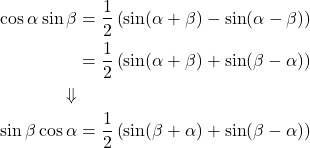
α + β = A, α − β = Bと置いて、以下の式を得る。
(3) 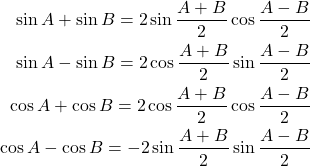
三角関数の積和の公式は、通常以下の様に表される。
(1) 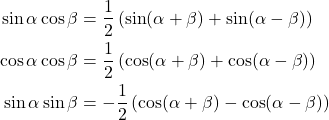
これらの式は、加法定理の式を足し引きすることで得られる。cos α sin βについても計算できるが、上の第1式と同じになる。
(2) 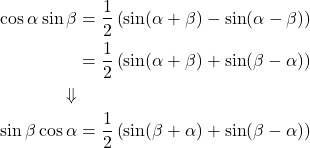
α + β = A, α − β = Bと置いて、以下の式を得る。
(3)