三角関数 – 2つの三角関数の和

概要

以下の関係を確認する。

(1) $\begin{equation*} A_1 \sin x + A_2 \cos x = A \sin (x + \alpha) = A \cos(x + \beta) \end{equation*}$

同じ変数のsineとcosineの和について考える。変数は同じだが、互いの係数が異なっている。

(2) $\begin{equation*} s = A_1 \sin x + A_2 \cos x \end{equation*}$

ここで以下のような変数を導入する。

(3) $\begin{equation*} A = \sqrt {A_1^2 + A_2^2} \end{equation*}$

これによって式(2)を以下の様に変形する。

(4) $\begin{equation*} s = A \left( \frac{A_1}{A} \sin x + \frac{A_2}{A} \cos x \right) \end{equation*}$

ここで、以下の様に係数を再定義する。

(5) $\begin{align*} \frac{A_1}{A} = \cos \alpha \\ \frac{A_2}{A} = \sin \alpha \end{align*}$

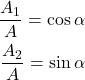
これに加法定理を考慮して以下の様に単一の正弦関数になる。

(6) $\begin{align*} s &= A ( \sin x \cos \alpha + \cos x \sin \alpha) \\ &= A \sin (x + \alpha) \end{align*}$

また、係数を以下の様に再定義する。

(7) $\begin{align*} \frac{A_1}{A} = \sin \beta \\ \frac{A_2}{A} = \cos \beta \end{align*}$

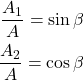
この場合は結果が余弦関数となる。同じ変数のsineとcosineは位相が違うだけなので、結果としては当然。

(8) $\begin{align*} s &= A ( \sin x \sin \beta + \cos x \cos \beta) \\ &= A \cos (x - \beta) \end{align*}$