前後の判定
ある点が運動しているとき、着目する他の点が進行方向の前方にあるのか、後方にあるのかを判定したい時があるが、2次元の場合は、ベクトルの内積を使うとこの判定が簡単にできる。
以下の図で、点sがvの方向に進んでいるとき、点pが前方/後方のいずれにあるかを判定する。
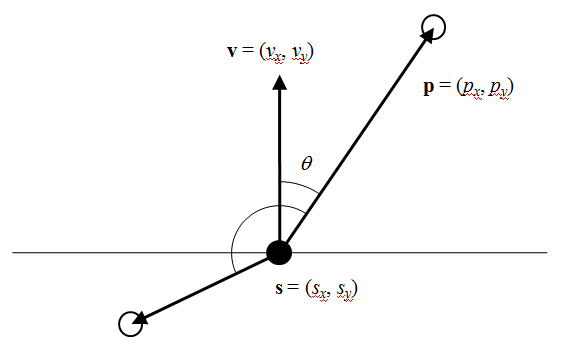
sを起点としたベクトルvと、sから見たpの相対的な位置ベクトルの内積を考えると、
![]()
上式で0≤θ≤90度の範囲であればpはsの前方にあり、このときcosθ≥0。また90度<θ≤180度の範囲ならpはsの後方にあり、cosθ<0となる。
内積を計算する角は、ベクトルvとpのなす角なので、pがsの左右どちらにあるかは問わない。
以上のことから、進行方向のベクトルvと、自身から見た相対的な着目点の位置ベクトルの内積が正なら着目点は前方に、負なら後方にあることになる(ゼロならば真横)。
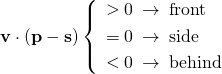
左右の判定
方向ベクトルvを90度回転させた上で上記の前後判定を行うことで左右判定が可能になる。
右へ回転させたベクトルに対して前方なら元の方向ベクトルの右、後方なら元の方向ベクトルの左と判定できる。