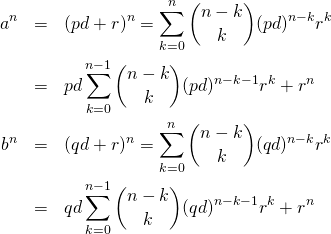商と剰余
剰余(余り)について
![]() の商が
の商が![]() 、余りが
、余りが![]() のとき、以下のように表される。d:divisor、q:quotient、r:reminderの意味。
のとき、以下のように表される。d:divisor、q:quotient、r:reminderの意味。
(1) ![]()
余りの定義を「割る数未満の自然数あるいは0」とすると、
(2) 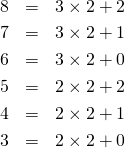
割られる数が負の場合には、
(3) 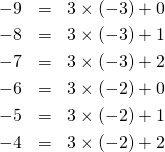
割る数が負の場合には、
(4) 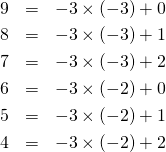
負数の余り
余りとして負の数を認めることもできる。ただしその場合、商と余りの組み合わせが1つとは限らない。
(5) ![]()
余りの定義(要件)は以下の2通りがあり、いずれを採用するかは任意。
- 余りを割る数の絶対値より小さい0以上とする
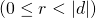
- 余りの絶対値が割る数の絶対値より小さい数とする
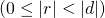
特別な場合の余り
割る数が1あるいは-1のときは、余りは常に0。
(6) ![]()
割られる数が1のときの余りは1、割られる数が-1なら余りは割る数の絶対値から1を現じた値(余りを正と定義した場合)。
(7) 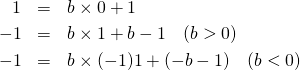
合同式
合同式の定義
整数![]() を正の整数
を正の整数![]() で割った余りが等しいとき、以下のように表記し、「
で割った余りが等しいとき、以下のように表記し、「![]() は
は![]() を法として合同である」という。
を法として合同である」という。
(8) ![]()
これは次のようにも表現できる。
(9) ![]()
合同式の例
(10) 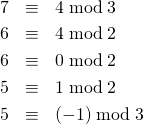
角度の例
以下の例では、330度と−30度が合同となっている。360度回転するたびに元の位置に戻るイメージ。
(11) 
合同式の性質
以下、合同式の![]() を省略する。
を省略する。
合同式の和
(12) ![]()
【証明】
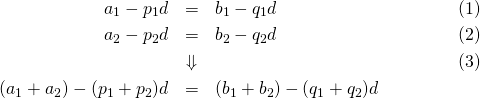
合同式の積
(13) ![]()
【証明】
(14) 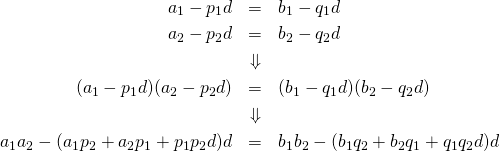
合同式の商
![]() が互いに素
が互いに素![]() のとき、以下が成り立つ。
のとき、以下が成り立つ。
(15) ![]()
【証明】
(16) ![]()
ここで![]() は互いに素なので、
は互いに素なので、![]() が
が![]() の倍数となる。
の倍数となる。
(17) ![]()
合同式の冪乗
(18) ![]()
【証明】
(19) ![]()
(20)