PCA – 次元削減と逆変換について

1 概要
2 簡単な例
- 2.1 全主成分を使った手順
- 2.2 最初から主成分を限定する手順
  - 2.2.1 概要
3 まとめ

概要

主成分分析(PCA)において、次元削減により主成分の一部だけを残し、それを逆変換することを考える。

結論から言うと、以下の2つの操作は同じ結果をもたらす。

全ての主成分を用いて変換し、削減する主成分に対応する元の特徴量を0とし、逆変換する
削減する主成分より低次の主成分のみで変換し、それを逆変換する

簡単な例

全主成分を使った手順

概要

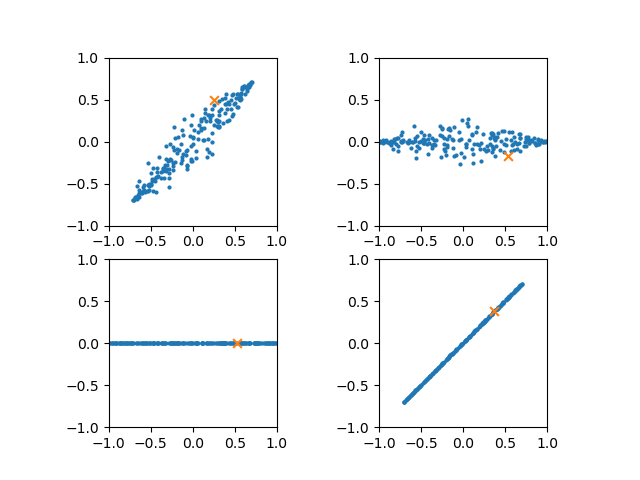
最初の例は、2次元のデータについて以下のような操作を行っている。

2つの主成分まで使ってデータを変換
第2主成分に対応する変換後のデータを0にする
そのデータを逆変換する

元データの作成

まず元データを作成し、左上に散布図を描画。

元データは水平線にcosine状に正規分布するノイズを乗せ、それを45度回転させている。

また、適当な位置に特定の点を1つ定義している。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

np.random.seed(0)

n_data = 200
cs = 1 / np.sqrt(2)
x = np.linspace(-1, 1, n_data)
y = np.random.randn(n_data) * np.cos(x * np.pi / 2) / 6
x, y = cs * x - cs * y, cs * x + cs * y
xp, yp = 0.25, 0.5

X = np.array([x, y]).reshape(-1, 2)
Xp = np.array([xp, yp]).reshape(-1, 2)

fig1, axes1 = plt.subplots(2, 2) &nbsp;axes1[0, 0].scatter(X[:, 0], X[:, 1], marker='o', s=4)
axes1[0, 0].scatter(Xp[0, 0], Xp[0, 1], marker='x', s=40)

print("Xp original:{}".format(Xp))
# Xp original:[[0.25 0.5 ]]

.....

for axis in axes1.ravel():
    axis.set_aspect('equal')
    axis.set_xlim(-1, 1)
    axis.set_ylim(-1, 1)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.decomposition import PCA

np.random.seed(0)

n_data = 200

cs = 1 / np.sqrt(2)

x = np.linspace(-1, 1, n_data)

y = np.random.randn(n_data) * np.cos(x * np.pi / 2) / 6

x, y = cs * x - cs * y, cs * x + cs * y

xp, yp = 0.25, 0.5

X = np.array([x, y]).reshape(-1, 2)

Xp = np.array([xp, yp]).reshape(-1, 2)

fig1, axes1 = plt.subplots(2, 2)  axes1[0, 0].scatter(X[:, 0], X[:, 1], marker='o', s=4)

axes1[0, 0].scatter(Xp[0, 0], Xp[0, 1], marker='x', s=40)

print("Xp original:{}".format(Xp))

# Xp original:[[0.25 0.5 ]]

.....

for axis in axes1.ravel():

axis.set_aspect('equal')

axis.set_xlim(-1, 1)

axis.set_ylim(-1, 1)

plt.show()

フィッティングと元データの変換

次に元データをPCAによって変換し、変換後の散布図を右上に描画。

斜めだった分布が、第1主成分がx軸と重るように変換されて水平になる。

.....

pca = PCA().fit(X)
X_trans = pca.transform(X)
Xp_trans = pca.transform(Xp)

axes1[0, 1].scatter(X_trans[:, 0], X_trans[:, 1], marker='o', s=4)
axes1[0, 1].scatter(Xp_trans[0, 0], Xp_trans[0, 1], marker='x', s=40)

print("Xp transfomed:{}".format(Xp_trans))
# Xp transfomed:[[ 0.53055026 -0.17107022]]

.....

.....

pca = PCA().fit(X)

X_trans = pca.transform(X)

Xp_trans = pca.transform(Xp)

axes1[0, 1].scatter(X_trans[:, 0], X_trans[:, 1], marker='o', s=4)

axes1[0, 1].scatter(Xp_trans[0, 0], Xp_trans[0, 1], marker='x', s=40)

print("Xp transfomed:{}".format(Xp_trans))

# Xp transfomed:[[ 0.53055026 -0.17107022]]

.....

第2主成分のデータの削除

変換後のデータにおいて、第2主成分に関する値を0とし、左下に散布図を描画。

第2成分に相当する垂直成分が0になる。

.....

X_trans[:, 1] = 0
Xp_trans[0, 1] = 0
axes1[1, 0].scatter(X_trans[:, 0], X_trans[:, 1], marker='o', s=4)
axes1[1, 0].scatter(Xp_trans[0, 0], Xp_trans[0, 1], marker='x', s=40)

.....

.....

X_trans[:, 1] = 0

Xp_trans[0, 1] = 0

axes1[1, 0].scatter(X_trans[:, 0], X_trans[:, 1], marker='o', s=4)

axes1[1, 0].scatter(Xp_trans[0, 0], Xp_trans[0, 1], marker='x', s=40)

.....

逆変換

第2主成分を0としたデータを逆変換して描画。

第1主成分に直角な第2主成分が0となり、全点が一直線上に並ぶ。

X_inv = pca.inverse_transform(X_trans)
Xp_inv = pca.inverse_transform(Xp_trans)
axes1[1, 1].scatter(X_inv[:, 0], X_inv[:, 1], marker='o', s=4)
axes1[1, 1].scatter(Xp_inv[0, 0], Xp_inv[0, 1], marker='x', s=40)

print("Xp inversed:{}".format(Xp_inv))
# Xp inversed:[[0.37112019 0.37919056]]

.....

X_inv = pca.inverse_transform(X_trans)

Xp_inv = pca.inverse_transform(Xp_trans)

axes1[1, 1].scatter(X_inv[:, 0], X_inv[:, 1], marker='o', s=4)

axes1[1, 1].scatter(Xp_inv[0, 0], Xp_inv[0, 1], marker='x', s=40)

print("Xp inversed:{}".format(Xp_inv))

# Xp inversed:[[0.37112019 0.37919056]]

.....

最初から主成分を限定する手順

概要

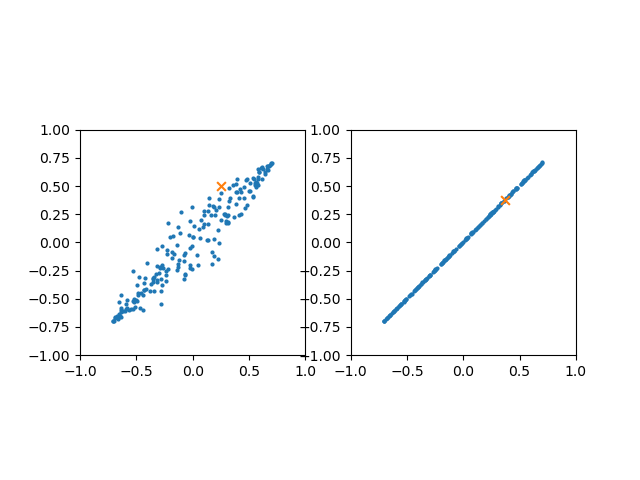
次の例は元の特徴量を操作せず、以下のような手順に寄っている。

PCAのモデル生成時に、n_component=1とする
そのPCAモデルで元データを変換する
変換したデータを逆変換する

fig2, axes2 = plt.subplots(1, 2)

axes2[0].scatter(X[:, 0], X[:, 1], marker='o', s=4)
axes2[0].scatter(Xp[0, 0], Xp[0, 1], marker='x', s=40)

print("Xp original:{}".format(Xp))
# Xp original:[[0.25 0.5 ]]

pca = PCA(n_components=1).fit(X)
X_trans = pca.transform(X)
Xp_trans = pca.transform(Xp)

print("Xp transfomed:{}".format(Xp_trans))
# Xp transfomed:[[0.53055026]]

X_inv = pca.inverse_transform(X_trans)
Xp_inv = pca.inverse_transform(Xp_trans)
axes2[1].scatter(X_inv[:, 0], X_inv[:, 1], marker='o', s=4)
axes2[1].scatter(Xp_inv[0, 0], Xp_inv[0, 1], marker='x', s=40)

print("Xp inversed:{}".format(Xp_inv))
# Xp inversed:[[0.37112019 0.37919056]]

for axis in axes2.ravel():
    axis.set_aspect('equal')
    axis.set_xlim(-1, 1)
    axis.set_ylim(-1, 1)

plt.show()

fig2, axes2 = plt.subplots(1, 2)

axes2[0].scatter(X[:, 0], X[:, 1], marker='o', s=4)

axes2[0].scatter(Xp[0, 0], Xp[0, 1], marker='x', s=40)

print("Xp original:{}".format(Xp))

# Xp original:[[0.25 0.5 ]]

pca = PCA(n_components=1).fit(X)

X_trans = pca.transform(X)

Xp_trans = pca.transform(Xp)

print("Xp transfomed:{}".format(Xp_trans))

# Xp transfomed:[[0.53055026]]

X_inv = pca.inverse_transform(X_trans)

Xp_inv = pca.inverse_transform(Xp_trans)

axes2[1].scatter(X_inv[:, 0], X_inv[:, 1], marker='o', s=4)

axes2[1].scatter(Xp_inv[0, 0], Xp_inv[0, 1], marker='x', s=40)

print("Xp inversed:{}".format(Xp_inv))

# Xp inversed:[[0.37112019 0.37919056]]

for axis in axes2.ravel():

axis.set_aspect('equal')

axis.set_xlim(-1, 1)

axis.set_ylim(-1, 1)

plt.show()

まとめ

途中で表示させているXpのデータが、2つの手順で全く同じであることがわかる。

最初から主成分を限定することで、元の特徴量を意識せずに次元削減ができる。

TauStation

PCA – 次元削減と逆変換について

概要

簡単な例

全主成分を使った手順

概要

元データの作成

フィッティングと元データの変換

第2主成分のデータの削除

逆変換

最初から主成分を限定する手順

概要

まとめ

コメントを残すコメントをキャンセル

概要

簡単な例

全主成分を使った手順

概要

元データの作成

フィッティングと元データの変換

第2主成分のデータの削除

逆変換

最初から主成分を限定する手順

概要

まとめ

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル