単振動の微分方程式の解

概要

以下の単振動に関する方程式の解法を整理した。

(1) $\begin{equation*} \frac{d^2x(t)}{dt^2} + \omega^2 x(t) = 0 \quad \left( t = 0 \Rightarrow \left\{ \begin{array}{l} x = X_0 \\ \dot{x} = 0 \end{array} \right) \end{equation*}$

変数変換による方法

式(1)の両辺にdx/dtを掛けて変形する。

(2) $\begin{align*} &\frac{dx}{dt} \frac{d^2x}{dt^2} + \omega^2 x \frac{dx}{dt} = 0 \\ &\frac{1}{2} \frac{d}{dt} \left( \frac{dx}{dt} \right)^2 + \frac{1}{2} \omega^2 \frac{d}{dt} \left( x^2 \right) = 0 \end{align*}$

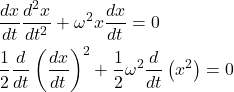
これをtで積分して以下を得る。

(3) $\begin{equation*} \left( \frac{dx}{dt} \right)^2 + \omega^2 x^2 = C \end{equation*}$

ここでC = ω²A²とおいて

(4) $\begin{equation*} \frac{dx}{dt} \right = \pm \omega \sqrt {A^2 - x^2} \quad (x \le A) \end{equation*}$

さらにx = A cos θとおいて、

(5) $\begin{equation*} (- A \sin \theta) \frac{d \theta}{dt} = \pm \omega A \sin \theta \quad \Rightarrow \quad \frac{d \theta}{dt} = \mp \omega A \end{equation*}$

θの解は以下の様になる。

(6) $\begin{equation*} \theta = \mp \omega t + \alpha \end{equation*}$

x = A cos θだったので、以下を得る。

(7) $\begin{equation*} x = A \cos (\omega t + \alpha) \end{equation*}$

初期条件から

(8) $\begin{align*} x|_{t=0} &= A \cos (\alpha) = X0 \\ \dot{x}|_{t=0} &= -A \sin (\alpha) = 0 \end{align*}$

これより以下の解を得る。

(9) $\begin{equation*} x = X_0 \cos \omega t \end{equation*}$

オイラーの公式を使う方法

式(1)の解を以下の様に置く。

(10) $\begin{equation*} x = e^{\lambda t} \end{equation*}$

これを式(1)に代入して

(11) $\begin{equation*} \lambda^2 e^{\lambda t} + \omega^2 e^{\lambda t} = 0 \quad \Rightarrow \quad \lambda ^2 + \omega^2 = 0 \quad \Rightarrow \quad \lambda = \pm i \omega \end{equation*}$

この解を式(10)に代入して2つの関数が得られるが、式(1)の一般解はこれらの線形結合として得られる。

(12) $\begin{equation*} x = A e^{i \omega t} + Be^{-i \omega t} \end{equation*}$

ここで以下のオイラーの公式を適用する。

(13) $\begin{equation*} e^{\pm i \theta} = \cos \theta \pm i \sin \theta \end{equation*}$

これにより式(12)は以下のように書ける。

(14) $\begin{align*} x &= C_1 (\cos \omega t + i \sin \omega t) + C_2 (\cos \omega t - i \sin \omega t) \\ &= (C_1 + C_2) \cos \omega t + (C_1 - C_2) i \sin \omega t \end{align*}$

xが実数解を持つために、cos, sin双方の係数が実数となるよう、複素係数C₁, C₂を以下の様に置く。

(15) $\begin{align*} C_1 = \frac{A_1 + i A_2}{2} \\ C_2 = \frac{A_1 - i A_2}{2} \end{align*}$

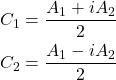
これにより、式(16)は以下の様に変形される。

(16) $\begin{equation*} x = A_1 \cos \omega t + A_2 \sin \omega t \end{equation*}$

三角関数の和の関係から、上式は以下の様に表せる。

(17) $\begin{equation*} x = A \cos (\omega t + \alpha) \end{equation*}$

初期条件(8)より式(9)と同じ解を得る。

TauStation

単振動の微分方程式の解

概要

変数変換による方法

オイラーの公式を使う方法

コメントを残すコメントをキャンセル

概要

変数変換による方法

オイラーの公式を使う方法

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル