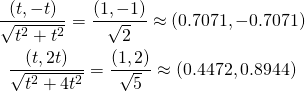タグ: 代数

行列の固有値・固有ベクトル

/ tau / コメントする

概要

行列{\rm A}の固有値・固有ベクトルは以下で定義される。

(1)   \begin{equation*} \boldsymbol{Ax} = \lambda \boldsymbol{x} \end{equation*}

これを以下のように変形する。

(2)   \begin{equation*} (\boldsymbol{A} - \lambda \boldsymbol{I} ) \boldsymbol{x} = {\bf 0} \end{equation*}

この方程式が解をもつためには、以下の条件が必要。

(3)   \begin{equation*} | \boldsymbol{A} - \lambda \boldsymbol{I} | = 0 \end{equation*}

例題

以下の行列に対する固有値、固有ベクトルを求める。

(4)   \begin{equation*} \boldsymbol{A} = \left( \begin{array}{cc} 3 & 1 \\ 2 & 4 \end{array} \right) \end{equation*}

この行列に対する固有値方程式は以下の通り。

(5)   \begin{equation*} | \boldsymbol{A} - \lambda \boldsymbol{I} | = \left| \left( \begin{array}{cc} 3 & 1 \\ 2 & 4 \end{array} \right) - \lambda \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \right| = \left| \begin{array}{cc} 3 - \lambda & 1 \\ 2 & 4 - \lambda \end{array} \right| = 0 \end{equation*}

これを解くと、

(6)   \begin{align*} & (3 - \lambda) (4 - \lambda) - 2 = 0 \\ & \lambda ^2 - 7 \lambda + 10 = 0 \\ & (\lambda - 2)(\lambda - 5) = 0 \\ & \lambda = 2, \; 5 \end{align*}

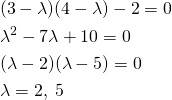
次に、各固有値に対する固有ベクトルを求める。

まず\lambda = 2に対しては、

(7)   \begin{gather*} \left( \begin{array}{cc} 3 - 2 & 1 \\ 2 & 4 - 2 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{cc} 1 & 1 \\ 2 & 2 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \end{array} \right) \\ \Rightarrow \; y = -x \\ \therefore \; \boldsymbol{x} = (t, -t) \end{gather*}

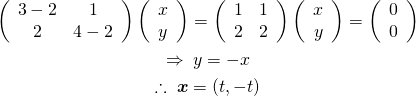
確認してみると、

(8)   \begin{gather*} \boldsymbol{Ax} = \left( \begin{array}{cc} 3 & 1 \\ 2 & 4 \end{array} \right) \left( \begin{array}{c} t \\ -t \end{array} \right) = \left( \begin{array}{c} 2t \\ -2t \end{array} \right) , \quad \lambda \boldsymbol{x} = 2 \left( \begin{array}{c} t \\ -t \end{array} \right) = \left( \begin{array}{c} 2t \\ -2t \end{array} \right) \end{gather*}

また\lambda = 5に対しては、

(9)   \begin{gather*} \left( \begin{array}{cc} 3 - 5 & 1 \\ 2 & 4 - 5 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{cc} -2 & 1 \\ 2 & -1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \end{array} \right) \\ \Rightarrow \; y = 2x \\ \therefore \; \boldsymbol{x} = (t, 2t) \end{gather*}

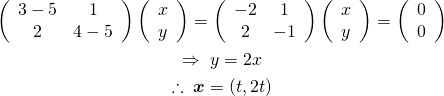
こちらも確認してみると、

(10)   \begin{gather*} \boldsymbol{Ax} = \left( \begin{array}{cc} 3 & 1 \\ 2 & 4 \end{array} \right) \left( \begin{array}{c} t \\ 2t \end{array} \right) = \left( \begin{array}{c} 5t \\ 10t \end{array} \right) , \quad \lambda \boldsymbol{x} = 5 \left( \begin{array}{c} t \\ 2t \end{array} \right) = \left( \begin{array}{c} 5t \\ 10t \end{array} \right) \end{gather*}

なお、固有ベクトルを数値で表現する際、ノルムが1となるように正規化することが多い。

(11)   \begin{gather*} \boldsymbol{x} \rightarrow \frac{\boldsymbol{x}}{\| {\boldsymbol{x}} \|} \end{gather*}

上の例で固有値ベクトルを正規化すると以下の通り。

(12)   \begin{gather*} \frac{(t, -t)}{\sqrt{t^2 + t^2}} = \frac{(1, -1)}{\sqrt{2}} \approx (0.7071, -0.7071) \\ \frac{(t, 2t)}{\sqrt{t^2 + 4t^2}} = \frac{(1, 2)}{\sqrt{5}} \approx (0.4472, 0.8944) \end{gather*}