ベクトルと行列の定義
リテラル
ベクトルはnp.array()で引数にリストを指定して定義。
|
1 2 3 4 |
v = np.array([1, 2, 3]) print(v) # [1 2 3] |
行列は同じくnp.array()で引数に二次元配列のリストを指定して定義。
|
1 2 3 4 5 |
m = np.array([[1, 2, 3], [4, 5, 6]]) print(m) # [[1 2 3] # [4 5 6]] |
単位行列
numpy.identity(n)でn×nの単位行列を生成。
|
1 2 3 4 5 6 |
print(np.identity(4)) # [[1. 0. 0. 0.] # [0. 1. 0. 0.] # [0. 0. 1. 0.] # [0. 0. 0. 1.]] |
転置
行列の転置にはtranspose()メソッドを使う。代替として.Tとしてもよい。
|
1 2 3 4 5 6 7 8 9 10 |
m = np.array([[1, 2, 3], [4, 5, 6]]) print(m.transpose()) print(m.T) # [[1 4] # [2 5] # [3 6]] # [[1 4] # [2 5] # [3 6]] |
一次元配列で定義したベクトルにはtranspose()は効かない。列ベクトルに変換するにはreshape()メソッドを使う(reshape(行数, 列数))。
|
1 2 3 4 5 6 7 8 |
v = np.array([1, 2, 3]) print(v.T) print(v.reshape(3, 1)) # [1 2 3] # [[1] # [2] # [3]] |
演算
定数倍
ベクトル・行列の定数倍は、各要素の定数倍。
|
1 2 3 4 5 6 7 8 9 10 |
a = 2 v = np.array([1, 2, 3]) m = np.array([[1, 2, 3], [4, 5, 6]]) print(a*v) print(a*m) # [2 4 6] # [[ 2 4 6] # [ 8 10 12]] |
加減
同じ要素数のベクトル、同じ次元の行列同士の下限は要素同士の加減
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
a = np.array([1, 2, 3]) b = np.array([2, 4, 6]) A = np.array([[1, 2], [3, 4]]) B = np.array([[2, 4], [6, 8]]) print(a + b) print(a - b) print(A + B) print(A - B) # [3 6 9] # [-1 -2 -3] # [[ 3 6] # [ 9 12]] # [[-1 -2] # [-3 -4]] |
ベクトルの内積
同じ要素数のベクトルの内積(ドット積)はnp.dot()で計算。
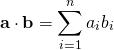
|
1 2 3 4 5 |
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) print(np.dot(a, b)) # 32 |
*演算子を使うと、要素ごとの積になる。
|
1 2 3 |
print(a*b) # [ 4 10 18] |
行列の積
行列同士の積もnp.dot()で計算。l×m行列とm×n行列の積はl×n行列になる。
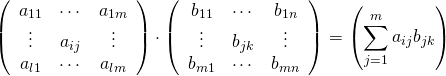
|
1 2 3 4 5 6 7 8 9 |
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4], [5, 6]]) print(np.dot(A, B)) # [[22 28] # [49 64]] |
次元数が整合しないとエラーになる。
|
1 2 3 4 5 6 7 |
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4]]) print(np.dot(A, B)) # ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0) |
行ベクトルと行列の積は、ベクトルを前からかけてok。
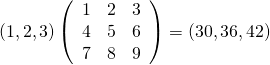
|
1 2 3 4 5 6 7 |
a = np.array([1, 2, 3]) A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(np.dot(a, A)) # [30 36 42] |
行列と列ベクトルの積は、一次元配列のベクトルをreshape()で列ベクトルに変換してから。
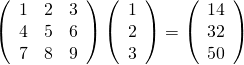
|
1 2 3 4 5 6 7 8 9 |
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) a = np.array([1, 2, 3]).reshape(3, 1) print(np.dot(A, a)) # [[14] # [32] # [50]] |
なお、np.dot()の代わりに演算子@が使える。ベクトル同士なら内積、少なくともいずれか一つが行列なら行列積。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
a = np.array([1, 2]) b = np.array([1, 2, 3]).reshape(3, 1) A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4], [5, 6]]) print(a @ a) print(a @ A) print(A @ b) print(A @ B) # 5 # [ 9 12 15] # [[14] # [32]] # [[22 28] # [49 64]] |
numpy.linalgパッケージ
行列式
行列式はnumpy.linalgパッケージのdet()関数で得られる。linalgは”linear algebra”の略で、慣例としてLAという名前で代替される。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy.linalg as LA A = np.array([[1, 2], [3, 4]]) B = np.array([[1, 2, 3], [2, 1, 3], [3, 1, 2]]) print(LA.det(A)) print(LA.det(B)) # -2.0000000000000004 # 6.000000000000001 |
逆行列
逆行列はnumpy.linalgパッケージのinv()関数で得られる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
A = np.array([[1, 2], [3, 4]]) B = np.array([[1, 2, 3], [2, 1, 3], [3, 1, 2]]) print(LA.inv(A)) print(LA.inv(B)) # [[-2. 1. ] # [ 1.5 -0.5]] # [[-0.16666667 -0.16666667 0.5 ] # [ 0.83333333 -1.16666667 0.5 ] # [-0.16666667 0.83333333 -0.5 ]] |
固有値・固有ベクトル
正方行列の固有値と固有ベクトルを、eig()関数で得ることができる(行列の固有値・固有ベクトルの例題を用いた)。
|
1 2 3 4 5 6 |
A = np.array([[3, 1], [2, 4]]) print(LA.eig(A)) # (array([2., 5.]), array([[-0.70710678, -0.4472136 ], # [ 0.70710678, -0.89442719]])) |
結果は固有値が並んだベクトルと固有ベクトルが並んだ配列で、それぞれを取り出して利用する。なお、固有ベクトルはノルムが1となるように正規化されている。
|
1 2 3 4 5 6 7 |
eigenvalues, eigenvectors = LA.eig(A) print(eigenvalues) print(eigenvectors) # [2. 5.] # [[-0.70710678 -0.4472136 ] # [ 0.70710678 -0.89442719]] |
注意が必要なのは固有ベクトルの方で、各固有ベクトルは配列の列ベクトルとして並んでいる。固有ベクトルを取り出す方法は2通り。
固有値に対応するサフィックスで列ベクトルを取り出す。この方法はnumpyの公式ドキュメントにも以下のように書かれている。
- v(…, M, M) array
- The normalized (unit “length”) eigenvectors, such that the column v[:,i] is the eigenvector corresponding to the eigenvalue w[i].
|
1 2 3 |
print(eigenvectors[:,0], eigenvectors[:,1]) # [-0.70710678 0.70710678] [-0.4472136 -0.89442719] |
固有ベクトルの配列を転置して、行ベクトルの並びにする。
|
1 2 3 4 |
eigenvectors = eigenvectors.T print(eigenvectors[0], eigenvectors[1]) # [-0.70710678 0.70710678] [-0.4472136 -0.89442719] |