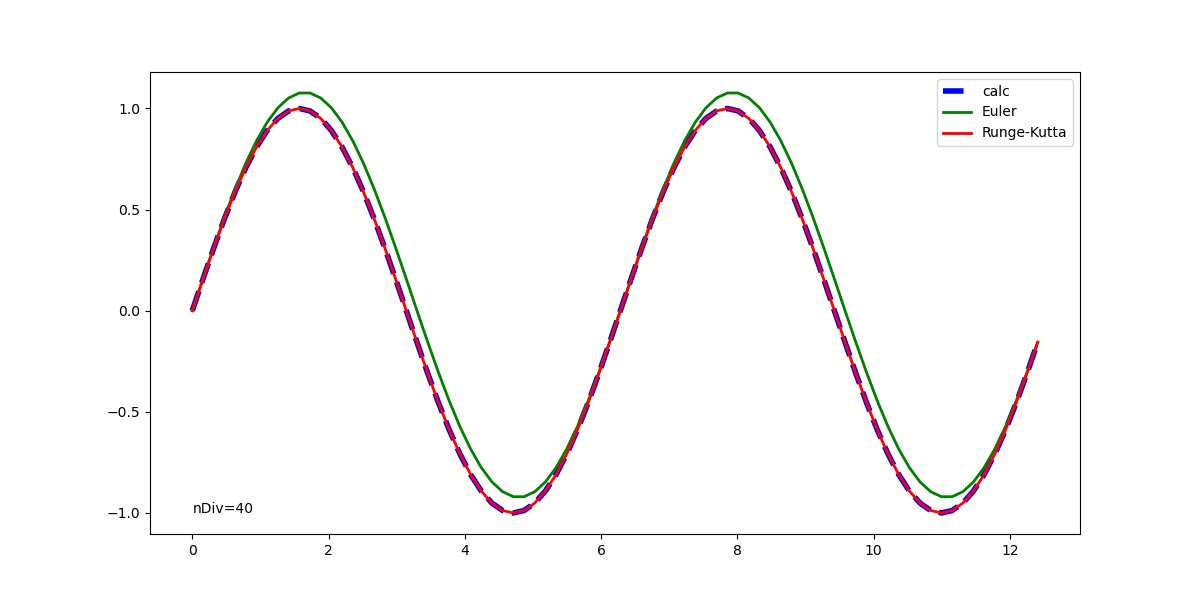
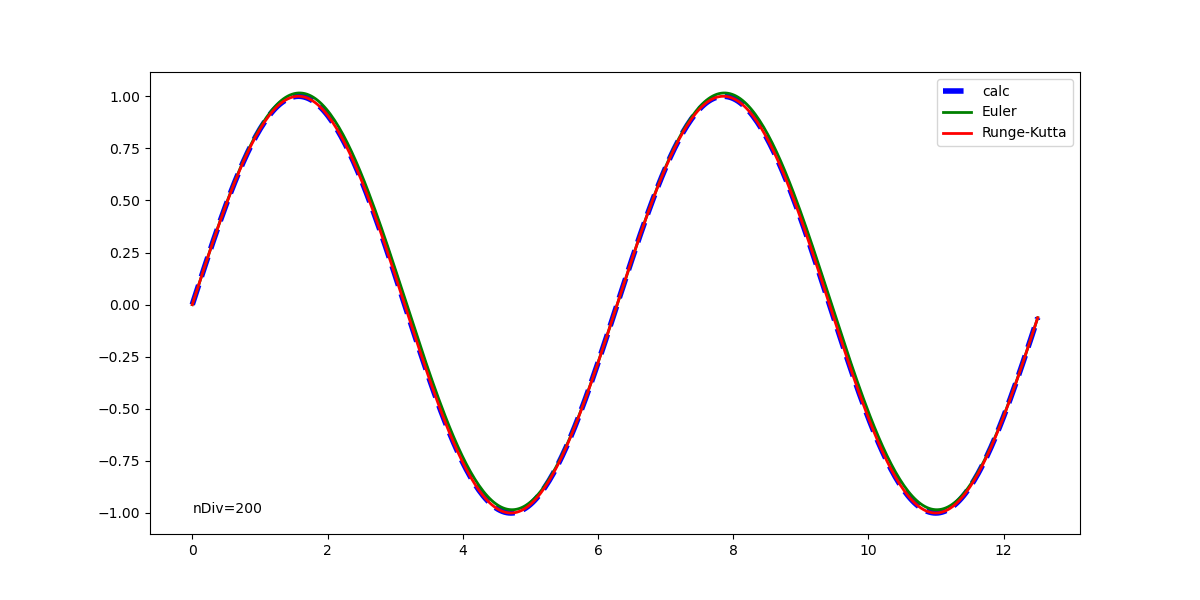
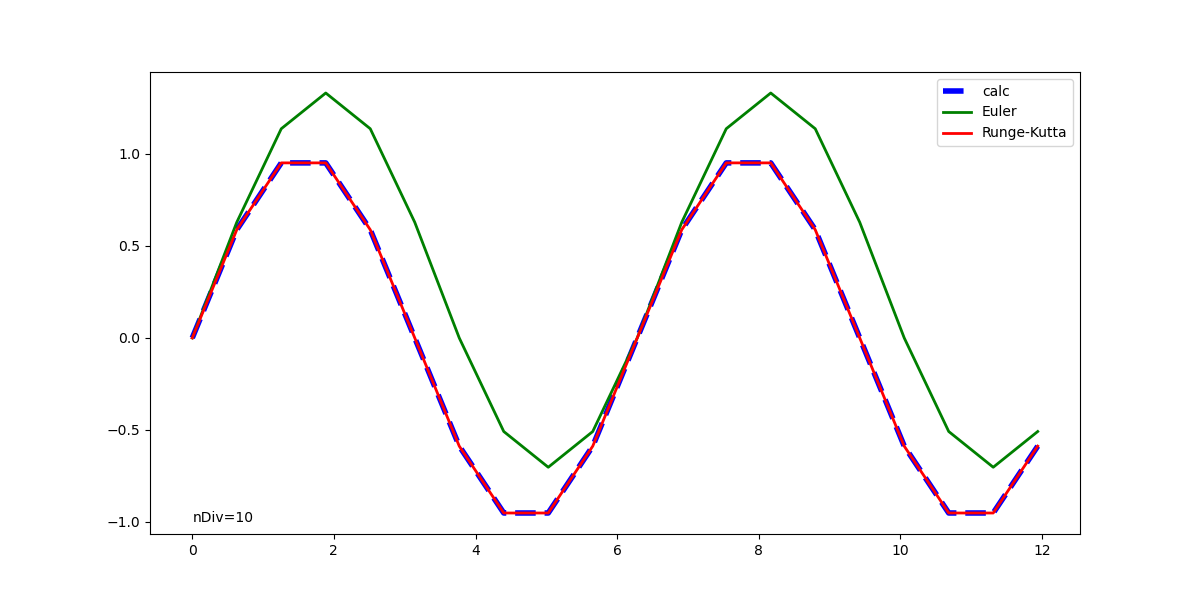
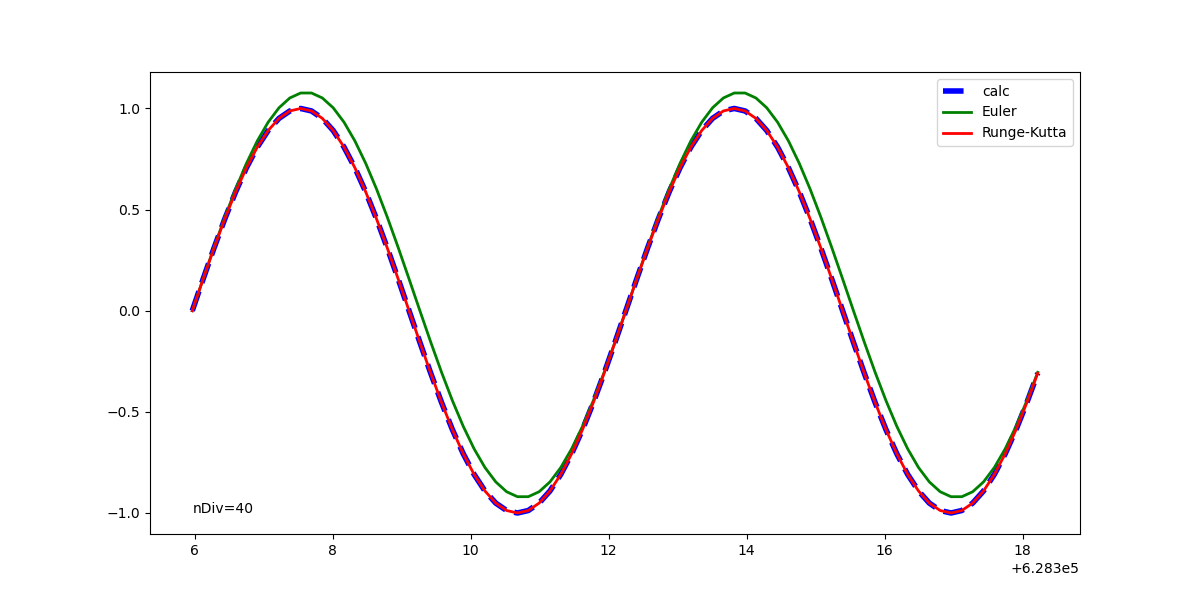
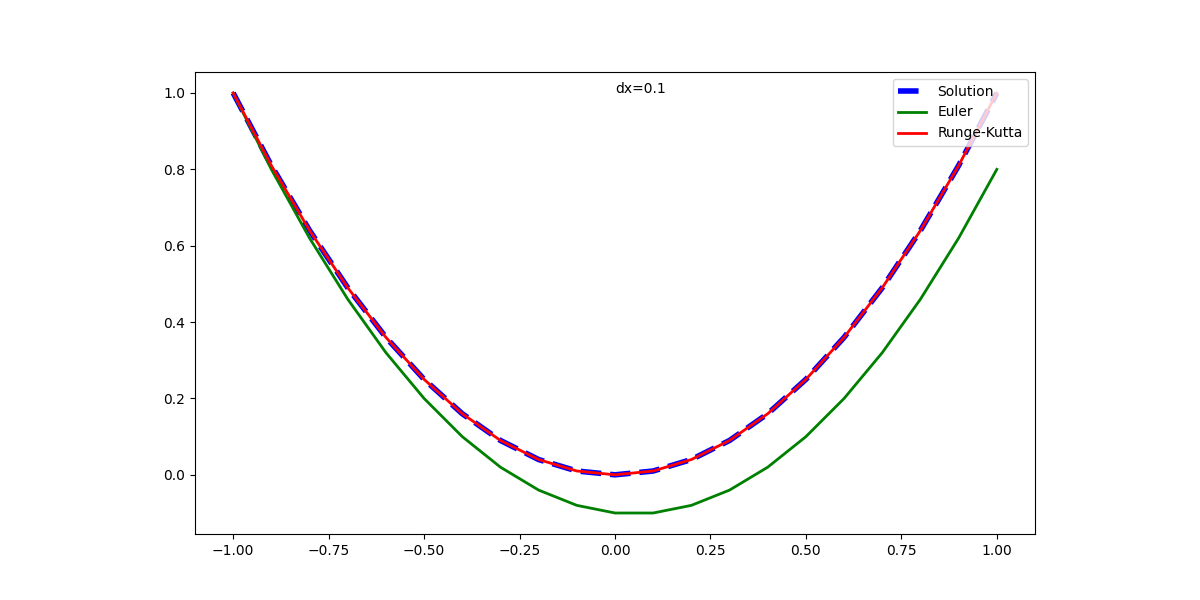
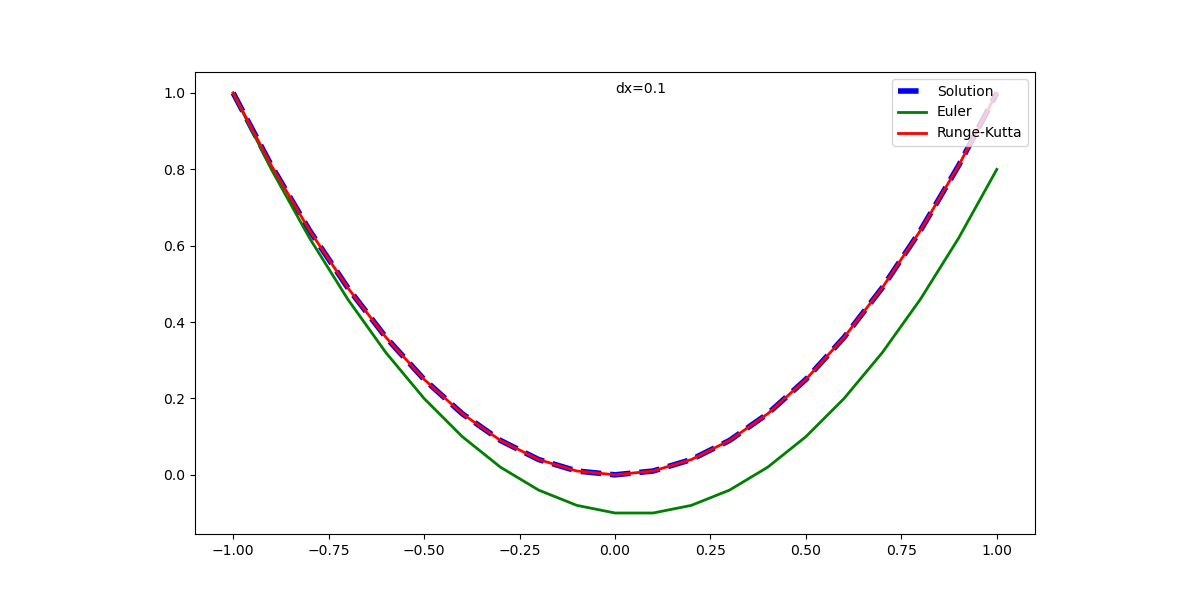
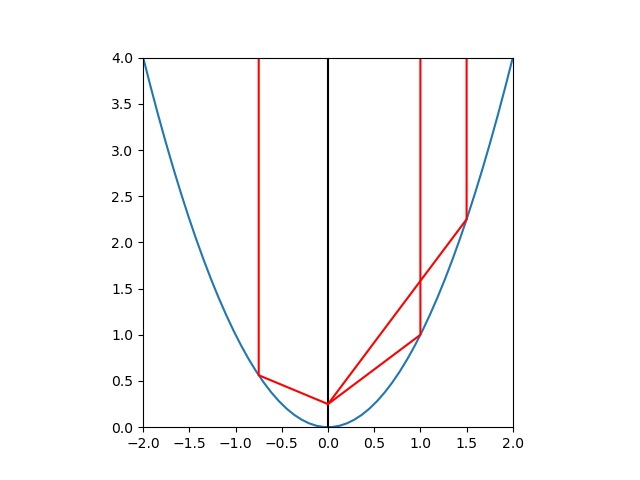
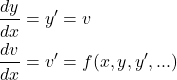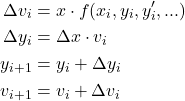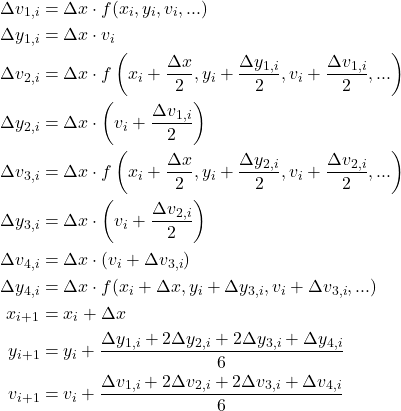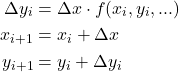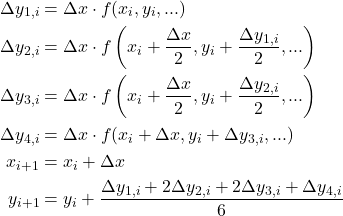Python – 図形を含むアニメーション

2023-06-30 / tau / コメントする

ArtistAnimationの場合

ArtistAnimationにグラフを追加するには、たとえばplotメソッドの戻り値をそのままリストに追加していけばよい。

artists = []
fig, ax = plt.subplots()
frame_count = 20
for i in range(frame_count):
    x = np.linspace(0, 4 * np.pi)
    y = np.sin(x - 2 * np.pi / frame_count * i)
    artist = ax.plot(x, y, color='blue')
    artists.append(artist)
anim = ArtistAnimation(fig, artists, interval=100)
plt.show()

artists = []

fig, ax = plt.subplots()

frame_count = 20

for i in range(frame_count):

x = np.linspace(0, 4 * np.pi)

y = np.sin(x - 2 * np.pi / frame_count * i)

artist = ax.plot(x, y, color='blue')

artists.append(artist)

anim = ArtistAnimation(fig, artists, interval=100)

plt.show()

ところが、matplotlib.patchesの図形の場合に同じようにすると、アニメーションにならず全フレームの図形が重ね書きされてしまう。

for i in range(frame_count):
    circle = patch.Circle(xy=(i, 0), radius=1.0)
    artist_patch = ax.add_artist(circle)
    artists.append(artist_patch)
anim = ArtistAnimation(fig, artists, interval=100)
plt.show()

for i in range(frame_count):

circle = patch.Circle(xy=(i, 0), radius=1.0)

artist_patch = ax.add_artist(circle)

artists.append(artist_patch)

anim = ArtistAnimation(fig, artists, interval=100)

plt.show()

これを解決するには、appendの際に[]で囲んでリスト化する必要がある。

for i in range(frame_count):
    circle = patch.Circle(xy=(i, 0), radius=1.0)
    artist_patch = ax.add_artist(circle)
    artists.append([artist_patch])
anim = ArtistAnimation(fig, artists, interval=100)
plt.show()

for i in range(frame_count):

circle = patch.Circle(xy=(i, 0), radius=1.0)

artist_patch = ax.add_artist(circle)

artists.append([artist_patch])

anim = ArtistAnimation(fig, artists, interval=100)

plt.show()

以下は円の図形のアニメーションのコード例。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patch
from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト
artists = []

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.set_xlim(0, 20)
ax.set_ylim(-1, 1)

# 1サイクルの動画のフレーム数
frame_count = 20
# 表示する各フレームの生成・保存
for i in range(frame_count):
    # 図形の生成
    circle = patch.Circle(xy=(i, 0), radius=1.0)
    # artist要素の取得
    artist_patch = ax.add_artist(circle)
    # フレームリストへの追加
    # 明示的にリスト化しないと要素追加となり、一括で描画されてしまう
    artists.append([artist_patch])

# フレームリストを渡してArtistAnimationインスタンスを生成
anim = ArtistAnimation(fig, artists, interval=100)

# 表示
plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as patch

from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト

artists = []

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

ax.set_aspect('equal')

ax.set_xlim(0, 20)

ax.set_ylim(-1, 1)

# 1サイクルの動画のフレーム数

frame_count = 20

# 表示する各フレームの生成・保存

for i in range(frame_count):

# 図形の生成

circle = patch.Circle(xy=(i, 0), radius=1.0)

# artist要素の取得

artist_patch = ax.add_artist(circle)

# フレームリストへの追加

# 明示的にリスト化しないと要素追加となり、一括で描画されてしまう

artists.append([artist_patch])

# フレームリストを渡してArtistAnimationインスタンスを生成

anim = ArtistAnimation(fig, artists, interval=100)

# 表示

plt.show()

実行結果は以下の通り。

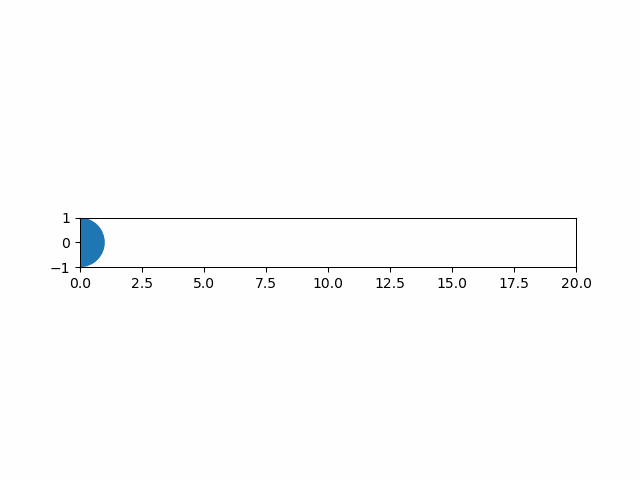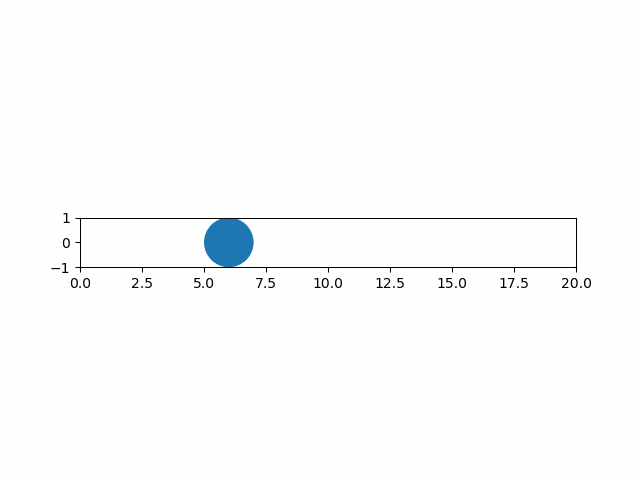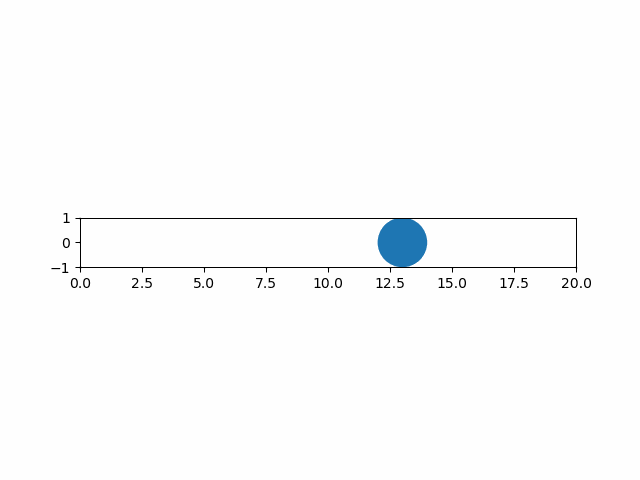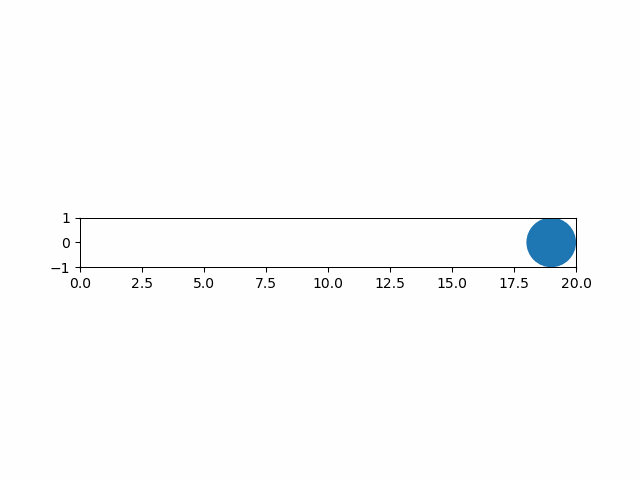
グラフと図形の重ね合わせ

グラフと図形を重ね合わせるときも、patchesの図形を明示的にリストとしてappendする必要がある。

for i in range(frame_count):
    artist_graph = ax.plot([0, i], [0, 0], color='blue')
    circle = patch.Circle(xy=(i, 0), radius=1.0)
    artist_patch = ax.add_artist(circle)
    artists.append(artist_graph + [artist_patch])

for i in range(frame_count):

artist_graph = ax.plot([0, i], [0, 0], color='blue')

circle = patch.Circle(xy=(i, 0), radius=1.0)

artist_patch = ax.add_artist(circle)

artists.append(artist_graph + [artist_patch])

以下は、plotによる線とpatches.Circleによる円を重ねて描く例。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patch
from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト
artists = []

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.set_xlim(0, 20)
ax.set_ylim(-1, 1)

# 1サイクルの動画のフレーム数
frame_count = 20
# 表示する各フレームの生成・保存
for i in range(frame_count):
    # グラフのartist取得
    artist_graph = ax.plot([0, i], [0, 0], color='blue')
    # 図形の生成
    circle = patch.Circle(xy=(i, 0), radius=1.0)
    # artist要素の取得
    artist_patch = ax.add_artist(circle)
    # フレームリストへの追加
    # 図形は明示的にリスト化しないと要素追加となり、一括で描画されてしまう
    artists.append(artist_graph + [artist_patch])

# フレームリストを渡してArtistAnimationインスタンスを生成
anim = ArtistAnimation(fig, artists, interval=100)

# 表示
plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as patch

from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト

artists = []

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

ax.set_aspect('equal')

ax.set_xlim(0, 20)

ax.set_ylim(-1, 1)

# 1サイクルの動画のフレーム数

frame_count = 20

# 表示する各フレームの生成・保存

for i in range(frame_count):

# グラフのartist取得

artist_graph = ax.plot([0, i], [0, 0], color='blue')

# 図形の生成

circle = patch.Circle(xy=(i, 0), radius=1.0)

# artist要素の取得

artist_patch = ax.add_artist(circle)

# フレームリストへの追加

# 図形は明示的にリスト化しないと要素追加となり、一括で描画されてしまう

artists.append(artist_graph + [artist_patch])

# フレームリストを渡してArtistAnimationインスタンスを生成

anim = ArtistAnimation(fig, artists, interval=100)

# 表示

plt.show()

実行結果は以下の通り。

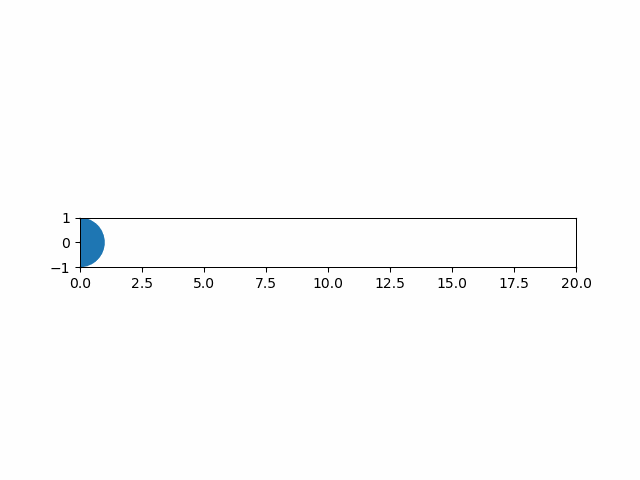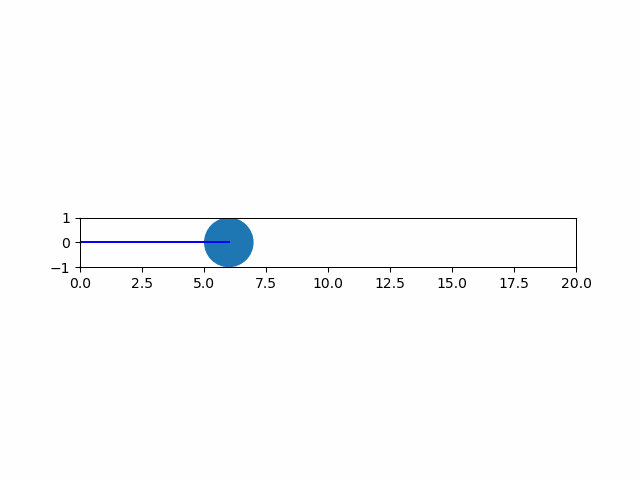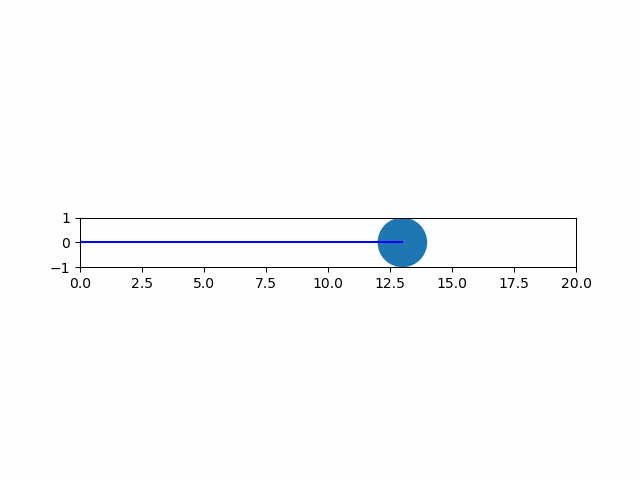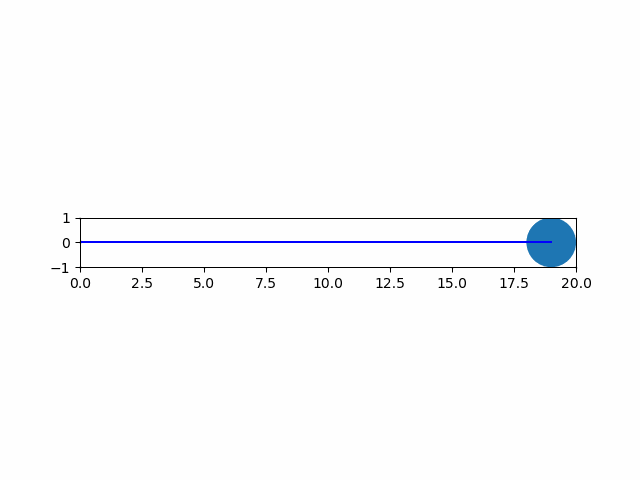
FuncAnimationの場合

FuncAnimationの場合は描画関数中でグラフを描くだけで、ArtistAnimationのようなコレクションを用いない。

この場合はArtistAnimationより簡明で、グラフはAxesオブジェクトなどに描画、図形はadd_artistメソッドで追加するだけ。

def draw_frame(frame):
    plt.cla()
    ax.set_aspect('equal')
    ax.set_xlim(0, 20)
    ax.set_ylim(-1, 1)
    ax.plot([0, frame], [0, 0], color='blue')
    circle = patch.Circle(xy=(frame, 0), radius=1.0)
    ax.add_artist(circle)
anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

def draw_frame(frame):

plt.cla()

ax.set_aspect('equal')

ax.set_xlim(0, 20)

ax.set_ylim(-1, 1)

ax.plot([0, frame], [0, 0], color='blue')

circle = patch.Circle(xy=(frame, 0), radius=1.0)

ax.add_artist(circle)

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

以下はArtistAnimationと同じく、plotによる線とpatches.Circleによる円を重ね牡蠣する例。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patch
from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト
artists = []

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()

def draw_frame(frame):
    # FuncAnimationの場合はフレームごとに内容をクリア
    plt.cla()
    # Axesに対する設定もクリアされるので、毎回設定が必要
    ax.set_aspect('equal')
    ax.set_xlim(0, 20)
    ax.set_ylim(-1, 1)
    # グラフの描画
    ax.plot([0, frame], [0, 0], color='blue')
    # 図形の生成
    circle = patch.Circle(xy=(frame, 0), radius=1.0)
    # 図形の追加
    ax.add_artist(circle)

# 描画関数を渡してFuncAnimationインスタンスを生成
anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示
plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as patch

from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト

artists = []

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

def draw_frame(frame):

# FuncAnimationの場合はフレームごとに内容をクリア

plt.cla()

# Axesに対する設定もクリアされるので、毎回設定が必要

ax.set_aspect('equal')

ax.set_xlim(0, 20)

ax.set_ylim(-1, 1)

# グラフの描画

ax.plot([0, frame], [0, 0], color='blue')

# 図形の生成

circle = patch.Circle(xy=(frame, 0), radius=1.0)

# 図形の追加

ax.add_artist(circle)

# 描画関数を渡してFuncAnimationインスタンスを生成

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示

plt.show()

Python – FuncAnimationによる動画表示

2023-06-28 / tau / コメントする

概要

Pythonのmatplotlibにはanimationパッケージがあり、ArtistAnimationとFuncAnimationの2つのクラスが準備されている。

ArtistAnimationは、予め動画に表示する各フレームを生成しておいて、これらを動画として表示する
FuncAnimationは、全結果を保存せず、フレームごとに描画を実行する関数を実行して、動画して表示する

ここでは、FuncAnimationによる動画の表示方法を整理する(ArtistAnimationについてはこちら)。

1つのグラフの表示

流れ

animationパッケージ又はArtistAnimationクラスをインポート
グラフを描画する関数を定義
FuncAnimationクラスのコンストラクターに描画関数を渡してインスタンスを生成
表示

処理ステップ

インポート

パッケージをインポートする

from matplotlib.animation import FuncAnimation
# この場合はFuncAnimation(...)と直接コンストラクターを呼ぶ

1 2	from matplotlib.animation import FuncAnimation # この場合はFuncAnimation(...)と直接コンストラクターを呼ぶ

または

import matplotlib.animation as animation
# この場合はanimation.FuncAnimation(...)のようにコンストラクターを呼ぶ

1 2	import matplotlib.animation as animation # この場合はanimation.FuncAnimation(...)のようにコンストラクターを呼ぶ

フレームリストの準備

動画の各フレームを保存するリストを準備する。animationパッケージでは、個々のグラフフレームをartistと表現している。

artists = []

1	artists = []

FigureとAxesオブジェクトを準備

フレームを描画するオブジェクトを準備しておく

fig, ax = plt.subplots()

1	fig, ax = plt.subplots()

1フレームを描画する関数を定義

4周期分の正弦関数を描画する関数を定義している。

def draw_frame(frame):
    plt.cla()
    x = np.linspace(0, 4 * np.pi)
    y = np.sin(x - frame / frame_count * 2 * np.pi)
    ax.plot(x, y, color='blue')

def draw_frame(frame):

plt.cla()

x = np.linspace(0, 4 * np.pi)

y = np.sin(x - frame / frame_count * 2 * np.pi)

ax.plot(x, y, color='blue')

ここではループごとにxを計算しているが、今回は全フレーム共通なので、ループの外で準備してもよい
plot命令のcolor指定をしないと、描画するごとに違うグラフとして色を変えて描画されてしまう

アニメーション設定して表示させる

FuncAnimationクラスのコンストラクターに必要な引数を与えてインスタンスを生成し、表示させる。intervalはフレーム間の待機時間で、ミリ秒で与える。

arim = ArtistAnimation(fig, artists, interval=100)

plt.show()

arim = ArtistAnimation(fig, artists, interval=100)

plt.show()

GIF画像として保存する

結果をGIF画像として保存するには、plt.show()を実行せず、以下のようにimagemagicでファイルとして書き出す。

frames=20でフレーム数を設定しているが、これがないとGIF保存のときにファイル容量が肥大化してしまう。それでも容量は800KB程度になり、ArtistAnimationのときの150KB程度よりも大きい。

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

plt.show()

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

plt.show()

実行結果

以下のような動画が表示される。

コード

全体の実行コードは以下のとおり。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト
frame_count = 20

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()

# 表示する各フレームを生成する関数
def draw_frame(frame):
    plt.cla()
    x = np.linspace(0, 4 * np.pi)
    y = np.sin(x - frame / frame_count * 2 * np.pi)
    ax.plot(x, y, color='blue')

# 描画関数を渡してFuncAnimationインスタンスを生成
anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示
plt.show()
#anim.save("simple.gif", writer="imagemagick")

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト

frame_count = 20

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

# 表示する各フレームを生成する関数

def draw_frame(frame):

plt.cla()

x = np.linspace(0, 4 * np.pi)

y = np.sin(x - frame / frame_count * 2 * np.pi)

ax.plot(x, y, color='blue')

# 描画関数を渡してFuncAnimationインスタンスを生成

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示

plt.show()

#anim.save("simple.gif", writer="imagemagick")

複数のグラフの表示

流れ

全体の流れは単一のグラフの場合と同じ。リスト保存時に複数グラフを加算して重ね合わせるところだけが異なる。

animationパッケージ又はArtistAnimationクラスをインポート
グラフを描画する関数を定義し、複数のグラフをプロット
FuncAnimationクラスのコンストラクターに描画関数を渡してインスタンスを生成
表示

処理ステップ

以下の描画関数が単一グラフの場合と異なる。関数の中で、異なる2つのグラフを描画している

def draw_frame(frame):
    x = np.linspace(0, 4 * np.pi)
    plt.cla()
    y1 = np.sin(x - frame / frame_count * 2 * np.pi)
    y2 = np.sin(x - frame / frame_count * 2 * np.pi + np.pi / 2)
    ax.plot(x, y1, color='blue')
    ax.plot(x, y2, color='green')

def draw_frame(frame):

x = np.linspace(0, 4 * np.pi)

plt.cla()

y1 = np.sin(x - frame / frame_count * 2 * np.pi)

y2 = np.sin(x - frame / frame_count * 2 * np.pi + np.pi / 2)

ax.plot(x, y1, color='blue')

ax.plot(x, y2, color='green')

実行結果

以下のように、2つのグラフが同時に表示される。

コード

全体の実行コードは以下のとおり。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト
frame_count = 20

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()

# 表示する各フレームを生成する関数
def draw_frame(frame):
    x = np.linspace(0, 4 * np.pi)
    plt.cla()
    y1 = np.sin(x - frame / frame_count * 2 * np.pi)
    y2 = np.sin(x - frame / frame_count * 2 * np.pi + np.pi / 2)
    ax.plot(x, y1, color='blue')
    ax.plot(x, y2, color='green')

# 描画関数を渡してFuncAnimationインスタンスを生成
anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示
plt.show()
#anim.save("multi.gif", writer="imagemagick")

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.animation import FuncAnimation

# 各フレームを保存するフレームリスト

frame_count = 20

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

# 表示する各フレームを生成する関数

def draw_frame(frame):

x = np.linspace(0, 4 * np.pi)

plt.cla()

y1 = np.sin(x - frame / frame_count * 2 * np.pi)

y2 = np.sin(x - frame / frame_count * 2 * np.pi + np.pi / 2)

ax.plot(x, y1, color='blue')

ax.plot(x, y2, color='green')

# 描画関数を渡してFuncAnimationインスタンスを生成

anim = FuncAnimation(fig, draw_frame, interval=100, frames=20)

# 表示

plt.show()

#anim.save("multi.gif", writer="imagemagick")

描画関数に引数を渡す

描画関数に独自の引数を渡すことができる。

たとえば最初の「1つのグラフの表示」で、frame_countと表示する最大時刻max_xを引数とする場合、まず描画関数でこれらを引数として宣言し、関数内でこれを使った処理を書く。

def draw_frame(frame, max_x, frame_count):
    plt.cla()
    x = np.linspace(0, max_x)
    y = np.sin(x - frame / frame_count * 2 * np.pi)
    ax.plot(x, y, color='blue')

def draw_frame(frame, max_x, frame_count):

plt.cla()

x = np.linspace(0, max_x)

y = np.sin(x - frame / frame_count * 2 * np.pi)

ax.plot(x, y, color='blue')

FuncAnimationインスタンス生成時に、fargsで独自宣言した引数の値をタプルで与える。

anim = FuncAnimation(fig, draw_frame, fargs=(4 * np.pi, 20), interval=100, frames=20)

1	anim = FuncAnimation(fig, draw_frame, fargs=(4 * np.pi, 20), interval=100, frames=20)

Python – ArtistAnimationによる動画表示

2023-06-28 / tau / コメントする

概要

Pythonのmatplotlibにはanimationパッケージがあり、ArtistAnimationとFuncAnimationの2つのクラスが準備されている。

ArtistAnimationは、予め動画に表示する各フレームを生成しておいて、これらを動画として表示する
FuncAnimationは、全結果を保存せず、フレームごとに描画を実行する関数を実行して、動画して表示する

ここでは、ArtistAnimationによる動画の表示方法を整理する(FuncAnimationについてはこちら)。

1つのグラフの表示

流れ

animationパッケージ又はArtistAnimationクラスをインポート
フレームの数だけグラフを描画してリストに保存
フレームリストを渡してArtistAnimationインスタンスを生成
表示

処理ステップ

インポート

パッケージをインポートする

from matplotlib.animation import ArtistAnimation
# この場合はArtistAnimation(...)と直接コンストラクターを呼ぶ

1 2	from matplotlib.animation import ArtistAnimation # この場合はArtistAnimation(...)と直接コンストラクターを呼ぶ

または

import matplotlib.animation as animation
# この場合はanimation.ArtistAnimation(...)のようにコンストラクターを呼ぶ

1 2	import matplotlib.animation as animation # この場合はanimation.ArtistAnimation(...)のようにコンストラクターを呼ぶ

フレームリストの準備

動画の各フレームを保存するリストを準備する。animationパッケージでは、個々のグラフフレームをartistと表現している。

artists = []

1	artists = []

FigureとAxesオブジェクトを準備

フレームを描画するオブジェクトを準備しておく

fig, ax = plt.subplots()

1	fig, ax = plt.subplots()

フレーム数を指定して各フレームを保存する

以下ではフレーム数を20として、20回分のグラフを少しずつずらして描画して保存している。

frame_count = 20
for i in range(frame_count):
    x = np.linspace(0, 4 * np.pi)
    y = np.sin(x - 2 * np.pi / frame_count * i)
    artist = ax.plot(x, y, color='blue')
    artists.append(artist)

frame_count = 20

for i in range(frame_count):

x = np.linspace(0, 4 * np.pi)

y = np.sin(x - 2 * np.pi / frame_count * i)

artist = ax.plot(x, y, color='blue')

artists.append(artist)

ここではグラフを正弦波として、1周期分を20分割して表示させている。

ここではループごとにxを計算しているが、今回は全フレーム共通なので、ループの外で準備してもよい
plot命令のcolor指定をしないと、描画するごとに違うグラフとして色を変えて描画されてしまう
描画結果はオブジェクトとして、先に準備したartistコレクションに追加している

アニメーション設定して表示させる

ArtistAnimationクラスのコンストラクターに必要な引数を与えてインスタンスを生成し、表示させる。intervalはフレーム間の待機時間で、ミリ秒で与える。

arim = ArtistAnimation(fig, artists, interval=100)

plt.show()

arim = ArtistAnimation(fig, artists, interval=100)

plt.show()

GIF画像として保存する

結果をGIF画像として保存するには、plt.show()を実行せず、以下のようにimagemagicでファイルとして書き出す。

anim = ArtistAnimation(fig, artists, interval=100)

anim.save("test.gif", writer="imagemagick")

anim = ArtistAnimation(fig, artists, interval=100)

anim.save("test.gif", writer="imagemagick")

実行結果

以下のような動画が表示される。

コード

全体の実行コードは以下のとおり。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト
artists = []

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()

# 1サイクルの動画のフレーム数
frame_count = 20
# 表示する各フレームの生成・保存
for i in range(frame_count):
    # グラフの描画
    x = np.linspace(0, 4 * np.pi)
    y = np.sin(x - 2 * np.pi / frame_count * i)
    # グラフの保存
    artist = ax.plot(x, y, color='blue')
    # フレームリストへの追加
    artists.append(artist)

# フレームリストを渡してArtistAnimationインスタンスを生成
anim = ArtistAnimation(fig, artists, interval=100)

# 表示
plt.show()
#anim.save("simple.gif", writer="imagemagick")

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト

artists = []

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

# 1サイクルの動画のフレーム数

frame_count = 20

# 表示する各フレームの生成・保存

for i in range(frame_count):

# グラフの描画

x = np.linspace(0, 4 * np.pi)

y = np.sin(x - 2 * np.pi / frame_count * i)

# グラフの保存

artist = ax.plot(x, y, color='blue')

# フレームリストへの追加

artists.append(artist)

# フレームリストを渡してArtistAnimationインスタンスを生成

anim = ArtistAnimation(fig, artists, interval=100)

# 表示

plt.show()

#anim.save("simple.gif", writer="imagemagick")

複数のグラフの表示

流れ

全体の流れは単一のグラフの場合と同じ。リスト保存時に複数グラフを加算して重ね合わせるところだけが異なる。

animationパッケージ又はArtistAnimationクラスをインポート
フレームの数だけグラフを描画して、重ね合わせてリストに保存
フレームリストを渡してArtistAnimationインスタンスを生成
表示

処理ステップ

以下の部分だけが単一グラフの場合と異なる。2つのグラフを描画し、そのオブジェクトを加算して1フレームとした上でartistsに追加している

for i in range(frame_count):
    x = np.linspace(0, 4 * np.pi)
    y1 = np.sin(x - 2 * np.pi / frame_count * i)
    y2 = np.sin(x - 2 * np.pi / frame_count * i + np.pi / 2)
    artist1 = ax.plot(x, y1, color='blue')
    artist2 = ax.plot(x, y2, color='green')
    artists.append(artist1 + artist2)

for i in range(frame_count):

x = np.linspace(0, 4 * np.pi)

y1 = np.sin(x - 2 * np.pi / frame_count * i)

y2 = np.sin(x - 2 * np.pi / frame_count * i + np.pi / 2)

artist1 = ax.plot(x, y1, color='blue')

artist2 = ax.plot(x, y2, color='green')

artists.append(artist1 + artist2)

実行結果

以下のように、2つのグラフが同時に表示される。

コード

全体の実行コードは以下のとおり。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト
artists = []

# FigureとAxesインスタンスを取得
fig, ax = plt.subplots()

# 1サイクルの動画のフレーム数
frame_count = 20
# 表示する各フレームの生成・保存
for i in range(frame_count):
    # グラフの描画
    x = np.linspace(0, 4 * np.pi)
    y1 = np.sin(x - 2 * np.pi / frame_count * i)
    y2 = np.sin(x - 2 * np.pi / frame_count * i + np.pi / 2)
    # グラフの保存
    artist1 = ax.plot(x, y1, color='blue')
    artist2 = ax.plot(x, y2, color='green')
    # フレームリストへの追加
    artists.append(artist1 + artist2)

# フレームリストを渡してArtistAnimationインスタンスを生成
anim = ArtistAnimation(fig, artists, interval=100)

# 表示
plt.show()
#anim.save("multi.gif", writer="imagemagick")

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.animation import ArtistAnimation

# 各フレームを保存するフレームリスト

artists = []

# FigureとAxesインスタンスを取得

fig, ax = plt.subplots()

# 1サイクルの動画のフレーム数

frame_count = 20

# 表示する各フレームの生成・保存

for i in range(frame_count):

# グラフの描画

x = np.linspace(0, 4 * np.pi)

y1 = np.sin(x - 2 * np.pi / frame_count * i)

y2 = np.sin(x - 2 * np.pi / frame_count * i + np.pi / 2)

# グラフの保存

artist1 = ax.plot(x, y1, color='blue')

artist2 = ax.plot(x, y2, color='green')

# フレームリストへの追加

artists.append(artist1 + artist2)

# フレームリストを渡してArtistAnimationインスタンスを生成

anim = ArtistAnimation(fig, artists, interval=100)

# 表示

plt.show()

#anim.save("multi.gif", writer="imagemagick")

図形を含むアニメーション

matplotlib.patchesによる図形を含んでアニメーション表示するには、少し工夫がいる。その方法はこちら。

Runge-Kutta法による1階常微分方程式の解

2023-06-25 / tau / コメントする

概要

1階常微分方程式について、4次のRunge-Kutta法(RK4)による数値解と解析解を比較する。Euler法による解についても重ねてみた。

RK4は、かなり粗い分割間隔でもよい結果になる
Euler法は、分割間隔を小さくとらないと精度が上がらない

Logistic関数

方程式と解析解

Logistic関数に関する微分方程式は以下で表される。

(1) $\begin{equation*} \frac{N(t)}{dt} = r \left( 1 - \dfrac{N(t)}{K} \right) N(t) \end{equation*}$

この方程式は解析的に解けて、以下の解を得る。

(2) $\begin{equation*} N(t) = \dfrac{K}{1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt}} \end{equation*}$

数値解

式(1)をRK4、Euler法によって解き、解析解と重ねる（解き方は1階常微分方程式の数値解法を参照）。

r=10, K=1000として計算した結果は以下の通り。

RK4は上限に収束するまでの時間(t=1.0)の20等分くらい(dt=0.05)でもよく合っている
Euler法では凹な部分で計算値が過少となり、凸の部分で解析解に追いついているが、適合度はよろしくない。

dtを上記の10分の1(dt=0.05)として計算した結果が以下の通り。Euler法もかなり適合度合いがよくなったが、それでもまだ少し右方にずれている。

逆にdt=0.1と大きくしてみた。折れ線がはっきりわかるくらいの粗さだが、RK4はよくフィットしている。Euler法のずれは大きくなっている。

コード

上記の結果は、以下のコードを実行して得ている。

# ロジスティック関数の1階常微分方程式

import numpy as np
import matplotlib.pyplot as plt
import diffeq

# 解析解を計算する関数
def logistic(t, r, K, N_initial):
    return K / (1 + (K / N_initial - 1) * np.exp(-r * t))

# 微分方程式の右辺の関数
def derivative(x, y, r, K):
    return r * (1 - y / K) * y

# 関数に渡すパラメーター
params = {'r': 10, 'K': 1000}

# 計算に必要な値の設定
t_start = 0     # 計算開始点のtの値
t_end = 1.5     # 計算終了点のtの値
dt = 0.05       # 分割幅

# 計算開始点におけるNの初期値をセット
N_initial = 2

# 以下、計算用リストの確保
num_points = int((t_end - t_start) / dt) + 1
t_calc = np.linspace(t_start, t_end, num=num_points-1, endpoint=False)
N_euler = np.linspace(t_start, t_end, num=num_points)
N_rk = [0.0] * N_euler.size

# 計算開始点に初期値をセット
N_euler[0] = N_initial
N_rk[0] = N_initial

# 比較用の解析解表示のための定義域と計算値
t_domain = np.linspace(t_start, t_end, num=num_points)
N_logistic = logistic(t=t_domain, N_initial=N_initial, **params)

# 計算開始
for i, t in enumerate(t_calc):
    # Euler法
    N_euler[i + 1] = diffeq.euler1(
        x=t, y=N_euler[i], dx=dt,  func=derivative, params=params)
    # Runge-Kutta法
    N_rk[i + 1] = diffeq.rk4_1(
        x=t, y=N_rk[i], dx=dt, func=derivative, params=params)

# グラフ描画
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(t_domain, N_logistic, label="Solution", color="blue", linestyle="dashed", linewidth=4)
ax.plot(t_domain, N_euler, label="Euler", color="green", linestyle="solid", linewidth=2)
ax.plot(t_domain, N_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)
ax.text(0, params['K'], 'dt=' + str(dt))
ax.legend(loc="lower right")
plt.show()

# ロジスティック関数の1階常微分方程式

import numpy as np

import matplotlib.pyplot as plt

import diffeq

# 解析解を計算する関数

def logistic(t, r, K, N_initial):

return K / (1 + (K / N_initial - 1) * np.exp(-r * t))

# 微分方程式の右辺の関数

def derivative(x, y, r, K):

return r * (1 - y / K) * y

# 関数に渡すパラメーター

params = {'r': 10, 'K': 1000}

# 計算に必要な値の設定

t_start = 0 # 計算開始点のtの値

t_end = 1.5 # 計算終了点のtの値

dt = 0.05 # 分割幅

# 計算開始点におけるNの初期値をセット

N_initial = 2

# 以下、計算用リストの確保

num_points = int((t_end - t_start) / dt) + 1

t_calc = np.linspace(t_start, t_end, num=num_points-1, endpoint=False)

N_euler = np.linspace(t_start, t_end, num=num_points)

N_rk = [0.0] * N_euler.size

# 計算開始点に初期値をセット

N_euler[0] = N_initial

N_rk[0] = N_initial

# 比較用の解析解表示のための定義域と計算値

t_domain = np.linspace(t_start, t_end, num=num_points)

N_logistic = logistic(t=t_domain, N_initial=N_initial, **params)

# 計算開始

for i, t in enumerate(t_calc):

# Euler法

N_euler[i + 1] = diffeq.euler1(

x=t, y=N_euler[i], dx=dt, func=derivative, params=params)

# Runge-Kutta法

N_rk[i + 1] = diffeq.rk4_1(

x=t, y=N_rk[i], dx=dt, func=derivative, params=params)

# グラフ描画

fig, ax = plt.subplots(figsize=(8, 6))

ax.plot(t_domain, N_logistic, label="Solution", color="blue", linestyle="dashed", linewidth=4)

ax.plot(t_domain, N_euler, label="Euler", color="green", linestyle="solid", linewidth=2)

ax.plot(t_domain, N_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)

ax.text(0, params['K'], 'dt=' + str(dt))

ax.legend(loc="lower right")

plt.show()

三角関数

方程式と解析解

簡単な正弦関数を考える。

(3) $\begin{equation*} y = \sin t \end{equation*}$

この関数は、以下の微分方程式の解である。

(4) $\begin{equation*} y' = \cos t \quad ( t=0 \Rightarrow y=0 ) \end{equation*}$

数値解

式(4)をEuler法、Runge-Kutta法によって解き、式(3)のグラフと重ねる。

以下は分割間隔を1/40周期で計算した結果。RK4の精度はいいが、Euler法では上に凸のときに過大となり、下に凸のときに過少となって初期値に戻っている。

分割幅を1/200周期にするとEuler法でも精度は上がってくるが、まだ少し誤差が残っている。

分割数を10とかなり粗くとっても、RK4の適合度合いはよい。

繰り返し数が増えた時に誤差が累積するかどうか確認してみた。

以下は10万周期分計算した最後の2周忌を取り出した結果で、RK4、Euler法とも傾向は変わらない。規則正しい周期関数の場合は、繰り返し数を増やしても誤差は拡散しないと思われる。

コード

以下はこれまでの計算をしたPythonのコード。

計算区間を長くとって一部だけ表示させるため、Logistic関数のときとは異なる処理をしている。

ループの各段階で計算結果をリストに保存せず、各ステップで計算された次のステップの結果を元の変数に入れ替える
予め指定した計算区間の間の結果だけ、表示用のリストに保存する

# Runge-Kutta法で多数回計算を繰り返した際の精度を確認
# 全ての結果はリストに保存せず、必要な区間だけを保存

import numpy as np
import matplotlib.pyplot as plt
import diffeq

# 解析解を計算する関数
def sine(x):
    return np.sin(t)

# 微分方程式の右辺の関数
def derivative(x, y):
    return np.cos(x)

# 計算区間と計算間隔
t_start = 0
t_end = 2 * np.pi * 100000
dt = 2 * np.pi / 40
# 表示させる区間
t_view_start = 2 * np.pi * 99998
t_view_end = 2 * np.pi * 100000

# t=0におけるyの初期値
y_initial = 0.0

# 計算点数は準備するが、繰り返し計算の答えを全部は保存しない
num_points = int((t_end - t_start) / dt) + 1

# 計算開始点に初期値をセット
y_now_euler = y_initial
y_now_rk = y_initial

# 表示する区間だけ計算結果を保存するリスト
t_view = []
y_view_calc = []
y_view_euler = []
y_view_rk = []

# 計算開始
for i in range(0, num_points - 1):
    # iステップ目の時刻を計算
    t = t_start + dt * i
    # 時刻が指定した区間内のときだけ配列に結果を追加
    if t >= t_view_start and t <= t_view_end:
        t_view.append(t)
        y_view_calc.append(sine(t))
        y_view_euler.append(y_now_euler)
        y_view_rk.append(y_now_rk)

    # i+1ステップ目の計算値
    y_euler = diffeq.euler1(
        x=t, y=y_now_euler, dx=dt, func=derivative, params=None)
    y_rk = diffeq.rk4_1(
        x=t, y=y_now_rk, dx=dt, func=derivative, params=None)

    # 次のステップのため、計算結果を入れ替え
    y_now_euler = y_euler
    y_now_rk = y_rk

# グラフ描画
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(t_view, y_view_calc, label="calc", color="blue", linestyle="dashed", linewidth=4)
ax.plot(t_view, y_view_euler, label="Euler", color="green", linestyle="solid", linewidth=2)
ax.plot(t_view, y_view_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)
ax.text(t_view_start, -1, 'nDiv=' + str(round(2 * np.pi / dt)))
ax.legend(loc="upper right")
plt.show()

# Runge-Kutta法で多数回計算を繰り返した際の精度を確認

# 全ての結果はリストに保存せず、必要な区間だけを保存

import numpy as np

import matplotlib.pyplot as plt

import diffeq

# 解析解を計算する関数

def sine(x):

return np.sin(t)

# 微分方程式の右辺の関数

def derivative(x, y):

return np.cos(x)

# 計算区間と計算間隔

t_start = 0

t_end = 2 * np.pi * 100000

dt = 2 * np.pi / 40

# 表示させる区間

t_view_start = 2 * np.pi * 99998

t_view_end = 2 * np.pi * 100000

# t=0におけるyの初期値

y_initial = 0.0

# 計算点数は準備するが、繰り返し計算の答えを全部は保存しない

num_points = int((t_end - t_start) / dt) + 1

# 計算開始点に初期値をセット

y_now_euler = y_initial

y_now_rk = y_initial

# 表示する区間だけ計算結果を保存するリスト

t_view = []

y_view_calc = []

y_view_euler = []

y_view_rk = []

# 計算開始

for i in range(0, num_points - 1):

# iステップ目の時刻を計算

t = t_start + dt * i

# 時刻が指定した区間内のときだけ配列に結果を追加

if t >= t_view_start and t <= t_view_end:

t_view.append(t)

y_view_calc.append(sine(t))

y_view_euler.append(y_now_euler)

y_view_rk.append(y_now_rk)

# i+1ステップ目の計算値

y_euler = diffeq.euler1(

x=t, y=y_now_euler, dx=dt, func=derivative, params=None)

y_rk = diffeq.rk4_1(

x=t, y=y_now_rk, dx=dt, func=derivative, params=None)

# 次のステップのため、計算結果を入れ替え

y_now_euler = y_euler

y_now_rk = y_rk

# グラフ描画

fig, ax = plt.subplots(figsize=(12, 6))

ax.plot(t_view, y_view_calc, label="calc", color="blue", linestyle="dashed", linewidth=4)

ax.plot(t_view, y_view_euler, label="Euler", color="green", linestyle="solid", linewidth=2)

ax.plot(t_view, y_view_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)

ax.text(t_view_start, -1, 'nDiv=' + str(round(2 * np.pi / dt)))

ax.legend(loc="upper right")

plt.show()

2階常微分方程式の数値解法

2023-06-24 / tau / コメントする

概要

2階常微分方程式の数値解法、Euler法とRunge-Kutta法をPythonのモジュールとしてまとめた。

1階常微分方程式の解法についてはこちら。

基本形

以下のような方程式を考える。

(1) $\begin{equation*} \dfrac{d^2 y}{dx^2} = f\left ( x, y, \dfrac{dy}{dx}, ... \right ) \end{equation*}$

(2) $\begin{equation*} y'' = f(x, y, y', ... ) \end{equation*}$

y‘(x)をv(x)と置いて以下のように変形する。

(3) $\begin{align*} \frac{dy}{dx} &=y' = v \\ \frac{dv}{dx} &= v' = f(x, y, y', ...) \end{align*}$

Euler法

Euler法では、iステップ目のΔv→Δyと計算し、それらを使ってi+1ステップ目のyとvを計算する。

(4) $\begin{align*} \Delta v_i &= \Delata x \cdot f(x_i, y_i, y'_i, ...) \\ \Delta y_i &= \Delta x \cdot v_i \\ y_{i+1} &= y_i + \Delta y_i \\ v_{i+1} &= v_i + \Delta v_i \end{align*}$

Runge-Kutta法

Runge-Kutta法も同様に、iステップ目のΔv₁→Δy₁を計算し、それらを使ってΔv_i、Δy_i (i = 1, 2, 3, 4)を計算していく。

(5) $\begin{align*} \Delta v_{1, i} &= \Delta x \cdot f(x_i, y_i, v_i, ...) \\ \Delta y_{1, i} &= \Delta x \cdot v_i \\ \Delta v_{2, i} &= \Delta x \cdot f \left ( x_i + \dfrac{\Delta x}{2}, y_i + \dfrac{\Delta y_{1, i}}{2}, v_i + \dfrac{\Delta v_{1, i}}{2}, ... \right ) \\ \Delta y_{2, i} &= \Delta x \cdot \left (v_i + \dfrac{\Delta v_{1, i}}{2} \right ) \\ \Delta v_{3, i} &= \Delta x \cdot f \left ( x_i + \dfrac{\Delta x}{2}, y_i + \dfrac{\Delta y_{2, i}}{2}, v_i + \dfrac{\Delta v_{2, i}}{2}, ... \right ) \\ \Delta y_{3, i} &= \Delta x \cdot \left (v_i + \dfrac{\Delta v_{2, i}}{2} \right ) \\ \Delta v_{4, i} &= \Delta x \cdot (v_i + \Delta v_{3, i}) \\ \Delta y_{4, i} &= \Delta x \cdot f(x_i + \Delta x, y_i + \Delta y_{3, i}, v_i + \Delta v_{3, i}, ...) \\ x_{i+1} &= x_i + \Delta x \\ y_{i+1} &= y_i + \frac{\Delta y_{1, i} + 2 \Delta y_{2, i} + 2 \Delta y_{3, i} + \Delta y_{4, i}}{6} \\ v_{i+1} &= v_i + \frac{\Delta v_{1, i} + 2 \Delta v_{2, i} + 2 \Delta v_{3, i} + \Delta v_{4, i}}{6} \end{align*}$

数値解法モジュール

コード

Euler法とRunge-Kutta法で2階常微分方程式を解くモジュールを、Pythonで以下の様に書いた。

# 2階常微分方程式
# - y'' = f(x, y, ...)の形の方程式が対象
# - ある計算ステップのx(i), y(i), y'(i)を与え、次のステップのy(i+1), y'(i+1)の値を返す
# - 呼び出し側で、右辺f=func(x, y, v, param1, param2, ...)のように定義されている必要がある
#   ただしv=y'
# 使用例
# - y'' = derivative(x, y, param1, param2)の場合
# - params = {'param1': 2.0, 'param2': 3.14}のようにパラメーターを定義
# - 以下のように呼び出して、ステップ計算を進める
# - (y_next, v_next) = euler2(x=x_now, y=y_now, v=v_now, derivative, params)あるいは
# - (y_next, v_next) = rk4_2(x=x_now, y=y_now, v=v_now, derivative, params)
# funcに与える関数がパラメータを持たない場合、上の引数でparams=Noneを指定

# Euler法により2階常微分微分方程式を解く
def euler2(x, y, v, dx, func, params):
    if params is None:
        dv = dx * func(x=x, y=y, v=v)
        dy = dx * v
    else:
        dv = dx * func(x=x, y=y, v=v, **params)
        dy = dx * v
    return (y + dy, v + dv)

# 4次のRunge-Kutta法により2階常微分方程式を解く
def rk4_2(x, y, v, dx, func, params):
    if params is None:
        dv1 = dx * func(x=x, y=y, v=v)
        dy1 = dx * v
        dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2)
        dy2 = dx * (v + dv1 / 2)
        dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2)
        dy3 = dx * (v + dv2 / 2)
        dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3)
        dy4 = dx * (v + dv3)
    else:
        dv1 = dx * func(x=x, y=y, v=v, **params)
        dy1 = dx * v
        dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2, **params)
        dy2 = dx * (v + dv1 / 2)
        dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2, **params)
        dy3 = dx * (v + dv2 / 2)
        dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3, **params)
        dy4 = dx * (v + dv3)
    return (
        y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6,
        v + (dv1 + 2 * dv2 + 2 * dv3 + dv4) / 6
    )

# 2階常微分方程式

# - y'' = f(x, y, ...)の形の方程式が対象

# - ある計算ステップのx(i), y(i), y'(i)を与え、次のステップのy(i+1), y'(i+1)の値を返す

# - 呼び出し側で、右辺f=func(x, y, v, param1, param2, ...)のように定義されている必要がある

# ただしv=y'

# 使用例

# - y'' = derivative(x, y, param1, param2)の場合

# - params = {'param1': 2.0, 'param2': 3.14}のようにパラメーターを定義

# - 以下のように呼び出して、ステップ計算を進める

# - (y_next, v_next) = euler2(x=x_now, y=y_now, v=v_now, derivative, params)あるいは

# - (y_next, v_next) = rk4_2(x=x_now, y=y_now, v=v_now, derivative, params)

# funcに与える関数がパラメータを持たない場合、上の引数でparams=Noneを指定

# Euler法により2階常微分微分方程式を解く

def euler2(x, y, v, dx, func, params):

if params is None:

dv = dx * func(x=x, y=y, v=v)

dy = dx * v

else:

dv = dx * func(x=x, y=y, v=v, **params)

dy = dx * v

return (y + dy, v + dv)

# 4次のRunge-Kutta法により2階常微分方程式を解く

def rk4_2(x, y, v, dx, func, params):

if params is None:

dv1 = dx * func(x=x, y=y, v=v)

dy1 = dx * v

dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2)

dy2 = dx * (v + dv1 / 2)

dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2)

dy3 = dx * (v + dv2 / 2)

dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3)

dy4 = dx * (v + dv3)

else:

dv1 = dx * func(x=x, y=y, v=v, **params)

dy1 = dx * v

dv2 = dx * func(x=x+dx/2, y=y+dy1/2, v=v+dv1/2, **params)

dy2 = dx * (v + dv1 / 2)

dv3 = dx * func(x=x+dx/2, y=y+dy2/2, v=v+dv2/2, **params)

dy3 = dx * (v + dv2 / 2)

dv4 = dx * func(x=x+dx, y=y+dy3, v=v+dv3, **params)

dy4 = dx * (v + dv3)

return (

y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6,

v + (dv1 + 2 * dv2 + 2 * dv3 + dv4) / 6

)

関数euler2、rk4_2の使い方はいずれも同じで、以下の通り。

x, y, v：現在の計算ステップでの独立変数x、xにおけるyの値、xにおけるyの1次微分値
dx：計算の分割幅
func：微分方程式の右辺の関数
params：関数funcに与えるパラメーター

パラメーターは、呼び出し側の関数定義で設定したパラメーター名をキーとした辞書で与える。その前提で、モジュール内で**paramsとしてアンパックしている。

戻り値は実数型の数値。

使い方

モジュールの使い方の概要は以下のとおり。

右辺の関数を定義する
関数に渡すパラメーターを設定する
計算開始点と終了点のxの値、分割幅dx, yとvの初期値を設定する
x, y, vの計算用リストを確保する
計算開始点のyとvのリストに初期値をセットする
計算実行

単純な放物線の微分方程式を例にしてモジュールの使い方を示す。まず、解の方程式として以下を考える。

(6) $\begin{equation*} y = a x^2 \quad (-1 \le x \le 1) \end{equation*}$

この式を2階微分した、以下の常微分方程式を解いていく。

(7) $\begin{equation*} y'' = 2a \quad \left( x = -1 \Rightarrow \left\{ \begin{array}{l} y = a\\ y' =-2a \end{array} \right) \end{equation*}$

まず、必要なパッケージをインポート。diffeqは上で示したモジュールを収めている。

import numpy as np
import matplotlib.pyplot as plt
import diffeq

import numpy as np

import matplotlib.pyplot as plt

import diffeq

次に、微分方程式右辺の関数を定義する(以下のderivative)。この関数はパラメーターとして係数aを1つ持っている。また、パラメーターの値を辞書で定義する。

# 微分方程式の右辺の関数
def derivative(x, y, v, a):
    return 2 * a

# 関数に渡すパラメーター
params = {'a': 1.0}

# 微分方程式の右辺の関数

def derivative(x, y, v, a):

return 2 * a

# 関数に渡すパラメーター

params = {'a': 1.0}

数値計算に計算開始点x_startと終了点x_end、分割幅dx、yとvの計算初期値を設定。

# 計算に必要な値の設定
x_start = -1.0  # 計算開始点のxの値
x_end = 1.0     # 計算終了点のxの値
dx = 0.2        # 分割幅
y_initial = 1.0 # 計算開始点におけるyの初期値
v_initial = -2.0# 計算開始点におけるvの値

# 計算に必要な値の設定

x_start = -1.0 # 計算開始点のxの値

x_end = 1.0 # 計算終了点のxの値

dx = 0.2 # 分割幅

y_initial = 1.0 # 計算開始点におけるyの初期値

v_initial = -2.0# 計算開始点におけるvの値

次に、予めxの計算点のリストを用意して、これに対応するy, vの値を計算・保存していく。計算点数は植木算で分割数＋1とし、ループ計算に用いるリストは計算終了点を除いている。結果を保存しないなら、リストではなく逐次各ステップの計算値を次のステップの入力値にする。

また、計算開始点におけるy, vの初期値をセットしている。

# 以下、計算用リストの確保
# 計算点数
num_points = int((x_end - x_start) / dx) + 1
# for分で回すためのxのリスト
# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない
x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)
# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)
y_euler = np.linspace(x_start, x_end, num=num_points)
v_euler = [0.0] * y_euler.size
y_rk = [0.0] * y_euler.size
v_runge_kutta = [0.0] * y_euler.size

# 計算開始点に初期値をセット
y_euler[0] = y_initial
v_euler[0] = v_initial
y_rk[0] = y_initial
v_runge_kutta[0] = v_initial

# 以下、計算用リストの確保

# 計算点数

num_points = int((x_end - x_start) / dx) + 1

# for分で回すためのxのリスト

# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない

x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)

# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)

y_euler = np.linspace(x_start, x_end, num=num_points)

v_euler = [0.0] * y_euler.size

y_rk = [0.0] * y_euler.size

v_runge_kutta = [0.0] * y_euler.size

# 計算開始点に初期値をセット

y_euler[0] = y_initial

v_euler[0] = v_initial

y_rk[0] = y_initial

v_runge_kutta[0] = v_initial

計算自体はシンプルで、定義域リストの値を1つずつ進めながら、現在の値や関数への参照、パラメーターを与えてモジュールを呼び出す。

# 計算開始
for i, x in enumerate(x_calc):
    # Euler法
    (y_euler[i + 1], v_euler[i + 1]) = \
        diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx,
                      func=derivative, params=params)
    # Runge-Kutta法
    (y_rk[i + 1], v_runge_kutta[i + 1]) = \
        diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx,
                            func=derivative, params=params)

# 計算開始

for i, x in enumerate(x_calc):

# Euler法

(y_euler[i + 1], v_euler[i + 1]) = \

diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx,

func=derivative, params=params)

# Runge-Kutta法

(y_rk[i + 1], v_runge_kutta[i + 1]) = \

diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx,

func=derivative, params=params)

実行例

元の解析解と併せて表示した実行結果は以下の通りで、1回微分方程式の場合と同じく、Euler法の解は計算が進むごとに乖離が大きくなっている。Runge-Kutta法の解はかなり正確に解析解と一致している。

以下は、解析解も含めてグラフ表示するための、全体の実行コード。

# 放物線の1階常微分方程式

import numpy as np
import matplotlib.pyplot as plt
import diffeq

# 解析解を計算する関数
def y_calc(x, a):
    return a * x**2

# 微分方程式の右辺の関数
def derivative(x, y, v, a):
    return 2 * a

# 関数に渡すパラメーター
params = {'a': 1.0}

# 計算に必要な値の設定
x_start = -1.0  # 計算開始点のxの値
x_end = 1.0     # 計算終了点のxの値
dx = 0.1        # 分割幅
y_initial = 1.0 # 計算開始点におけるyの初期値
v_initial = -2.0# 計算開始点におけるvの値

# 以下、計算用リストの確保
# 計算点数
num_points = int((x_end - x_start) / dx) + 1
# for分で回すためのxのリスト
# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない
x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)
# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)
y_euler = np.linspace(x_start, x_end, num=num_points)
v_euler = [0.0] * y_euler.size
y_rk = [0.0] * y_euler.size
v_runge_kutta = [0.0] * y_euler.size

# 計算開始点に初期値をセット
y_euler[0] = y_initial
v_euler[0] = v_initial
y_rk[0] = y_initial
v_runge_kutta[0] = v_initial

# 比較用の解析解表示のための定義域と計算値
x_domain = np.linspace(x_start, x_end, num=num_points)
y = y_calc(x=x_domain, a=params['a'])

# 計算開始
for i, x in enumerate(x_calc):
    # Euler法
    (y_euler[i + 1], v_euler[i + 1]) = \
        diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx,
                      func=derivative, params=params)
    # Runge-Kutta法
    (y_rk[i + 1], v_runge_kutta[i + 1]) = \
        diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx,
                            func=derivative, params=params)

# グラフ描画
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(x_domain, y, label="Solution", color="blue", linestyle="dashed", linewidth=4)
ax.plot(x_domain, y_euler, label="Euler", color="green", linestyle="solid", linewidth=2)
ax.plot(x_domain, y_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)
ax.set_aspect('equal')
ax.text(0, 1, 'dx=' + str(dx))
ax.legend(loc="upper right")
plt.show()

# 放物線の1階常微分方程式

import numpy as np

import matplotlib.pyplot as plt

import diffeq

# 解析解を計算する関数

def y_calc(x, a):

return a * x**2

# 微分方程式の右辺の関数

def derivative(x, y, v, a):

return 2 * a

# 関数に渡すパラメーター

params = {'a': 1.0}

# 計算に必要な値の設定

x_start = -1.0 # 計算開始点のxの値

x_end = 1.0 # 計算終了点のxの値

dx = 0.1 # 分割幅

y_initial = 1.0 # 計算開始点におけるyの初期値

v_initial = -2.0# 計算開始点におけるvの値

# 以下、計算用リストの確保

# 計算点数

num_points = int((x_end - x_start) / dx) + 1

# for分で回すためのxのリスト

# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない

x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)

# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)

y_euler = np.linspace(x_start, x_end, num=num_points)

v_euler = [0.0] * y_euler.size

y_rk = [0.0] * y_euler.size

v_runge_kutta = [0.0] * y_euler.size

# 計算開始点に初期値をセット

y_euler[0] = y_initial

v_euler[0] = v_initial

y_rk[0] = y_initial

v_runge_kutta[0] = v_initial

# 比較用の解析解表示のための定義域と計算値

x_domain = np.linspace(x_start, x_end, num=num_points)

y = y_calc(x=x_domain, a=params['a'])

# 計算開始

for i, x in enumerate(x_calc):

# Euler法

(y_euler[i + 1], v_euler[i + 1]) = \

diffeq.euler2(x=x, y=y_euler[i], v=v_euler[i], dx=dx,

func=derivative, params=params)

# Runge-Kutta法

(y_rk[i + 1], v_runge_kutta[i + 1]) = \

diffeq.rk4_2(x=x, y=y_rk[i], v=v_runge_kutta[i], dx=dx,

func=derivative, params=params)

# グラフ描画

fig, ax = plt.subplots(figsize=(12, 6))

ax.plot(x_domain, y, label="Solution", color="blue", linestyle="dashed", linewidth=4)

ax.plot(x_domain, y_euler, label="Euler", color="green", linestyle="solid", linewidth=2)

ax.plot(x_domain, y_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)

ax.set_aspect('equal')

ax.text(0, 1, 'dx=' + str(dx))

ax.legend(loc="upper right")

plt.show()

1階常微分方程式の数値解法

2023-06-24 / tau / コメントする

概要

1階常微分方程式の数値解法、Euler法とRunge-Kutta法をPythonのモジュールとしてまとめた。

2階常微分方程式の解法についてはこちら。

基本形

以下のような方程式を考える。

(1) $\begin{equation*} \dfrac{dy}{dx} = y' = f(x, y, ...) \end{equation*}$

Euler法

Euler法はシンプルな方法で、ある計算ステップiの時の関数上の点(x_i, y_i)とその点における微分係数y‘_iを使って、計算幅dxだけ先にある点x_i+1 = x_i + dxのに対応するy_iの値を近似的に計算する。

(2) $\begin{align*} \Delta y_i &= \Delta x \cdot f(x_i, y_i, ...) \\ x_{i+1} &= x_i + \Delta x \\ y_{i+1} &= y_i + \Delta y_i \end{align*}$

概念図からもわかるように、たとえば下に凸の関数の場合、微分係数で線形的に予測した値は常に真値より小さくなるため、誤差が拡大していくことが予想される。

Runge-Kutta法

Runge-Kutta法には1次、2次など異なる次数の解法があるが、4次の方法がよく紹介されている。

(3) $\begin{align*} \Delta y_{1, i} &= \Delta x \cdot f(x_i, y_i, ...) \\ \Delta y_{2, i} &= \Delta x \cdot f \left ( x_i + \dfrac{\Delta x}{2}, y_i + \dfrac{\Delta y_{1, i}}{2}, ... \right ) \\ \Delta y_{3, i} &= \Delta x \cdot f \left ( x_i + \dfrac{\Delta x}{2}, y_i + \dfrac{\Delta y_{2, i}}{2}, ... \right ) \\ \Delta y_{4, i} &= \Delta x \cdot f(x_i + \Delta x, y_i + \Delta y_{3, i}, ...) \\ x_{i+1} &= x_i + \Delta x \\ y_{i+1} &= y_i + \frac{\Delta y_{1, i} + 2 \Delta y_{2, i} + 2 \Delta y_{3, i} + \Delta y_{4, i}}{6} \end{align*}$

これを説明するのに、x–y平面上での関数を描き、その微分係数を複数描いているものが多い。

本来は、右辺のz = f(…)上のある曲線があって、それをx–y平面に投影した曲線のある点における微分係数と、その点におけるzの値が等しくなるような曲線を求めるという意味となる。実際にzの値と投影曲線の微分係数が等しいというのを直感的に示すのはやっかいだなと思っていた。

いろいろ探してみると、どうやらこの式形は元の関数をTaylor展開して、次数を上げて精度を高めるというものらしい。文献を見てみると、その導出過程でかなり長々とした式が出ていた。時間がある時に試してみたい。

数値解法モジュール

コード

Euler法とRunge-Kutta法で1階常微分方程式を解くモジュールを、Pythonで以下の様に書いた。

# 1階常微分方程式
# - y' = f(x, y, ...)の形の方程式が対象
# - ある計算ステップのx(i), y(i)を与え、次のステップのy(i+1)の値を返す
# - 呼び出し側で、右辺f=func(x, y, param1, param2, ...)のように定義されている必要がある
# 使用例
# - dy/dt = derivative(x, y, param1, param2)の場合
# - params = {'param1': 2.0, 'param2': 3.14}のようにパラメーターを定義
# - 以下のように呼び出して、ステップ計算を進める
# - y_next = euler1(x=x_now, y=y_now, derivative, params)あるいは
# - y_next = rk4_1(x=x_now, y=y_now, derivative, params)
# funcに与える関数がパラメータを持たない場合、上の引数でparams=Noneを指定

# Euler法により1階常微分微分方程式を解く
def euler1(x, y, dx, func, params):
    if params is None:
        return y + dx * func(x=x, y=y)
    else:
        return y + dx * func(x=x, y=y, **params)

# 4次のRunge-Kutta法により1階常微分方程式を解く
def rk4_1(x, y, dx, func, params):
    if params is None:
        dy1 = dx * func(x=x, y=y)
        dy2 = dx * func(x=x+dx/2, y=y+dy1/2)
        dy3 = dx * func(x=x+dx/2, y=y+dy2/2)
        dy4 = dx * func(x+dx, y+dy3)
        return y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6
    else:
        dy1 = dx * func(x=x, y=y, **params)
        dy2 = dx * func(x=x+dx/2, y=y+dy1/2, **params)
        dy3 = dx * func(x=x+dx/2, y=y+dy2/2, **params)
        dy4 = dx * func(x+dx, y+dy3, **params)
        return y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6

# 1階常微分方程式

# - y' = f(x, y, ...)の形の方程式が対象

# - ある計算ステップのx(i), y(i)を与え、次のステップのy(i+1)の値を返す

# - 呼び出し側で、右辺f=func(x, y, param1, param2, ...)のように定義されている必要がある

# 使用例

# - dy/dt = derivative(x, y, param1, param2)の場合

# - params = {'param1': 2.0, 'param2': 3.14}のようにパラメーターを定義

# - 以下のように呼び出して、ステップ計算を進める

# - y_next = euler1(x=x_now, y=y_now, derivative, params)あるいは

# - y_next = rk4_1(x=x_now, y=y_now, derivative, params)

# funcに与える関数がパラメータを持たない場合、上の引数でparams=Noneを指定

# Euler法により1階常微分微分方程式を解く

def euler1(x, y, dx, func, params):

if params is None:

return y + dx * func(x=x, y=y)

else:

return y + dx * func(x=x, y=y, **params)

# 4次のRunge-Kutta法により1階常微分方程式を解く

def rk4_1(x, y, dx, func, params):

if params is None:

dy1 = dx * func(x=x, y=y)

dy2 = dx * func(x=x+dx/2, y=y+dy1/2)

dy3 = dx * func(x=x+dx/2, y=y+dy2/2)

dy4 = dx * func(x+dx, y+dy3)

return y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6

else:

dy1 = dx * func(x=x, y=y, **params)

dy2 = dx * func(x=x+dx/2, y=y+dy1/2, **params)

dy3 = dx * func(x=x+dx/2, y=y+dy2/2, **params)

dy4 = dx * func(x+dx, y+dy3, **params)

return y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6

関数euler1、rk4_1の使い方はいずれも同じで、以下の通り。

x, y：現在の計算ステップでの独立変数xと関数値yの値
dx：計算の分割幅
func：微分方程式の右辺の関数
params：関数funcに与えるパラメーター

戻り値は実数型の数値。

使い方

モジュールの使い方の概要は以下のとおり。

右辺の関数を定義する
関数に渡すパラメーターを設定する
計算開始点と終了点のxの値、分割幅dx, yの初期値を設定する
x, yの計算用リストを確保する
計算開始点のyのリストに初期値をセットする
計算実行

単純な放物線の微分方程式を例にしてモジュールの使い方を示す。まず、解の方程式として以下を考える。

(4) $\begin{equation*} y = a x^2 \quad (-1 \le x \le 1) \end{equation*}$

この式を1階微分した、以下の常微分方程式を解いていく。

(5) $\begin{equation*} y'= 2ax \quad (x = -1 \Rightarrow y = 1) \end{equation*}$

まず、必要なパッケージをインポート。diffeqは上で示したモジュールを収めている。

import numpy as np
import matplotlib.pyplot as plt
import diffeq

import numpy as np

import matplotlib.pyplot as plt

import diffeq

# 微分方程式の右辺の関数
def derivative(x, y, a):
    return 2 * a * x

# 関数に渡すパラメーター
params = {'a': 1.0}

# 微分方程式の右辺の関数

def derivative(x, y, a):

return 2 * a * x

# 関数に渡すパラメーター

params = {'a': 1.0}

数値計算に計算開始点x_startと終了点x_end、分割幅dx、yの計算初期値を設定。

# 計算に必要な値の設定
x_start = -1.0  # 計算開始点のxの値
x_end = 1.0     # 計算終了点のxの値
dx = 0.2        # 分割幅
y_initial = 1.0 # 計算開始点におけるyの初期値

# 計算に必要な値の設定

x_start = -1.0 # 計算開始点のxの値

x_end = 1.0 # 計算終了点のxの値

dx = 0.2 # 分割幅

y_initial = 1.0 # 計算開始点におけるyの初期値

次に、予めxの計算点のリストを用意して、これに対応するyの値を計算・保存していく。計算点数は植木算で分割数＋1とし、ループ計算に用いるリストは計算終了点を除いている。結果を保存しないなら、リストではなく逐次各ステップの計算値を次のステップの入力値にする。

また、計算開始点におけるyの初期値をセットしている。

# 以下、計算用リストの確保
# 計算点数
num_points = int((x_end - x_start) / dx) + 1
# for分で回すためのxのリスト
# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない
x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)
# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)
y_euler = np.linspace(x_start, x_end, num=num_points)
y_rk = [0.0] * y_euler.size

# 計算開始点に初期値をセット
y_euler[0] = y_initial
y_rk[0] = y_initial

# 以下、計算用リストの確保

# 計算点数

num_points = int((x_end - x_start) / dx) + 1

# for分で回すためのxのリスト

# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない

x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)

# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)

y_euler = np.linspace(x_start, x_end, num=num_points)

y_rk = [0.0] * y_euler.size

# 計算開始点に初期値をセット

y_euler[0] = y_initial

y_rk[0] = y_initial

計算自体はシンプルで、定義域リストの値を1つずつ進めながら、現在の値や関数への参照、パラメーターを与えてモジュールを呼び出す。

# 計算開始
for i, x in enumerate(x_calc):
    # Euler法
    y_euler[i + 1] = \
        diffeq.euler1(x=x, y=y_euler[i], dx=dx, func=derivative, params=params)
    # Runge-Kutta法
    y_rk[i + 1] = \
        diffeq.rk4_1(x=x, y=y_rk[i], dx=dx, func=derivative, params=params)

# 計算開始

for i, x in enumerate(x_calc):

# Euler法

y_euler[i + 1] = \

diffeq.euler1(x=x, y=y_euler[i], dx=dx, func=derivative, params=params)

# Runge-Kutta法

y_rk[i + 1] = \

diffeq.rk4_1(x=x, y=y_rk[i], dx=dx, func=derivative, params=params)

実行例

元の解析解と併せて表示した実行結果は以下の通りで、予想通りEuler法の解は計算が進むごとに乖離が大きくなっている。Runge-Kutta法の解はかなり正確に解析解と一致している。

以下は、解析解も含めてグラフ表示するための、全体の実行コード。

# 放物線の1階常微分方程式

import numpy as np
import matplotlib.pyplot as plt
import diffeq

# 解析解を計算する関数
def y_calc(x, a):
    return a * x**2

# 微分方程式の右辺の関数
def derivative(x, y, a):
    return 2 * a * x

# 関数に渡すパラメーター
params = {'a': 1.0}

# 計算に必要な値の設定
x_start = -1.0  # 計算開始点のxの値
x_end = 1.0     # 計算終了点のxの値
dx = 0.1        # 分割幅
y_initial = 1.0 # 計算開始点におけるyの初期値

# 以下、計算用リストの確保
# 計算点数
num_points = int((x_end - x_start) / dx) + 1
# for分で回すためのxのリスト
# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない
x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)
# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)
y_euler = np.linspace(x_start, x_end, num=num_points)
y_rk = [0.0] * y_euler.size

# 計算開始点に初期値をセット
y_euler[0] = y_initial
y_rk[0] = y_initial

# 比較用の解析解表示のための定義域と計算値
x_domain = np.linspace(x_start, x_end, num=num_points)
y = y_calc(x=x_domain, a=params['a'])

# 計算開始
for i, x in enumerate(x_calc):
    # Euler法
    y_euler[i + 1] = \
        diffeq.euler1(x=x, y=y_euler[i], dx=dx, func=derivative, params=params)
    # Runge-Kutta法
    y_rk[i + 1] = \
        diffeq.rk4_1(x=x, y=y_rk[i], dx=dx, func=derivative, params=params)

# グラフ描画
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(x_domain, y, label="Solution", color="blue", linestyle="dashed", linewidth=4)
ax.plot(x_domain, y_euler, label="Euler", color="green", linestyle="solid", linewidth=2)
ax.plot(x_domain, y_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)
ax.set_aspect('equal')
ax.text(0, 1, 'dx=' + str(dx))
ax.legend(loc="upper right")
plt.show()

# 放物線の1階常微分方程式

import numpy as np

import matplotlib.pyplot as plt

import diffeq

# 解析解を計算する関数

def y_calc(x, a):

return a * x**2

# 微分方程式の右辺の関数

def derivative(x, y, a):

return 2 * a * x

# 関数に渡すパラメーター

params = {'a': 1.0}

# 計算に必要な値の設定

x_start = -1.0 # 計算開始点のxの値

x_end = 1.0 # 計算終了点のxの値

dx = 0.1 # 分割幅

y_initial = 1.0 # 計算開始点におけるyの初期値

# 以下、計算用リストの確保

# 計算点数

num_points = int((x_end - x_start) / dx) + 1

# for分で回すためのxのリスト

# n-1ステップの計算が最後でnステップ目のyを計算するため、xの終了点は含まない

x_calc = np.linspace(x_start, x_end, num=num_points-1, endpoint=False)

# Euler法・Runge-Kutta法の数値解yの保存領域(終了点を含む)

y_euler = np.linspace(x_start, x_end, num=num_points)

y_rk = [0.0] * y_euler.size

# 計算開始点に初期値をセット

y_euler[0] = y_initial

y_rk[0] = y_initial

# 比較用の解析解表示のための定義域と計算値

x_domain = np.linspace(x_start, x_end, num=num_points)

y = y_calc(x=x_domain, a=params['a'])

# 計算開始

for i, x in enumerate(x_calc):

# Euler法

y_euler[i + 1] = \

diffeq.euler1(x=x, y=y_euler[i], dx=dx, func=derivative, params=params)

# Runge-Kutta法

y_rk[i + 1] = \

diffeq.rk4_1(x=x, y=y_rk[i], dx=dx, func=derivative, params=params)

# グラフ描画

fig, ax = plt.subplots(figsize=(12, 6))

ax.plot(x_domain, y, label="Solution", color="blue", linestyle="dashed", linewidth=4)

ax.plot(x_domain, y_euler, label="Euler", color="green", linestyle="solid", linewidth=2)

ax.plot(x_domain, y_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2)

ax.set_aspect('equal')

ax.text(0, 1, 'dx=' + str(dx))

ax.legend(loc="upper right")

plt.show()

放物線の焦点

2023-06-23 / tau / コメントする

概要

放物線が、その対称軸に平行な線に対して焦点を持つことを確認する。イメージ図は以下の通り。

証明

下図を考える。

放物線Cを以下の式で定義する。

(1) $\begin{equation*} C: \: y_0(x) = a x^2 \end{equation*}$

任意の点(X, Y)における接線l₁の式は以下の様になる。

(2) $\begin{align*} l_1: \: y_1(x) &= y_1' (X) \cdot (x - X) + Y &= 2aX (x - X) + X^2 \end{align*}$

ここで、y₁‘は、図中の角θを用いて以下のように表せる。

(3) $\begin{equation*} y_1'(X) = \tan \theta \quad \left( -\frac{\pi}{2} \le \theta < \frac{\pi}{2} \right) \end{equation*}$

また、この点を通ってl₁に垂直な直線l₂の式は、この点におけるl2の微分係数をy₂‘として以下のように表せる。

(4) $\begin{equation*} l_2: \: y_2(x) = y_2' (X) \cdot (x - X) + Y \end{equation*}$

ここでy₂‘は、図中の角θを用いて以下のように導かれる。

(5) $\begin{align*} y_2'(X) &= - \tan \left( \dfrac{\pi}{2} - 2 \theta \right) \\ &= - \frac{\cos 2 \theta}{\sin 2 \theta} \\ &= - \frac{\cos^2 \theta - \sin^2 \theta}{2 \sin \theta \cos \theta} \\ &= - \frac{-1 + \tan^2 \theta}{2 \tan \theta} \end{align*}$

この式でθがπ/2よりも大きい場合でも、式形は変わらない。

ここで式(3)を考慮して、l₂の式は以下のように変形される。

(6) $\begin{equation*} y_2(x) = \frac{-1 + 4 a^2 X^2}{4aX} (x - X) + a X^2 \end{equation*}$

l₂がy軸と交わる点のy座標値を求める。

(7) $\begin{align*} y_2(0) &= \frac{-1 + 4 a^2 X^2}{4aX} (-X) + a X^2 \\ &= \frac{X - 4 a^2 X^3 + 4a^2 X^3}{4aX} \\ &= \frac{1}{4a} \end{align*}$

この値はXに寄らず一定なことから、y軸に平行な線が放物線で反射された線は、y軸上の1点を通る。

なお、入射線と反射線が直角になるときの入射線のx座標値は以下の通り。

(8) $\begin{align*} a x^2 = \frac{1}{4a} \quad \Leftrightarrow \quad x = \plusminus \frac{1}{2a} \end{align*}$

斜め入射について

たとえば先の図で、入射角が右側に傾いた場合を考える。

y軸の右側（xが正の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより浅くなることから、反射方向はより下側に傾く。したがって、反射線とy軸の交点は下側に移動する。

一方y軸の左側（xが負の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより深くなることから、反射方向はより上側に傾く。したがって、反射線とy軸の交点は上側に移動する。

少なくともy軸の両側で反射線のy軸との交点が一致しないことから、焦点は存在しない。より正確には、入射線のy軸に対する傾きをαなどと置いて上記のような計算をするとよい。

PythonCGI – 基本

2023-03-30 / tau / コメントする

概要

PythonのコードでCGI(Common Gateway Interface)によってHTMLをする方法の基本。

基本の枠組み

コード例

例えば以下の内容をindex.pyとして準備。

SheBangでPythonの場所を指定
Content-Typeを出力して1行空ける
出力内容を記述

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('Python CGI Test')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('Python CGI Test')

HTTPのヘッダーで最低限Content-Typeを出力し、ボディーとの間に空行が1行必要。これがないと、500エラーとなり、ログには以下の様に記録される。

[cgi:error] [pid 30090] [client 192.168.33.1:65449] malformed header from script 'index.py': Bad header: Python CGI Test

1	[cgi:error] [pid 30090] [client 192.168.33.1:65449] malformed header from script 'index.py': Bad header: Python CGI Test

コードのモード確認

ファイルがrootの実行権限を持っていること。実行権限がない場合はchmod 755かchmod +xで設定する。

コードの配置

cgi実行用のディレクトリーにファイルを配置。Apacheの場合例えば/var/www/cgi-binなど。

ブラウザ表示

URLで[ホスト]/cgi-bin/index.pyを指定すると、ブラウザーにPython CGI Testと表示される。

HTML出力例

ASCII出力

基本の枠組みの出力に、以下の様にタグを加えると要素として表示される。

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('<h1>Python CGI Test</h1>')
print('<p>Python CGI Test</p>')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('<h1>Python CGI Test</h1>')

print('<p>Python CGI Test</p>')

UTF-8出力

上のコードの一部を日本語にしてみる。

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('<h1>Python CGI test</h1>')
print('<p>Python CGI テスト</p>')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('<h1>Python CGI test</h1>')

print('<p>Python CGI テスト</p>')

ところがこれをブラウザーで確認すると、h1要素は表示されるがp要素が全く表示されない。ソースを確認してもh1要素の行が表示されるだけ（このコードをコンソールで実行すると、h1要素の行もp要素の行も表示される）。

これを解決するには、ソースコードでio.TextIOWrapperを実行するとよいらしい。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

print('Content-Type: text/html')
print('')
print('<h1>Python CGI test</h1>')
print('<p>Python CGI テスト</p>')

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

print('Content-Type: text/html')

print('')

print('<h1>Python CGI test</h1>')

print('<p>Python CGI テスト</p>')

上記の2行を追加すると、無事日本語まで表示された。

HTML出力

コンテンツを以下の様にHTMLの構造にして出力する。title要素も機能して、タブの表示が変更された。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html = '''
<html>
    <head>
        <title>Python CGI</title>
    </head>
    <body>
        <h1>Python CGI test</h1>
        <p>Python CGI HTMLテスト</p>
    </body>
</html>
'''

print('Content-Type: text/html')
print('')
print(html)

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html = '''

<html>

<head>

<title>Python CGI</title>

</head>

<body>

<h1>Python CGI test</h1>

<p>Python CGI HTMLテスト</p>

</body>

</html>

'''

print('Content-Type: text/html')

print('')

print(html)

ループの利用例

以下のコードでは、見栄えは良くないがforループでli要素を生成している。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html_head = '''
<head>
    <title>Python CGI</title>
</head>
'''

html_body = '''
<h1>Python CGI test</h1>
<p>Python CGI HTMLテスト</p>
'''

print('Content-Type: text/html')
print('')
print('<html>')
print(html_head)
print('<body>')
print(html_body)
print('<ol>')
for i in range(5):
    print('<li>{}番目のli要素</li>'.format(i + 1))
print('</ol>')
print('</body')
print('</html>')

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html_head = '''

<head>

<title>Python CGI</title>

</head>

'''

html_body = '''

<h1>Python CGI test</h1>

<p>Python CGI HTMLテスト</p>

'''

print('Content-Type: text/html')

print('')

print('<html>')

print(html_head)

print('<body>')

print(html_body)

print('<ol>')

for i in range(5):

print('<li>{}番目のli要素</li>'.format(i + 1))

print('</ol>')

print('</body')

print('</html>')

出力に以下が加わる。

1番目のli要素
2番目のli要素
3番目のli要素
4番目のli要素
5番目のli要素

Apacheの設定

今回は/etc/httpd/conf/httpd.confのデフォルトのままでcgi-scriptの設定を加えていないが、そのままで適切に実行された。

2次元リストの結合

2023-01-28 / tau / コメントする

概要

2次元リスト同士の結合について整理。

縦方向の結合
- appendはループが必要
- extendは破壊的に結合
- ＋演算子は非破壊的に結合
横方向の結合
- extendでループが必要
- ＋演算子はループの方法に注意

縦方向の結合

appendは要注意

1次元のリストの場合と同じく、appendは引数全体を要素として追加してしまう。

a = [
    [1, 2],
    [3, 4]
]

b = [
    [5, 6],
    [7, 8]
]

a.append(b)

print(a)
print(b)

# [[1, 2], [3, 4], [[5, 6], [7, 8]]]
# [[5, 6], [7, 8]]

a = [

[1, 2],

[3, 4]

]

b = [

[5, 6],

[7, 8]

]

a.append(b)

print(a)

print(b)

# [[1, 2], [3, 4], [[5, 6], [7, 8]]]

# [[5, 6], [7, 8]]

追加されるリストの各行を取り出して追加すれば可能。ただし破壊的。

for r in b:
    a.append(r)

print(a)
print(b)

# [[1, 2], [3, 4], [5, 6], [7, 8]]
# [[5, 6], [7, 8]]

for r in b:

a.append(r)

print(a)

print(b)

# [[1, 2], [3, 4], [5, 6], [7, 8]]

# [[5, 6], [7, 8]]

extendはok（破壊的）

extendは引数のリストの内容をそのまま追加してくれる。ただし破壊的。

a = [
    [1, 2],
    [3, 4]
]

b = [
    [5, 6],
    [7, 8]
]

a.extend(b)

print(a)
print(b)

# [[1, 2], [3, 4], [5, 6], [7, 8]]
# [[5, 6], [7, 8]]

a = [

[1, 2],

[3, 4]

]

b = [

[5, 6],

[7, 8]

]

a.extend(b)

print(a)

print(b)

# [[1, 2], [3, 4], [5, 6], [7, 8]]

# [[5, 6], [7, 8]]

＋演算子もok（非破壊的）

＋演算子もextendと同じ挙動だが非破壊的。

a = [
    [1, 2],
    [3, 4]
]

b = [
    [5, 6],
    [7, 8]
]

c = a + b

print(a)
print(b)
print(c)

# [[1, 2], [3, 4]]
# [[5, 6], [7, 8]]
# [[1, 2], [3, 4], [5, 6], [7, 8]]

a = [

[1, 2],

[3, 4]

]

b = [

[5, 6],

[7, 8]

]

c = a + b

print(a)

print(b)

print(c)

# [[1, 2], [3, 4]]

# [[5, 6], [7, 8]]

# [[1, 2], [3, 4], [5, 6], [7, 8]]

横方向の結合

extendで一手間必要

extendで各要素に追加する場合、各要素をループで取出して追加する必要がある。

a = [
    [1, 2],
    [3, 4]
]

b = [
    [5, 6],
    [7, 8]
]

for i in range(len(a)):
    a[i].extend(b[i])

print(a)
print(b)

# [[1, 2, 5, 6], [3, 4, 7, 8]]
# [[5, 6], [7, 8]]

a = [

[1, 2],

[3, 4]

]

b = [

[5, 6],

[7, 8]

]

for i in range(len(a)):

a[i].extend(b[i])

print(a)

print(b)

# [[1, 2, 5, 6], [3, 4, 7, 8]]

# [[5, 6], [7, 8]]

カウンターではなく要素を直接取り出してもok。

for ra, rb in zip(a, b):
    ra.extend(rb)

print(a)
print(b)

# [[1, 2], [3, 4]]
# [[5, 6], [7, 8]]

for ra, rb in zip(a, b):

ra.extend(rb)

print(a)

print(b)

# [[1, 2], [3, 4]]

# [[5, 6], [7, 8]]

＋演算子は要注意

＋演算子で結合する場合は、結果のリストを準備しておく必要がある。このとき、結合するリストと同じ要素数（行数）の空のリストを要素に持つリストを準備しておく必要がある。

また、ループはカウンターを使って添字でリスト要素を指定しなければならない。

a = [
    [1, 2],
    [3, 4]
]

b = [
    [5, 6],
    [7, 8]
]

c = [[]] * 2

for i in range(len(a)):
    c[i] = a[i] + b[i]

print(a)
print(b)
print(c)

# [[1, 2], [3, 4]]
# [[5, 6], [7, 8]]
# [[1, 2, 5, 6], [3, 4, 7, 8]]

a = [

[1, 2],

[3, 4]

]

b = [

[5, 6],

[7, 8]

]

c = [[]] * 2

for i in range(len(a)):

c[i] = a[i] + b[i]

print(a)

print(b)

print(c)

# [[1, 2], [3, 4]]

# [[5, 6], [7, 8]]

# [[1, 2, 5, 6], [3, 4, 7, 8]]

要素を直接取り出して演算した場合、変数が新たに作成されるがその結果は元のリストには反映されないので注意。

c = [[]] * 2

for ra, rb, rc in zip(a, b, c):
    rc = ra + rb

print(a)
print(b)
print(c)

# [[1, 2], [3, 4]]
# [[5, 6], [7, 8]]
# [[], []]

c = [[]] * 2

for ra, rb, rc in zip(a, b, c):

rc = ra + rb

print(a)

print(b)

print(c)

# [[1, 2], [3, 4]]

# [[5, 6], [7, 8]]

# [[], []]

リストの追加・結合

2023-01-28 / tau / コメントする

概要

リストに対する要素の追加、リストの結合について整理。

リストへの1つの要素の追加
- appendが簡明、ただし破壊的
- extendも使えるがリストとして追加、破壊的
- ＋演算子もリストとして追加、非破壊的
リスト同士の結合
- appendは使えない
- extendは破壊的にリストを追加
- ＋演算子は非破壊的にリストを追加

リストへの要素の追加

appendは破壊的

appendで1つの要素をリストに追加できる。appendは破壊的で元のリストを改変する。戻り値はNone。

x = a.append(4)

print(a)
print(x)

# [1, 2, 3, 4]
# None

x = a.append(4)

print(a)

print(x)

# [1, 2, 3, 4]

# None

appendは1つの引数しか持てない（append(4, 5)とはできない）。

extendはリストを追加（破壊的）

extendでも要素を追加できるが、要素そのものではなく、追加したい要素を含むリストとして追加する。extendは破壊的で元のリストを改変する。戻り値はNone。

a = [1, 2, 3]

x = a.extend([4])

print(a)
print(x)

# [1, 2, 3, 4]
# None

a = [1, 2, 3]

x = a.extend([4])

print(a)

print(x)

# [1, 2, 3, 4]

# None

＋演算子もリストの演算（非破壊的）

＋演算子もextendと同じくリストを追加する。extendと違って非破壊的で、元のリストは改変されず、結果は戻り値で返される。

a = [1, 2, 3]

x = a + [4]

print(a)
print(x)

# [1, 2, 3]
# [1, 2, 3, 4]

a = [1, 2, 3]

x = a + [4]

print(a)

print(x)

# [1, 2, 3]

# [1, 2, 3, 4]

リストの結合

appendは使えない

appendは引数をリストの要素として追加するので、リストを引数に与えるとそのリストが要素として追加されてしまう。

a = [1, 2, 3]
b = [4, 5, 6]

c = a.append(b)

print(a)
print(b)
print(c)

# [1, 2, 3, [4, 5, 6]]
# [4, 5, 6]
# None

a = [1, 2, 3]

b = [4, 5, 6]

c = a.append(b)

print(a)

print(b)

print(c)

# [1, 2, 3, [4, 5, 6]]

# [4, 5, 6]

# None

extendはOk（破壊的）

extendは引数に与えたリストで元のリストを拡張する。ただし破壊的で元のリストが改変される。

a = [1, 2, 3]
b = [4, 5, 6]

c = a.extend(b)

print(a)
print(b)
print(c)

# [1, 2, 3, 4, 5, 6]
# [4, 5, 6]
# None

a = [1, 2, 3]

b = [4, 5, 6]

c = a.extend(b)

print(a)

print(b)

print(c)

# [1, 2, 3, 4, 5, 6]

# [4, 5, 6]

# None

＋演算子もOk（非破壊的）

＋演算子もextendと同じくリストを拡張するが非破壊的。拡張と言うよりも、くっつける／追加するというイメージ。

a = [1, 2, 3]
b = [4, 5, 6]

c = a + b

print(a)
print(b)
print(c)

# [1, 2, 3]
# [4, 5, 6]
# [1, 2, 3, 4, 5, 6]

a = [1, 2, 3]

b = [4, 5, 6]

c = a + b

print(a)

print(b)

print(c)

# [1, 2, 3]

# [4, 5, 6]

# [1, 2, 3, 4, 5, 6]