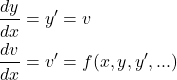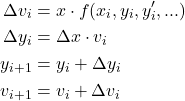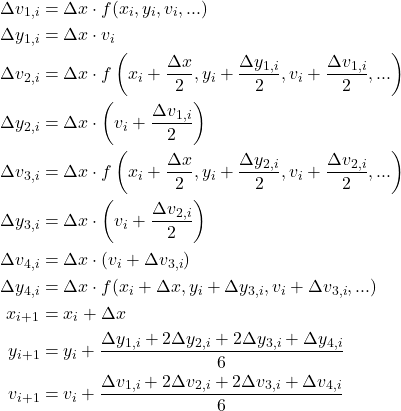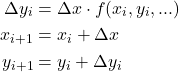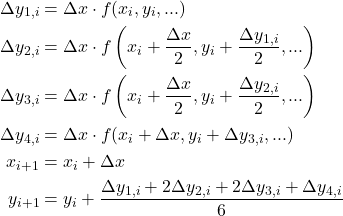概要
1階常微分方程式について、4次のRunge-Kutta法(RK4)による数値解と解析解を比較する。Euler法による解についても重ねてみた。
- RK4は、かなり粗い分割間隔でもよい結果になる
- Euler法は、分割間隔を小さくとらないと精度が上がらない
Logistic関数
方程式と解析解
Logistic関数に関する微分方程式は以下で表される。
(1) ![]()
この方程式は解析的に解けて、以下の解を得る。
(2) 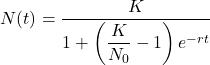
数値解
式(1)をRK4、Euler法によって解き、解析解と重ねる(解き方は1階常微分方程式の数値解法を参照)。
r=10, K=1000として計算した結果は以下の通り。
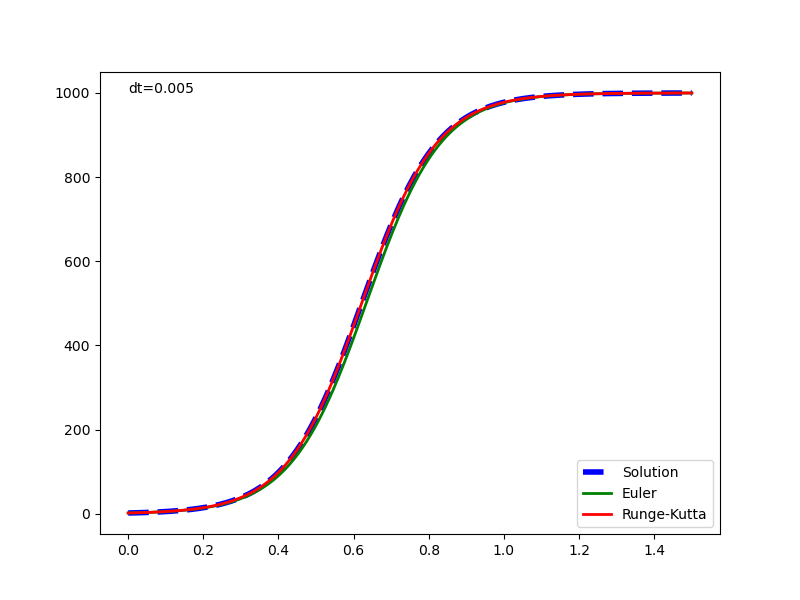
- RK4は上限に収束するまでの時間(t=1.0)の20等分くらい(dt=0.05)でもよく合っている
- Euler法では凹な部分で計算値が過少となり、凸の部分で解析解に追いついているが、適合度はよろしくない。
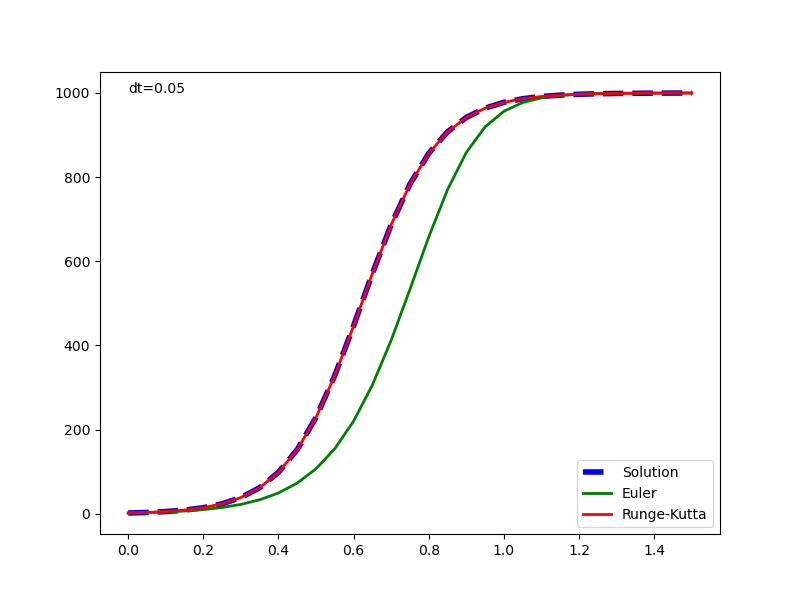
dtを上記の10分の1(dt=0.05)として計算した結果が以下の通り。Euler法もかなり適合度合いがよくなったが、それでもまだ少し右方にずれている。
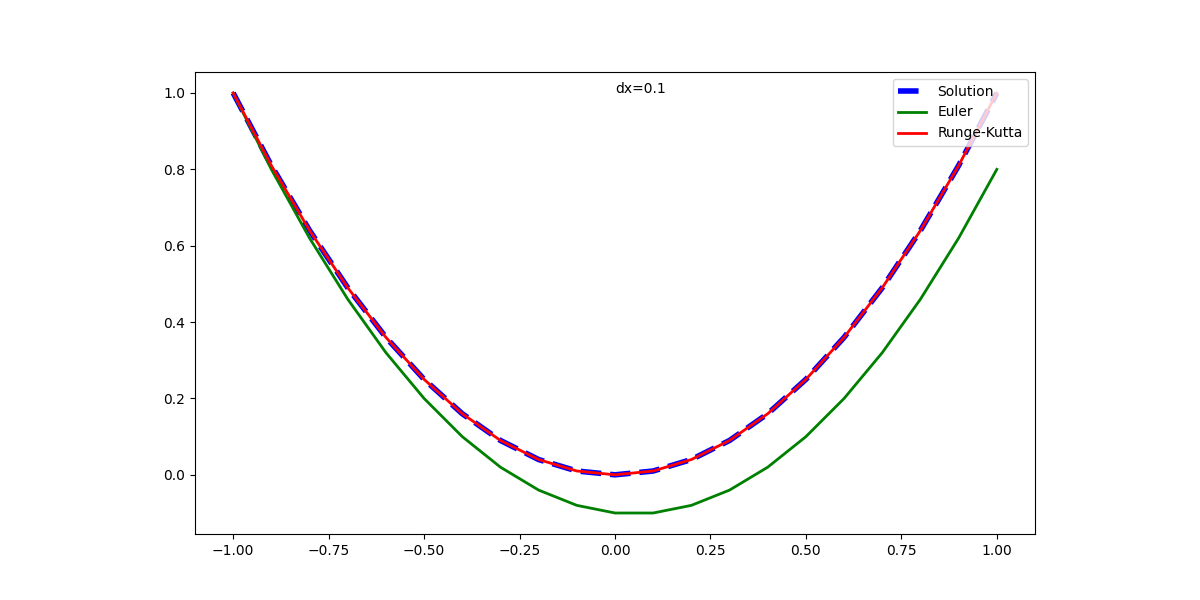
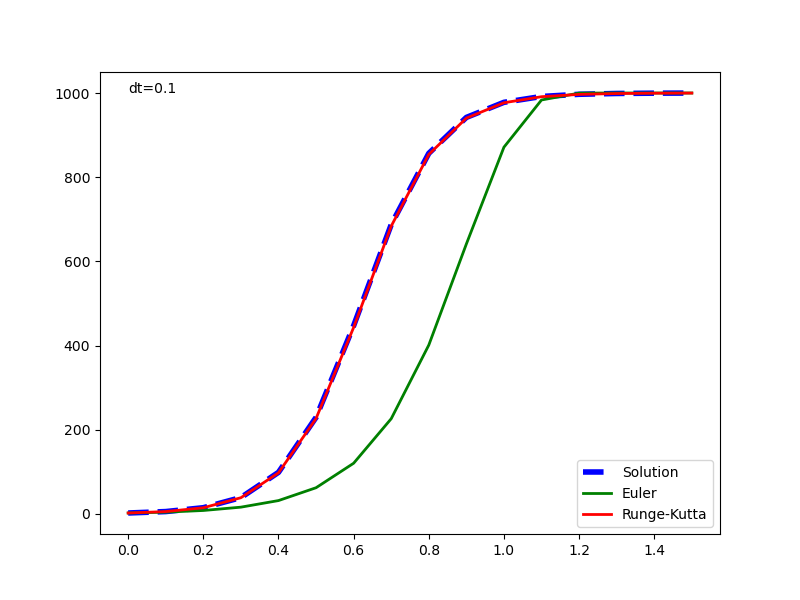
逆にdt=0.1と大きくしてみた。折れ線がはっきりわかるくらいの粗さだが、RK4はよくフィットしている。Euler法のずれは大きくなっている。
コード
上記の結果は、以下のコードを実行して得ている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# ロジスティック関数の1階常微分方程式 import numpy as np import matplotlib.pyplot as plt import diffeq # 解析解を計算する関数 def logistic(t, r, K, N_initial): return K / (1 + (K / N_initial - 1) * np.exp(-r * t)) # 微分方程式の右辺の関数 def derivative(x, y, r, K): return r * (1 - y / K) * y # 関数に渡すパラメーター params = {'r': 10, 'K': 1000} # 計算に必要な値の設定 t_start = 0 # 計算開始点のtの値 t_end = 1.5 # 計算終了点のtの値 dt = 0.05 # 分割幅 # 計算開始点におけるNの初期値をセット N_initial = 2 # 以下、計算用リストの確保 num_points = int((t_end - t_start) / dt) + 1 t_calc = np.linspace(t_start, t_end, num=num_points-1, endpoint=False) N_euler = np.linspace(t_start, t_end, num=num_points) N_rk = [0.0] * N_euler.size # 計算開始点に初期値をセット N_euler[0] = N_initial N_rk[0] = N_initial # 比較用の解析解表示のための定義域と計算値 t_domain = np.linspace(t_start, t_end, num=num_points) N_logistic = logistic(t=t_domain, N_initial=N_initial, **params) # 計算開始 for i, t in enumerate(t_calc): # Euler法 N_euler[i + 1] = diffeq.euler1( x=t, y=N_euler[i], dx=dt, func=derivative, params=params) # Runge-Kutta法 N_rk[i + 1] = diffeq.rk4_1( x=t, y=N_rk[i], dx=dt, func=derivative, params=params) # グラフ描画 fig, ax = plt.subplots(figsize=(8, 6)) ax.plot(t_domain, N_logistic, label="Solution", color="blue", linestyle="dashed", linewidth=4) ax.plot(t_domain, N_euler, label="Euler", color="green", linestyle="solid", linewidth=2) ax.plot(t_domain, N_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2) ax.text(0, params['K'], 'dt=' + str(dt)) ax.legend(loc="lower right") plt.show() |
三角関数
方程式と解析解
簡単な正弦関数を考える。
(3) ![]()
この関数は、以下の微分方程式の解である。
(4) ![]()
数値解
式(4)をEuler法、Runge-Kutta法によって解き、式(3)のグラフと重ねる。
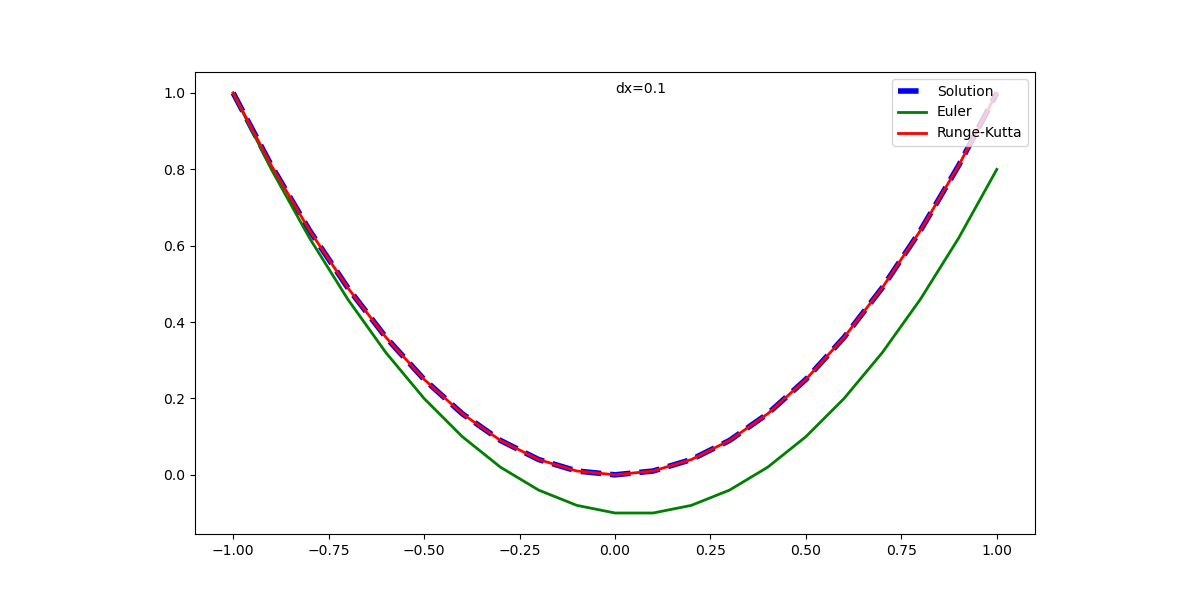
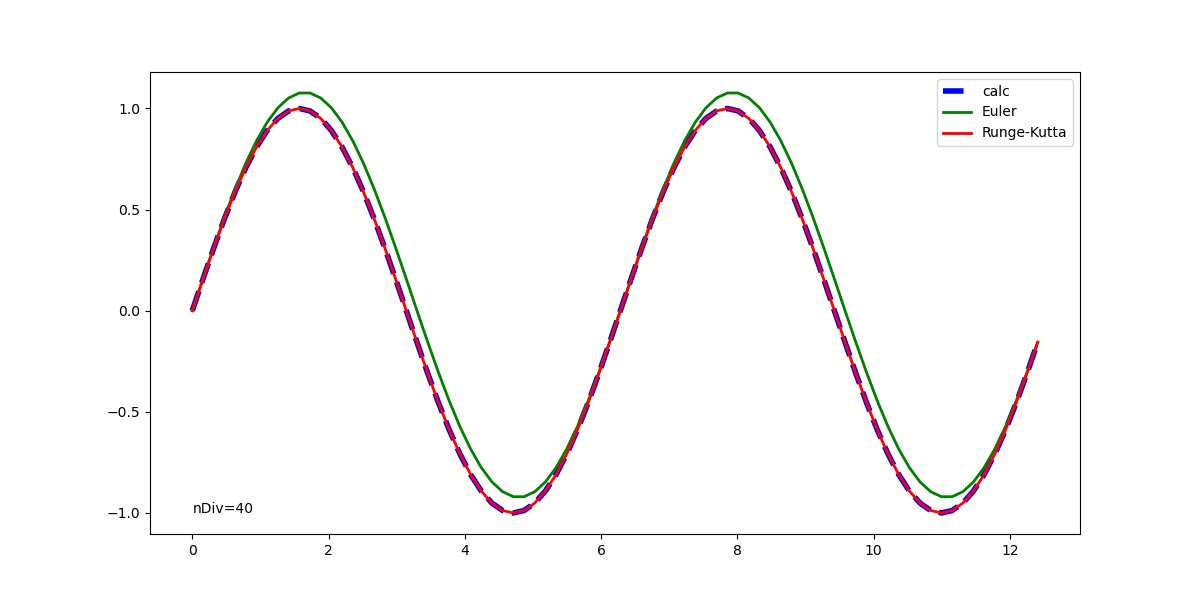
以下は分割間隔を1/40周期で計算した結果。RK4の精度はいいが、Euler法では上に凸のときに過大となり、下に凸のときに過少となって初期値に戻っている。
分割幅を1/200周期にするとEuler法でも精度は上がってくるが、まだ少し誤差が残っている。
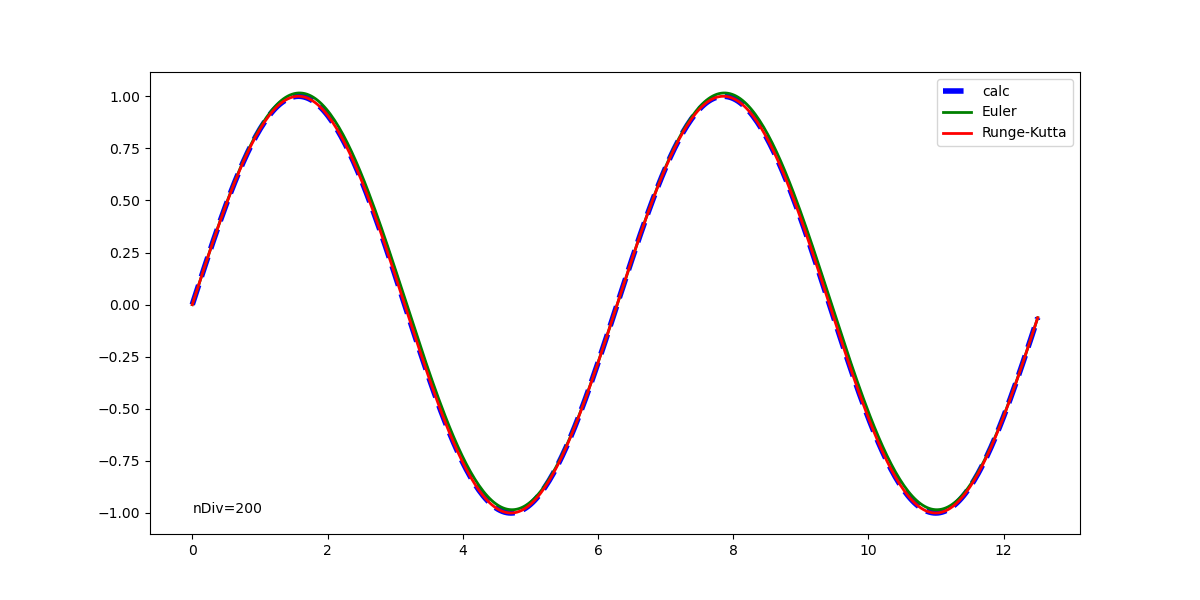
分割数を10とかなり粗くとっても、RK4の適合度合いはよい。
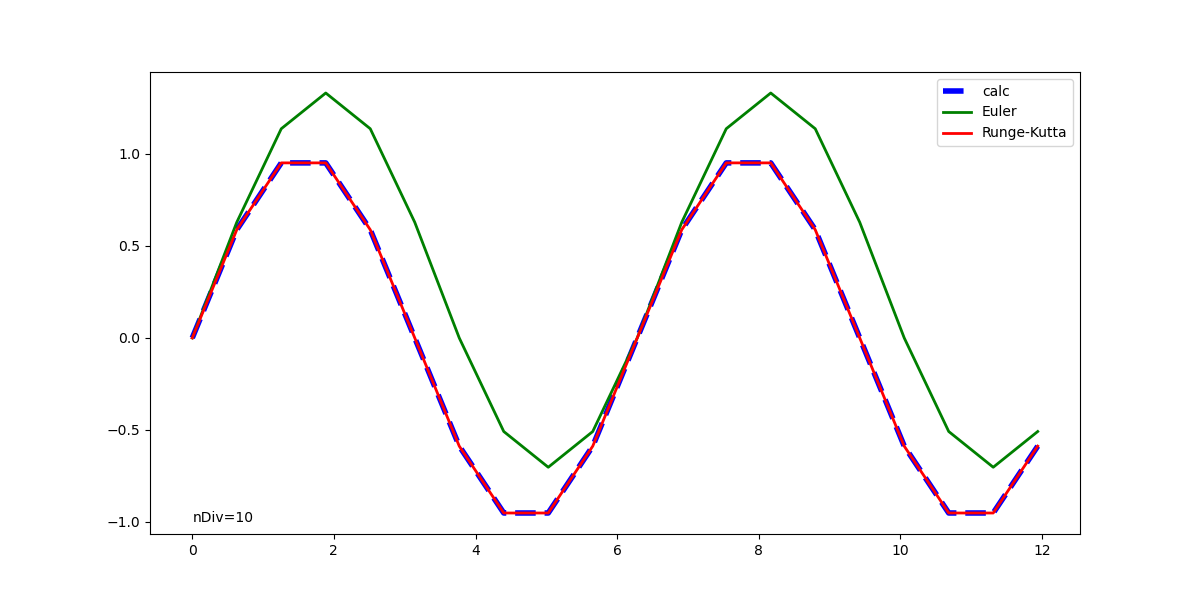
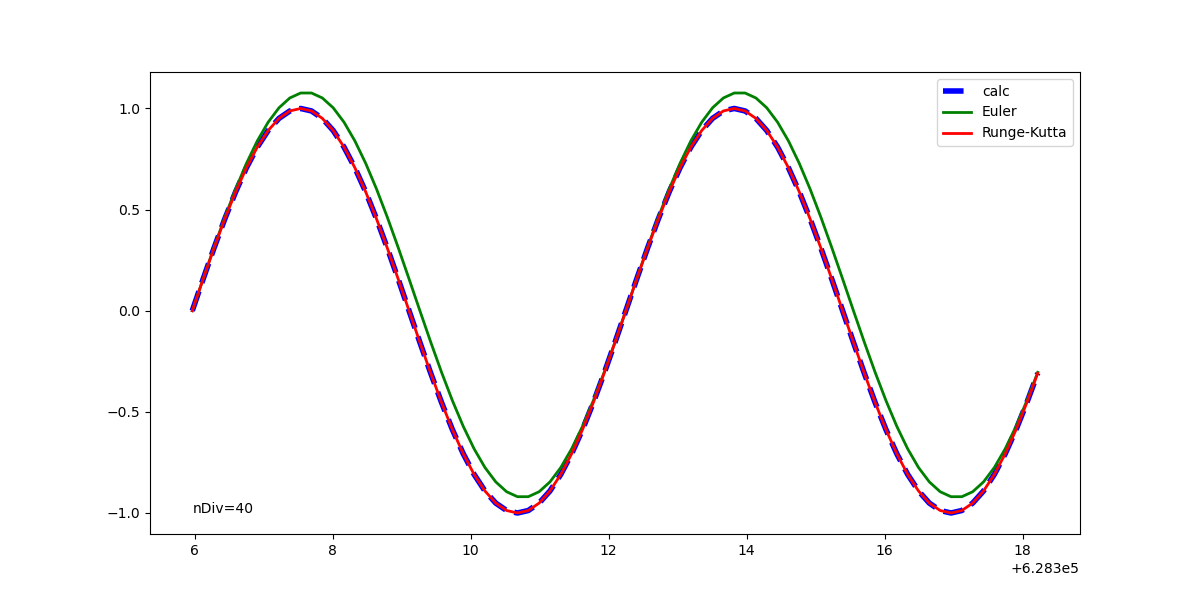
繰り返し数が増えた時に誤差が累積するかどうか確認してみた。
以下は10万周期分計算した最後の2周忌を取り出した結果で、RK4、Euler法とも傾向は変わらない。規則正しい周期関数の場合は、繰り返し数を増やしても誤差は拡散しないと思われる。
コード
以下はこれまでの計算をしたPythonのコード。
計算区間を長くとって一部だけ表示させるため、Logistic関数のときとは異なる処理をしている。
- ループの各段階で計算結果をリストに保存せず、各ステップで計算された次のステップの結果を元の変数に入れ替える
- 予め指定した計算区間の間の結果だけ、表示用のリストに保存する
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
# Runge-Kutta法で多数回計算を繰り返した際の精度を確認 # 全ての結果はリストに保存せず、必要な区間だけを保存 import numpy as np import matplotlib.pyplot as plt import diffeq # 解析解を計算する関数 def sine(x): return np.sin(t) # 微分方程式の右辺の関数 def derivative(x, y): return np.cos(x) # 計算区間と計算間隔 t_start = 0 t_end = 2 * np.pi * 100000 dt = 2 * np.pi / 40 # 表示させる区間 t_view_start = 2 * np.pi * 99998 t_view_end = 2 * np.pi * 100000 # t=0におけるyの初期値 y_initial = 0.0 # 計算点数は準備するが、繰り返し計算の答えを全部は保存しない num_points = int((t_end - t_start) / dt) + 1 # 計算開始点に初期値をセット y_now_euler = y_initial y_now_rk = y_initial # 表示する区間だけ計算結果を保存するリスト t_view = [] y_view_calc = [] y_view_euler = [] y_view_rk = [] # 計算開始 for i in range(0, num_points - 1): # iステップ目の時刻を計算 t = t_start + dt * i # 時刻が指定した区間内のときだけ配列に結果を追加 if t >= t_view_start and t <= t_view_end: t_view.append(t) y_view_calc.append(sine(t)) y_view_euler.append(y_now_euler) y_view_rk.append(y_now_rk) # i+1ステップ目の計算値 y_euler = diffeq.euler1( x=t, y=y_now_euler, dx=dt, func=derivative, params=None) y_rk = diffeq.rk4_1( x=t, y=y_now_rk, dx=dt, func=derivative, params=None) # 次のステップのため、計算結果を入れ替え y_now_euler = y_euler y_now_rk = y_rk # グラフ描画 fig, ax = plt.subplots(figsize=(12, 6)) ax.plot(t_view, y_view_calc, label="calc", color="blue", linestyle="dashed", linewidth=4) ax.plot(t_view, y_view_euler, label="Euler", color="green", linestyle="solid", linewidth=2) ax.plot(t_view, y_view_rk, label="Runge-Kutta", color="red", linestyle="solid", linewidth=2) ax.text(t_view_start, -1, 'nDiv=' + str(round(2 * np.pi / dt))) ax.legend(loc="upper right") plt.show() |