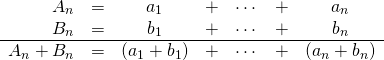概要
WordPressで整った数式を表示したいとき、MS-Officeの数式エディタの表示を画像として張り付けることを考えたが、探してみると”MathJax-LaTeX”というプラグインがよく紹介されていた。LaTexの書式で書いた数式が整形されて画像として張り付けられるらしい。
MathJax-LaTexはプラグインをインストール後、記事の冒頭にショートコード[mathjax]を書き、そのページ内でLaTexの記述が可能になという手軽なものなので、一度導入して試してみた。
ところが、ショートコードを入れたると$$マークや$マークが数式整形のための記号として認識されてしまう。たとえばjQueryに関する記事中やスクリプトコードで$マークを使うとややこしいことになる。また数式をインラインで書けないとか、テキストモードで複数行にわたる数式を書けないとか、いろいろ制約があるようだ。
そこでほかにもプラグインはないかと探して、以下のサイトに辿り着いた。
“WP QuickLaTex“というプラグインがあるそうで、試しにインストールしてみたところ悪くない。
導入手順
- プラグイン”WP QuickLaTex”をインストールし、有効化
- QuickLaTexの設定でインライン記述の$…$を無効化
- 数式を表示したい記事に以下のショートコードを書く(これにより、latexの$$記号が有効化される)
1[latexpage]
あるいは、ショートコードなしで記事中でのショートコードで囲んだ部分はQuickLaTexの認識対象になる。 - LaTex形式で数式を記述
インラインスタイル
インラインスタイル(![]() のような書き方)の場合は、以下のようにショートコードで囲む。
のような書き方)の場合は、以下のようにショートコードで囲む。
|
1 |
[latex]...[/latex] |
この機能は、冒頭にショートコードを書かなくても使える。
ディスプレイスタイル
式を別段落で表示させるディスプレイスタイルの書き方には、以下の2つの方法がある。
latexpageショートコードを書く場合
|
1 |
$$...$$ |
この場合、ショートコード以前の$$マークは無視されるが、ショートコードを書くと記事中の$$マークはQuickLaTexが数式解釈に使う。
latexpageショートコードを書かない場合
|
1 |
[latex]$$...$$[/latex] |
ディスプレイスタイルでは、上記いずれの書き方でも、テキストモードで改行して複数行にわたって記述可能。
結局現在は、ディスプレイスタイルも単に[latex]...[/latex]記号のみで書いている。
|
1 2 3 4 5 |
[latex] \begin{equation} y = a x^2 + b x + c \end{equation} [/latex] |
注意点
- $マークを設定で無効化した場合ショートコード以降の記事の中に直接$マークは書ける
- latexpageショートコード書くと記事中のの$$マークが数式解釈に使われる
- 改行文字(\\)は機能しないが、
\begin{align}~\end{align}や\begin{array}{...}~\end[array]で括ると改行される - 以下のケースではうまく表示されない
- ドルマーク2つで数式を書いた直後の行が
<pre></pre>の場合、表示されない
- ドルマーク2つで数式を書いた直後の行が
記述例
WP QuickLaTexでLaTex形式の記述がどのように表示されるか列挙する。
記号
文字
{\rm }で斜体を通常書体に、{bf }と\mathbf{}は同じで太字、{\boldmath }は機能しない。いずれもギリシャ文字(小文字)には効かない。
|
1 2 3 4 5 |
abcABC \alpha \beta \gamma \\ {\rm abcABC \alpha \beta \gamma} \\ {\bf abcABC \alpha \beta \gamma} \\ \mathbf{abcABC \alpha \beta \gamma} \\ {\boldmath ab$cABC \alpha$ \beta \gamma} |
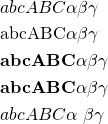
その後、\boldsymbolでアルファベットの大文字・小文字、ギリシャ文字を斜体太字にできることがわかった。
|
1 |
\boldsymbol{abcABC \alpha \beta \gamma} |
![]()
等号・不等号
|
1 2 3 4 5 |
a = 1 \\ a \neq 2 \\ a \leq 2 , \: a \leqq 2 \\ a \geq 0 . \: a \geqq 0 \\ a \sim 1.1 , \: a \simeq 1.1 , \: a \approx 1.1 , \:a \fallingdotseq 1.1 |
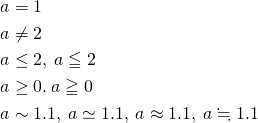
加減乗除
普通の記号
|
1 |
a + b \times c \div d |
![]()
分数
分数の記述は\fracで(分子・分母で\fracを使うと小さくなるので、元のままのサイズにしたいときは\dfracを使う
|
1 |
\frac{\frac{1}{2} + \frac{1}{2}}{\dfrac{1}{3} + \dfrac{1}{3}} |
![]()
括弧
分数などに対して背の高い括弧を使うときは、\left(、\right)などを使う。
|
1 |
\left( \frac{1}{2} + \frac{1}{3} \right) \times 6 = 5 |
![]()
ドット表記
|
1 |
z = x \cdot y |
![]()
プラス/マイナス
|
1 2 |
a \pm b a \mp b |
![]()
多項省略・ドット表記
|
1 2 3 4 |
S = 1 + 2 + \cdots + 100 S = 1 + 2 + \ldots + 100 \vdots \ddots |
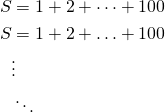
矢印
|
1 2 3 4 5 |
\leftarrow \: \Leftarrow \: \longleftarrow \: \Longleftarrow \rightarrow\ \: \Rightarrow \: \longrightarrow \: \Longrightarrow \leftrightarrow \: \Leftrightarrow \: \longleftrightarrow \: \Longleftrightarrow \uparrow \: \Uparrow \: \downarrow \: \Downarrow \nearrow \; \searrow \; \swarrow \: \nwarrow |
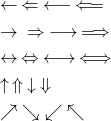
角
|
1 |
\angle R = 90^\circ |
![]()
式
基本形
latexショートコードだけで囲むと、数式が左詰めになり、式番号なしで数式が表示される。
|
1 2 3 |
[latex] z = x + y [/latex] |
![]()
equation環境では、数式がセンタリングされ、式番号が付けられる。
|
1 2 3 4 5 |
[latex] \begin{equation} z = x + y \end{equation} [/latex] |
![]()
複数行の数式
eqnarray環境では、複数式を一つにまとめて扱える。
|
1 2 3 4 5 6 7 8 |
[latex] \begin{eqnarray} (a + b)^2 &=& a(a + b) + b(a + b) \\ &=& a^2 + b^2 + 2ab \\ (a + b)(a - b) &=& a(a - b) + b(a - b) \\ &=& a^2 - b^2 \end{eqnarray} [/latex] |
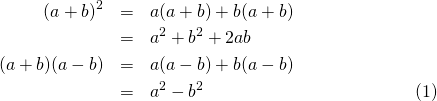
- 改行位置に”\\”を記述
- 等号などで縦位置を揃えたいときは、’&’で囲む
方程式の左を中括弧で囲いたい場合、\left\{とするが、eqnarray環境ではうまくいかない。array環境を使えばよいが、若干の注意点がある。
- 全体をequation環境で囲う(行番号が不要の場合にはequation*)
- 中括弧の場合は\{とエスケープする
- 右側の括弧を省略する場合は\right.
|
1 2 3 4 5 6 7 8 9 |
[latex] \begin{equation} \left\{ \begin{array}{lll} x + y & = & c \\ x ^2 + y^2 & = & r^2 \right. \end{array} \end{equation} [/latex] |
![]()
単に中央ぞろえで複数行の式を書きたい場合はgather環境が手軽。式番号は自動でつけてくれる(以下の例ではgather*として式番号を抑止している)。
|
1 2 3 4 5 6 7 8 |
[latex] \begin{gather} a x^2 + bx + c = 0 \\ a \left( x + \frac{b}{2a} \right) ^2 - \frac{b^2}{4a} + c = 0\\ x + \frac{b}{2a} = \pm \sqrt{\frac{1}{a} \frac{b^2 - 4ac}{4a}} \\ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{gather} [/latex] |
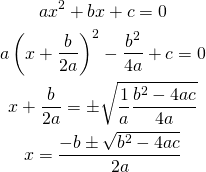
式中の任意の位置でそろえるにはalign環境と&記号を使う。たとえば全体をセンタリングしながらその中で式を左揃えにしたい場合、全ての式の先頭に&記号を置けばけばよい(もちろん、式ごとの揃える位置を変えることもできる)。
|
1 2 3 4 5 6 7 |
[latex] \begin{align} & x^2 + y^2 = r^2 \\ & x = r \cos \theta , y = r \sin \theta \\ & r^2 \cos ^2 \theta + r^2 \sin ^2 \theta = r^2 \end{align} [/latex] |
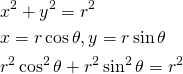
スペース
1文字、2文字分のスペース(quad, qquad)
\quad |
|
\qquad |
任意長のスペース(hspace)
| \hspace{12pt} | |
| \hspace{1pc} | |
| \hspace{12mm} | |
| \hspace{1.2cm} |
短いスペース
| \! | |
| \, | |
| \: | |
| \; |
\!は負のスペースで、後ろの文字を前へ詰める。
![]() (AとBの間に\!が4つ)
(AとBの間に\!が4つ)
任意の文字分のスペース
| \phantom{} |
分数・括弧
|
1 |
\left| \frac{c+d}{a+b} \right| ^2 = \left( \frac{c+d}{a+d} \right) ^2 = \left\{ \frac{c+d}{a+d} \right\} ^2 |
![]()
平方根・n乗根
|
1 2 |
l = \sqrt{x^2 + y^2} \\ \sqrt[n]{x} |
![]()
\sqrtのn乗根のnは”[n]”と大括弧で、数値xは”{x}”と中括弧で書いている点に注意。
指数表現・添字表現
|
1 |
z^n = x^n + y^n |
![]()
関数
三角関数
|
1 2 3 |
\sin x , \cos x , \tan x \sec x , \csc x , \cot x \arcsin x , \arccos x , \arctan x |
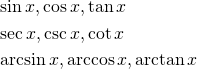
対数
|
1 |
\log_2 x , \log x , \ln x |
![]()
総和・総積
|
1 2 |
S = \sum_{n=1}^{10} n P = \prod_{m=1}^{10} m |
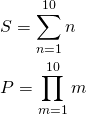
順列・組み合わせ
順列・組み合わせのように、記号の前にプレフィックスが付く場合は、ダミーに対してサフィックスを付ける。
|
1 2 3 |
[latex] {}_n P_k , \quad {}_n C_k [/latex] |
![]()
組み合わせを二項係数の形で書く場合は\binomを使う。使い方は\fracと同じで、分数などの中で小さくなるのを避ける場合には\dbinomを使う。
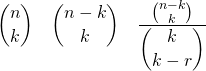
ベクトル・行列
ベクトル
列ベクトルはarray環境でn行1列とする。{c}は各要素を中央ぞろえで、左揃えならl、右揃えならr。
|
1 2 |
\vec{a} = (a_1, \cdots , a_n) {\bf a} = \left( \begin{array}{c} a_1\\ \vdots\\ a_n \end{array} \right) |
![]()
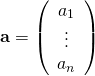
行列
行列はarray環境で
|
1 2 3 4 5 6 7 |
{\bf A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right] |
![Rendered by QuickLaTeX.com $$ {\bf A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right]$$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-385c4a4524601efa3098b5721d3d60a9_l3.png)
ベクトル・行列の太字表記
QuickLatexでベクトル・行列を太字で表記する方法。
|
1 |
\boldsymbol{Ax} = \lambda \boldsymbol{x} |
![]()
ノルム・垂直・平行
|
1 2 3 4 5 |
[latex] \| \boldsymbol{a} \| \\ \boldsymbol{a} \perp \boldsymbol{b} \\ \boldsymbol{a} \parallel \boldsymbol{b} [/latex] |
![]()
行列の転置
二通りの転置行列の記述方法。
|
1 2 |
{}^t \boldsymbol{A} \\ \boldsymbol{A} ^{\rm T} |
![]()
微分・積分
|
1 |
\frac{dy}{dx} = f'(x) |
![]()
|
1 |
\Delta = \nabla^2 = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} |
![]()
|
1 |
\int_a^b f(x) dx |
![]()
上括弧・下括弧
|
1 |
\overbrace{1, 2, 3, 4,}^{\rm over} \underbr = ace{5, 6, 7, 8}_{\rm under} |
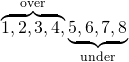
筆算
簡単な筆算は、arrayブロックで\hlineを使う。
|
1 2 3 4 5 6 |
\begin{array}{rr} & 12345 \\ + & 678 \\ \hline & 13023 \end{array} |
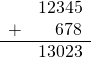
多項式の和になるとちょっとややこしい。
|
1 2 3 4 5 6 |
\begin{array}{rcccccc} A_n &= &a_1 &+ &\cdots &+ &a_n \\ B_n &= &b_1 &+ &\cdots &+ &b_n \\ \hline A_n + B_n &= &(a_1 + b_1) &+ &\cdots &+ &(a_n + b_n) \end{array} |