定義
(1) ![]()
性質
単独の行列
転置の転置
(2) ![]()
逆行列
(3) ![]()
[証明]
(4) 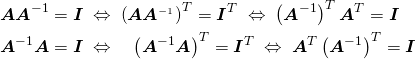
行列式
(5) ![]()
行列演算
線形性
(6) ![]()
(7) ![]()
積
交換法則は成り立たない。
(8) ![]()
[証明]
(9) ![Rendered by QuickLaTeX.com \begin{align*} \left( [ \boldsymbol{AB} ]_{ij} \right)^T = \left( \sum_k \boldsymbol{A}_{ik} \boldsymbol{B}_{kj} \right)^T = \sum_k \boldsymbol{B}_{jk} \boldsymbol{A}_{ki} =\boldsymbol{B}^T \boldsymbol{A}^T \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e0a675c84ad11bc2c66bd764f6b3dfeb_l3.png)
行列とベクトル
行列とベクトルの積
(10) ![]()
すなわち
(11) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{m1} \\ \vdots & & \vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-47268abd1fb09618f4ac57dcd0edb815_l3.png)
内積
(12) ![]()
すなわち
(13) ![Rendered by QuickLaTeX.com \begin{equation*} [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = x_1^2 + \cdots + x_n^2 \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d7eb4031678ac7ca0faa0eefd7cb4318_l3.png)
(1) ![]()
(2) ![]()
(3) ![]()
[証明]
(4) 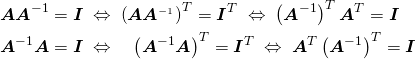
(5) ![]()
(6) ![]()
(7) ![]()
交換法則は成り立たない。
(8) ![]()
[証明]
(9) ![Rendered by QuickLaTeX.com \begin{align*} \left( [ \boldsymbol{AB} ]_{ij} \right)^T = \left( \sum_k \boldsymbol{A}_{ik} \boldsymbol{B}_{kj} \right)^T = \sum_k \boldsymbol{B}_{jk} \boldsymbol{A}_{ki} =\boldsymbol{B}^T \boldsymbol{A}^T \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e0a675c84ad11bc2c66bd764f6b3dfeb_l3.png)
(10) ![]()
すなわち
(11) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{m1} \\ \vdots & & \vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-47268abd1fb09618f4ac57dcd0edb815_l3.png)
(12) ![]()
すなわち
(13) ![Rendered by QuickLaTeX.com \begin{equation*} [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = x_1^2 + \cdots + x_n^2 \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d7eb4031678ac7ca0faa0eefd7cb4318_l3.png)