2の補数 – TauStation

1 簡単なケース
2 典型的なビット数の整数範囲

簡単なケース

正の数の表現

桁数が固定された2進数の加算を考える。たとえば4桁(4 bits)の場合に1ずつ加える。

$\begin{array}{cc} 0000 + 0001 = 0001 & (1)\\ 0001 + 0001 = 0010 & (2)\\ 0010 + 0001 = 0011 & (3)\\ 0011 + 0001 = 0100 & (4)\\ 0100 + 0001 = 0101 & (5)\\ 0101 + 0001 = 0110 & (6)\\ 0110 + 0001 = 0111 & (7) \end{array}$

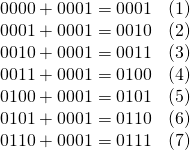
負の数の表現

一方、-1は0から1を引いた値として計算される。最初の計算だけ、上位桁から1を借りてこられるとして、以下の様な計算になる。

$\begin{array}{cc} 0000 - 0001 = 1111 & (-1)\\ 1111 - 0001 = 1110 & (-2)\\ 1110 - 0001 = 1101 & (-3)\\ 1101 - 0001 = 1100 & (-4)\\ 1100 - 0001 = 1011 & (-5)\\ 1011 - 0001 = 1010 & (-6)\\ 1010 - 0001 = 1001 & (-7)\\ 1001 - 0001 = 1000 & (-8) \end{array}$

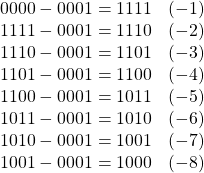
上の足し算の結果と下の引き算の結果をを見ると、以下のことがわかる。

正の数(0～7)と負の数(-8～-1)の合計15個で、4ビットの全てのパターンが網羅されている
正の数の最上位ビットは0、負の数の最上位ビットは1

引き算と補数の足し算

たとえば上の例で、正の数と負の数を加えてみる。

$\begin{array}{cl} 0101 + 1110 = 0011 & (5-2=3) \\ 0011 + 1001 = 1100 & (3-7=-4) \\ 1111 + 1100 = 1011 & (-1-4=-5) \end{array}$

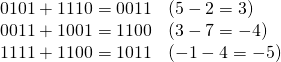
2の補数を計算したときに0からその数を減じているので、当然の結果ではある。いずれにしても、負数を2の補数で表現することで、減算を加算で代えることができる。

2の補数を得る方法

2の補数を得るのに、いちいち0から引かなくても、以下の方法で可能。

整数のビットパターンを反転
1を加える

4ビットの例では以下のとおり。

$\begin{array}{cc} 0001 \rightarrow 1110 \rightarrow 1111 & (-1)\\ 0010 \rightarrow1101 \rightarrow 1110 & (-2)\\ 0011 \rightarrow1100 \rightarrow 1101 & (-3)\\ 0100 \rightarrow1011 \rightarrow 1100 & (-4)\\ 0101 \rightarrow1010 \rightarrow 1011 & (-5)\\ 0110 \rightarrow1001 \rightarrow 1010 & (-6)\\ 0111 \rightarrow1000 \rightarrow 1001 & (-7)\\ 1000 \rightarrow0111 \rightarrow 1000 & (-8)\\ \end{array}$

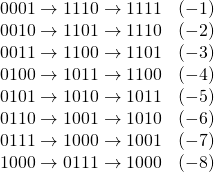
すなわち、固定長の整数の場合、ビット反転と加算機能があれば、減算を実現できる。

典型的なビット数の整数範囲

8ビット

byte型でよく見る値。

$\begin{array}{lllr} 0111\:1111 = &2^7 - 1 &=& 127 \\ 1000\:0000 = &-2^7 &=& -128 \end{array}$

16ビット

short型でよく見る値。

$\begin{array}{lllr} 0111\:1111\:1111\:1111 = &2^{15} - 1 &= &32767 \\ 1000\:0000\:0000\:0000 = &-2^{15} &= &-32768 \end{array}$

32ビット

一般的なint型で絶対値が約21億。

$\begin{array}{llr} 2^{31} - 1 &=& ‭2,147,483,647 \\ -2^{31} &=& -‭2,147,483,648‬ \end{array}$

64ビット

long型、絶対値が約920京（！）

$\begin{array}{llr} 2^{63} - 1 &=& ‭9,223,372,036,854,775,807 \\ -2^{63} &=& -‭9,223,372,036,854,775,808‬ \end{array}$