概要
三角形の2辺a、bとそのなす角θが与えられたとき、3つ目の辺cの長さは以下で求められる。
鋭角の場合
下図のように、辺a、bとそのなす角θが与えられているとき、3つ目の辺cとそれらとの関係を考える。
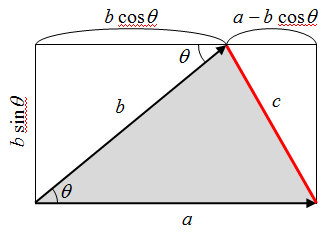
辺cは上図右の直角三角形の斜辺なので、以下の式が成り立つ。
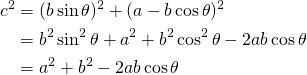
鈍角の場合
下図のようになす角が鈍角の場合を考える。
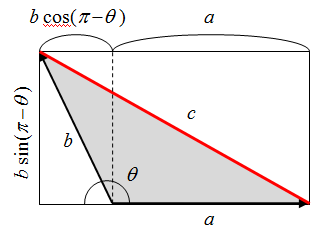
![$$ \begin{align*} c^2 &= \left[ b \sin ( \pi - \theta ) \right]^2 + \left[ b \cos ( \pi - \theta ) + a \right]^2 \\ &= (b \sin \theta )^2 + (-b \cos \theta + a)^2 \\ &= b^2 \sin ^2 \theta + b^2 \cos ^2 \theta + a^2 - 2ab \cos \theta \\ &= a^2 + b^2 - 2ab \cos \theta \end{align} $$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bbbc758041289d3592c77d7729f346bf_l3.png "Rendered by QuickLaTeX.com")
三角形の2辺a、bとそのなす角θが与えられたとき、3つ目の辺cの長さは以下で求められる。
下図のように、辺a、bとそのなす角θが与えられているとき、3つ目の辺cとそれらとの関係を考える。
辺cは上図右の直角三角形の斜辺なので、以下の式が成り立つ。
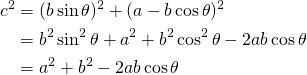
下図のようになす角が鈍角の場合を考える。