ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。
![]()
2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の![]() の長さを考える。
の長さを考える。
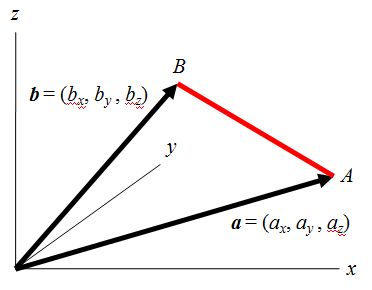
まずベクトルの成分で計算した場合は、
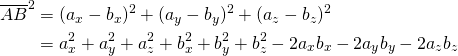
また余弦定理を用いて計算した場合は、![]() として以下のようになる。
として以下のようになる。
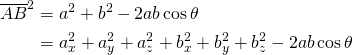
上記2つが等しいことから、以下が得られる。
![]()
2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。
ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。
![]()
2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の![]() の長さを考える。
の長さを考える。

まずベクトルの成分で計算した場合は、
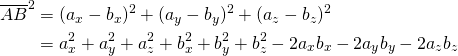
また余弦定理を用いて計算した場合は、![]() として以下のようになる。
として以下のようになる。
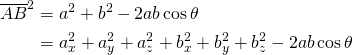
上記2つが等しいことから、以下が得られる。
![]()
2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。