概要
三角形の2辺a、bとそのなす角θが与えられたとき、3つ目の辺cの長さは以下で求められる。
![]()
鋭角の場合
下図のように、辺a、bとそのなす角θが与えられているとき、3つ目の辺cとそれらとの関係を考える。
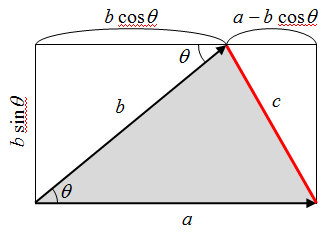
辺cは上図右の直角三角形の斜辺なので、以下の式が成り立つ。
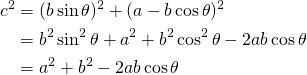
鈍角の場合
下図のようになす角が鈍角の場合を考える。
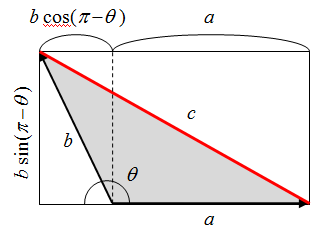
![Rendered by QuickLaTeX.com $$ \begin{align*} c^2 &= \left[ b \sin ( \pi - \theta ) \right]^2 + \left[ b \cos ( \pi - \theta ) + a \right]^2 \\ &= (b \sin \theta )^2 + (-b \cos \theta + a)^2 \\ &= b^2 \sin ^2 \theta + b^2 \cos ^2 \theta + a^2 - 2ab \cos \theta \\ &= a^2 + b^2 - 2ab \cos \theta \end{align} $$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bbbc758041289d3592c77d7729f346bf_l3.png)
三角形の2辺a、bとそのなす角θが与えられたとき、3つ目の辺cの長さは以下で求められる。
![]()
下図のように、辺a、bとそのなす角θが与えられているとき、3つ目の辺cとそれらとの関係を考える。

辺cは上図右の直角三角形の斜辺なので、以下の式が成り立つ。
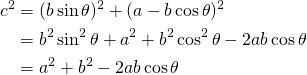
下図のようになす角が鈍角の場合を考える。

![Rendered by QuickLaTeX.com $$ \begin{align*} c^2 &= \left[ b \sin ( \pi - \theta ) \right]^2 + \left[ b \cos ( \pi - \theta ) + a \right]^2 \\ &= (b \sin \theta )^2 + (-b \cos \theta + a)^2 \\ &= b^2 \sin ^2 \theta + b^2 \cos ^2 \theta + a^2 - 2ab \cos \theta \\ &= a^2 + b^2 - 2ab \cos \theta \end{align} $$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bbbc758041289d3592c77d7729f346bf_l3.png)
ある点が運動しているとき、着目する他の点が進行方向の前方にあるのか、後方にあるのかを判定したい時があるが、2次元の場合は、ベクトルの内積を使うとこの判定が簡単にできる。
以下の図で、点sがvの方向に進んでいるとき、点pが前方/後方のいずれにあるかを判定する。
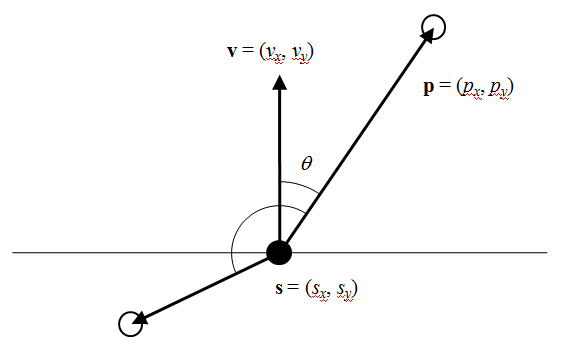
sを起点としたベクトルvと、sから見たpの相対的な位置ベクトルの内積を考えると、
![]()
上式で0≤θ≤90度の範囲であればpはsの前方にあり、このときcosθ≥0。また90度<θ≤180度の範囲ならpはsの後方にあり、cosθ<0となる。
内積を計算する角は、ベクトルvとpのなす角なので、pがsの左右どちらにあるかは問わない。
以上のことから、進行方向のベクトルvと、自身から見た相対的な着目点の位置ベクトルの内積が正なら着目点は前方に、負なら後方にあることになる(ゼロならば真横)。
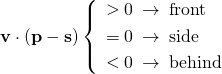
方向ベクトルvを90度回転させた上で上記の前後判定を行うことで左右判定が可能になる。
右へ回転させたベクトルに対して前方なら元の方向ベクトルの右、後方なら元の方向ベクトルの左と判定できる。
2次元の場合、2つのベクトルが平行かどうかを確かめるには、いずれか一方を90度回転させて、それが他のベクトルと直角であるかどうかを確かめるとよい(→ベクトルを90度回転させる方法)。
以下の2つのベクトルが平行かどうかを確認するには、
![]()
たとえば![]() を90度回転させて内積がゼロかどうかを確認する。
を90度回転させて内積がゼロかどうかを確認する。
![]()
なお、この式は、2つのベクトルの外積のx-y平面に垂直な成分(z成分)を計算していることになる。
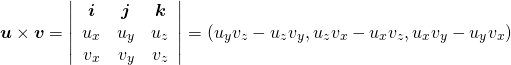
この2次元の2つのベクトルの場合、外積の絶対値はz成分の大きさにほかならず、その値は![]() に対応することから、この値がゼロの場合は
に対応することから、この値がゼロの場合は![]() すなわち平行を意味する。
すなわち平行を意味する。
なお数値計算上は、内積値の絶対値がある小さな値より小さいかどうかを判定することになる。
2つのベクトルが平行な時、そのなす角がゼロとなることから以下が成り立つ。
(1) ![]()
この等式についても、小さな値との比較で判定する。
下図のように互いに直交する2つのベクトルを考える。
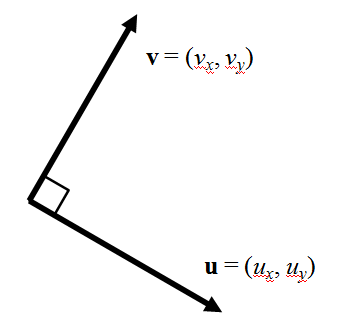
これらのベクトルが直角であるためには、内積がゼロとなればよい。
![]()
成分表示すれば
![]()
これを満足する最もわかりやすいベクトル![]() は、
は、![]() の要素を入れ替えて、何れか片方をマイナスとしたもの。
の要素を入れ替えて、何れか片方をマイナスとしたもの。
![]()
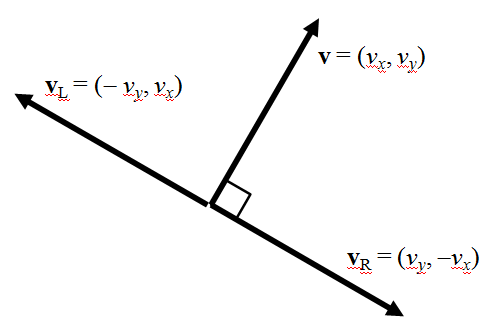
ここで要素を入れ替えた後のy成分をマイナスとしたベクトルは、元のベクトルを90度右に回転させたもので、x成分をマイナスとしたベクトルは、元のベクトルを90度左に回転させたもの。
これは回転行列を使って確かめることもできる。ただし以下の式で、+は左回り、-は右回りの回転であることに注意。
![]()