Poisson分布の標準形
ポアソン過程の到着数に現れる、離散確率分布。
(1) ![]()
全事象の確率が1となることの確認
(2) 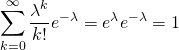
平均
(3) 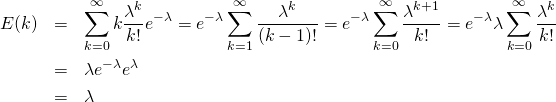
この過程で以下のようになっていることに留意。
(4) 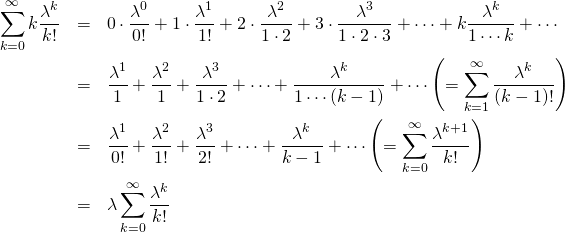
分散
(5) 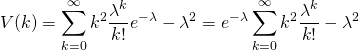
第一項の和の部分については、
(6) 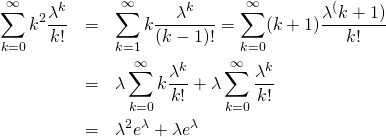
したがって分散は以下のように得られる。
(7) ![]()
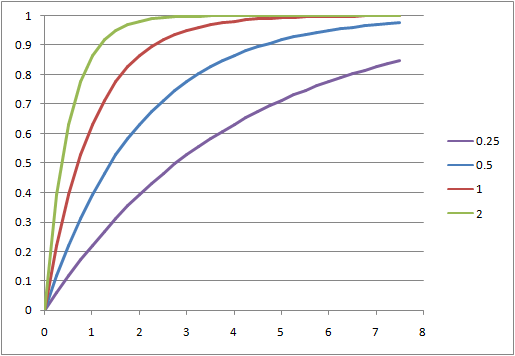
確率分布の形状と考察
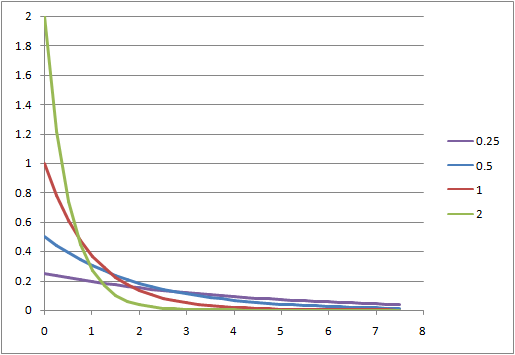
Poisson分布の形状の特徴は以下の通り。
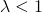 のときは単調減少
のときは単調減少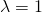 のとき
のとき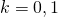 に対する確率が等しく、約0.368
に対する確率が等しく、約0.368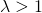 でピークが現れる。
でピークが現れる。
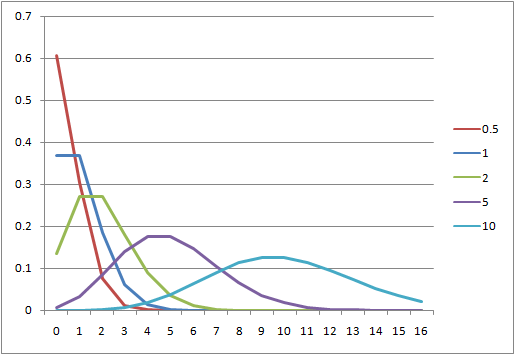
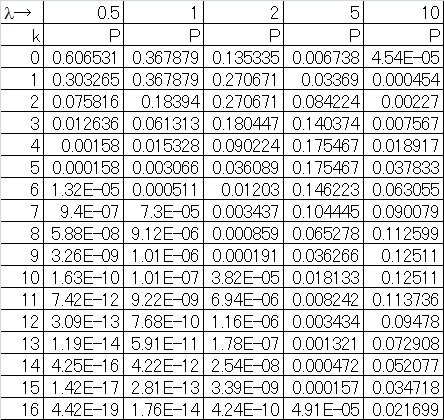
![]() は、その観測期間内に平均して1回も来ないようなケース。たとえば
は、その観測期間内に平均して1回も来ないようなケース。たとえば![]() だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか?といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。
だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか?といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。
![]() は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。
は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。
![]() の場合、
の場合、![]() の値に近いところで確率が最大となり、
の値に近いところで確率が最大となり、![]() の値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。
の値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} E(t) &=& \int_0^\infty t \lambda e^{- \lambda t} dt = \int_0^\infty x e^{-x} d \frac{x}{\lambda} \\ &=& \frac{1}{\lambda} \left( \int_0^\infty e^{-x} dx - \left[ x e^{-x} \right]_0^\infty \right) = \frac{1}{\lambda} \left[ - e^{-x} - x e^{-x} \right]_0^\infty \\ &=& \frac{1}{\lambda} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-4307189de1e2d97b96b989179d8376e9_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} V(t) &=& \int_0^\infty t^2 \lambda e^{-\lambda t} dt - \left( \frac{1}{\lambda} \right)^2 = \frac{1}{\lambda^2} \int_0^\infty x^2 e^{-x} dx - \frac{1}{\lambda^2} \\ &=& \frac{1}{\lambda^2} \left( 2 \int_0^\infty x e^{-x} dx - \left[ x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \left( \left[ -2 e^{-x} -2x e^{-x} - x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-3a2963bdd0340194dcbe135f02e853e2_l3.png)