Poisson分布の標準形
ポアソン過程の到着数に現れる、離散確率分布。
(1) ![]()
全事象の確率が1となることの確認
(2) 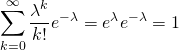
平均
(3) 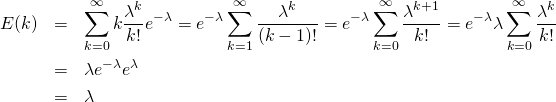
この過程で以下のようになっていることに留意。
(4) 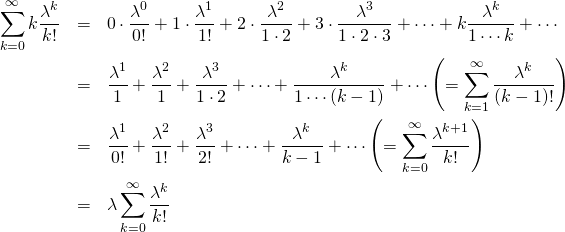
分散
(5) 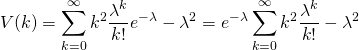
第一項の和の部分については、
(6) 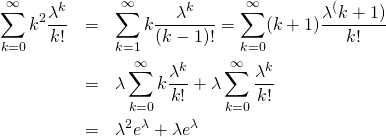
したがって分散は以下のように得られる。
(7) ![]()
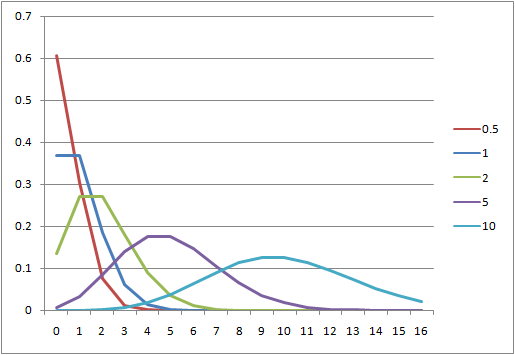
確率分布の形状と考察
Poisson分布の形状の特徴は以下の通り。
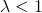 のときは単調減少
のときは単調減少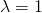 のとき
のとき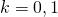 に対する確率が等しく、約0.368
に対する確率が等しく、約0.368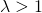 でピークが現れる。
でピークが現れる。
![]() は、その観測期間内に平均して1回も来ないようなケース。たとえば
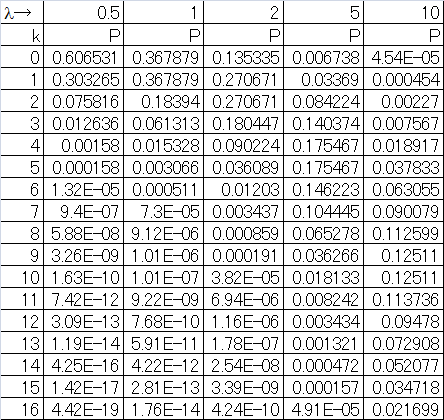
は、その観測期間内に平均して1回も来ないようなケース。たとえば![]() だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか?といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。
だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか?といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。
![]() は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。
は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。
![]() の場合、
の場合、![]() の値に近いところで確率が最大となり、
の値に近いところで確率が最大となり、![]() の値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。
の値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。