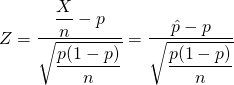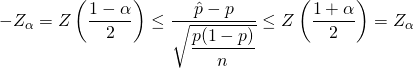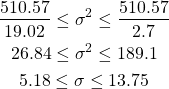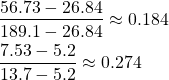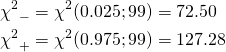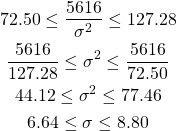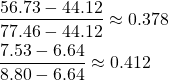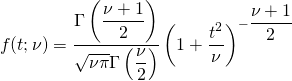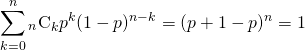PCR検査と条件付確率

2020-09-17 / tau / コメントする

概要

2020年9月時点で、COVID-19いわゆる新型コロナウイルス感染症は収束を見ていない。このコロナウイルスについて、PCR検査を増やすべきだ、いや効果はない／医療現場の負担が増えるだけ、といろいろな論が飛び交っている。

不思議なことに、多くの人の目に触れるマスメディアや一般的なネットのソースでは、殆どの場合定性的な、あるいはそれ以前の論拠もないようなものばかりが並んでいる。意図してネットで検索すると確率論を適用しているものも見られるが、残念ながらほとんどの人はこれらのコンテンツはその意義や存在さえ意識しないだろう。

新型コロナウイルスの場合、計算に必要なデータは未詳のようだが、少なくともベイズ理論を適用する教科書的なパターンの問題である。そこで、この機に学んだいくつかの用語や概念、計算過程などをまとめておく。

なお、難病検査を例にした条件付確率の考え方はこちらにまとめている。

基本のデータ

定義

鍵となる指標の定義を確認するとともに、その記号を以下のように定義する。

医学・疫学上の指標

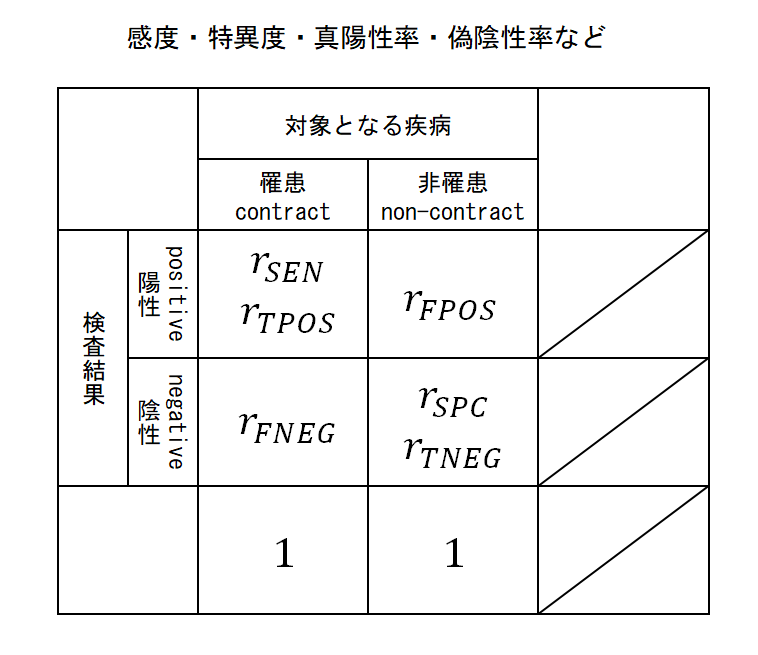
陽性率／陰性率

以下は罹患している／罹患していないことがわかっている人の集合に対する割合。

感度(sensitivity)：r_SEN
真陽性率(true positive rate)：r_TPOS: 罹患している人の検査結果が陽性と判定される割合。
特異度(specificity)：r_SPC
真陰性率(true negative rate)：r_TNEG: 罹患していない人の検査結果が陰性と判定される割合。
偽陽性率(false positive rate)：r_FPOS: 罹患していない人の検査結果が陽性と判定される割合。
偽陰性率(false negative rate)：r_FNEG: 罹患している人の検査結果が陰性と判定される割合。

これらの関係を図にすると以下の通り。真／偽の陽性率／陰性率は罹患者数のみあるいは非罹患者数のみの集団に対して、検査の判定結果を集計して計算される。表から、検査判定の陽性／陰性の割合は問題にしていないことがわかる。

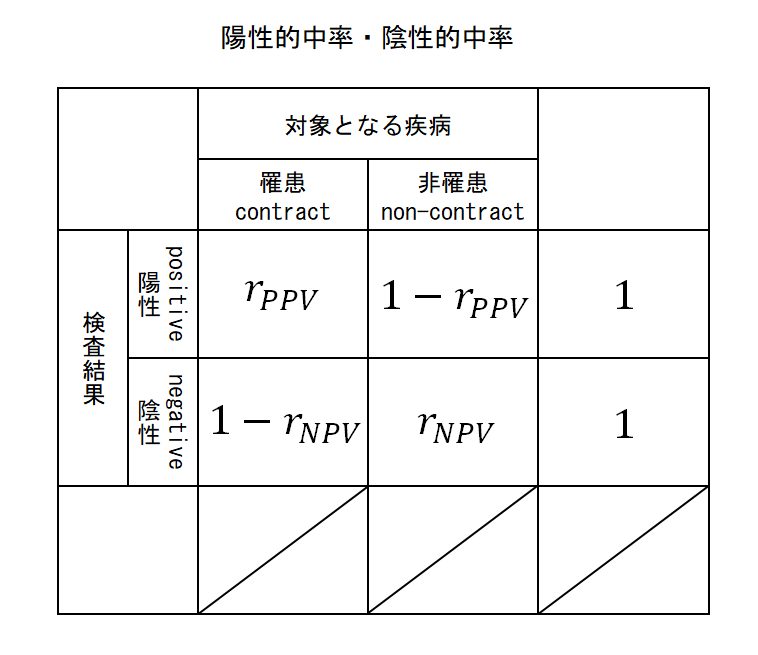
的中率

次に検査結果が判明している集団の実際の罹患状態に関する割合。

陽性的中率(Positive Predictive Value: PPV, PV+)：r_P_PV: 検査で陽性と判定された人のうち、実際に罹患者である割合。
陰性的中率(Negative Predictive Value: NPV, PV-)：r_NPV: 検査で非陽性と判定された人のうち、実際に罹患していない者である割合。

これらは検査の判定結果が陽性あるいは陰性の集団における罹患／非罹患の人の割合で、罹患している（あるいはしていない）人の全体の割合は問題にしていない。

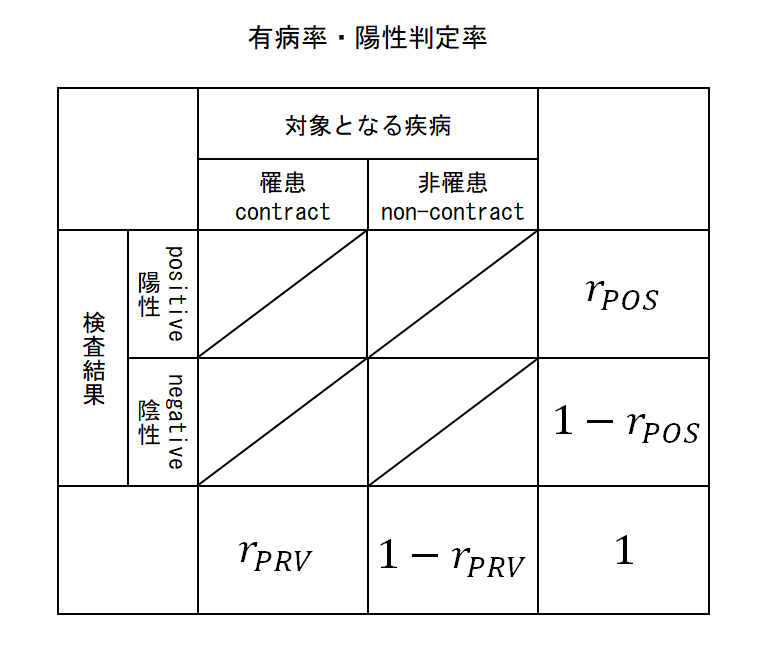
有病率／陽性率など

以下は対象となる集団全体における検査結果の割合や罹患状態の割合。

陽性率(positive rate)：r_pos: 検査で陽性と判定された人の割合。

有病率(Prevalence / Prevalence rate)：r_PRV: ある時点における疾病者数の人口に対する割合。
罹患率(Incidence / Incidence rate)：r_INC: ある期間において、疾病リスクのある人が対象とする疾病に罹患する割合。

これらは対象エリアの全員に対して罹患している人の割合、検査結果が陽性の人の割合である。有病率と罹患率の違いは一般にはあまり伝えられていないようだ。図にすると以下のようになる。

補足：感度と特異度について

「感度(sensitivity)」が「罹患している」という帰無仮説が真なのに検査で陰性と判定してしまう誤り、いわば「第一種の過誤」を起こさない確率と言える。

また「特異度(specificity)」が「罹患していない」という仮説（上の帰無仮説の対立仮説）が真なのに検査で陽性と判定してしまう誤り、すなわち「第二種の過誤」を起こさない確率と言える。

補足：「特異度」という表現について

「特異度」の用語には違和感がある。日本語の「特異な」ならsinglularやpeculiarの方が近く、specificは「明確な」、「特定の」というのが相当する（specifyという動詞もその意味でつかわれる）。「特別な」というニュアンスもあるようだが、「特異」というのは言い過ぎではないか。

specificityは罹患していない人を検査で陰性と正しく判定する割合なので、罹患していない人が大勢だとすると、その明白な事実を支持する割合、「明白度」とすると、ちょっと意味が分からなくなる。あるいは、その人が罹患していないということを特定するなら、せめて「特定度」くらいか。

いずれにしても、「特異度」という表現が使われているのは、英語の単語のニュアンスからしても、そもそもの意味合いからしても気持ちが悪い。

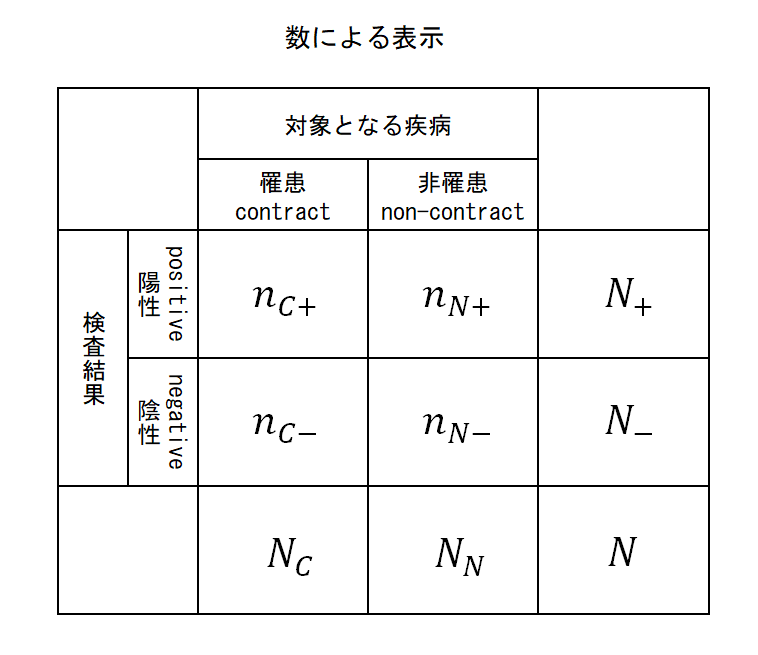
ここで定義する記号

C / N: 罹患している(contract)／罹患していない(non-contract)の人の集合
+ / −: 検査結果が陽性／陰性の人の集合
N: 検査人口
N₊ / N₋: それぞれ検査結果が陽性／陰性の人口
N_C / N_N: 検査を受けた人のうち、それぞれ罹患している(contract)／罹患していない(non-contract)人の人口
n_C₊ / n_C_– , n_N₊ / n_N_–: 検査を受けた人のうち、それぞれ、罹患していてかつ検査結果が陽性(C+)あるいは陰性(C−)、罹患しておらずかつ検査結果が陽性(N+)あるいは陰性(N−)の人の人口

これらを表で整理すると以下の通り。

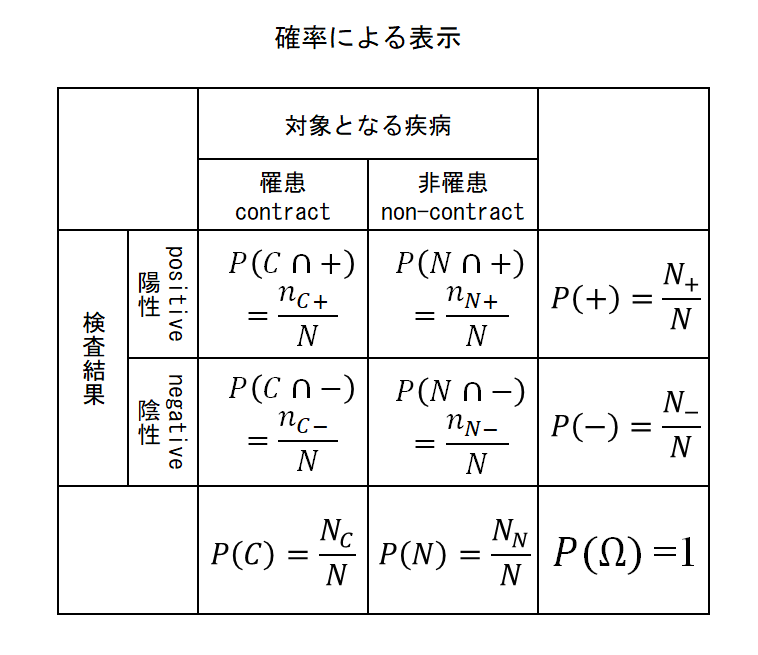
また、これらから計算される確率は以下の通り。

条件付確率による表示

感度／特異度（真陽性率／真陰性率）

感度や特異度は、ある人が罹患している／罹患していない場合に検査結果が陽性／陰性となる確率ともいえる。これを条件付確率で表示し、的中率による表現に変換すると以下のようになる。

(1) $\begin{align*} r_{SEN} = r_{TPOS} &= P(+|C) = \frac{P(C \cap +)}{P(C)} =\frac{P(C|+)P(+)}{P(C)} \\ &= \frac{r_{PPV} \cdot r_{POS}}{r_{PRV}}\\ r_{SPC} = r_{TNEG} &= P(-|N) = \frac{P(N \cap -)}{P(N)} = \frac{P(N|-)P(-)}{P(N)} \\ &= \frac{r_{NPV} \cdot (1 - r_{POS})}{1 - r_{PRV}} \end{align*}$

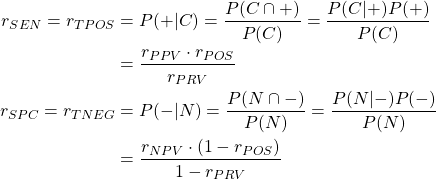
偽陽性率／偽陰性率

偽陽性／偽陰性についても条件付確率で表し、これらを的中率による表現に変換すると以下のようになる。

(2) $\begin{align*} r_{FPOS} &= P(+|N) = \frac{P(N \cap +)}{P(N)} = \frac{P(N|+) P(+)}{P(N)}\\ &= \frac{(1 - r_{PPV}) r_{POS}}{1 - r_{PRV}} \\ r_{FNEG} &= P(-|C) = \frac{P(C \cap -)}{P(C)} = \frac{P(C|-) P(-)}{P(C)} \\ &= \frac{(1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \end{align*}$

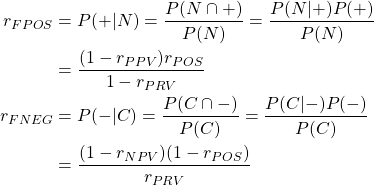
たとえばここで真陽性率と偽陰性率を加えると、

(3) $\begin{align*} r_{TPOS} + r_{FNEG} &= \frac{r_{PPV} \cdot r_{POS}}{r_{PRV}} + \frac{(1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \\ &= \frac{r_{PPV} \cdot r_{POS} + (1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \end{align*}$

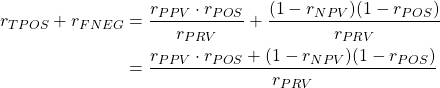
ここで総数Nを仮定して分母分子にかければ、結果は1となることがわかる。

陽性的中率／陰性的中率

的中率は検査の判定陽性／陰性に対して、その対象者が実際に罹患／非罹患である割合を表す。これを条件付確率で表して陽性率や陰性率で表すと以下のようになる。

(4) $\begin{align*} r_{PPV} &= P(C|+) = \frac{P(C \cap +)}{P(+)} =\frac{P(+|C)P(C)}{P(+)}\\ &= \frac{r_{SEN} \cdot r_{PRV}}{r_{POS}} \\ r_{NPV} &= P(N|-) = \frac{P(N \cap -)}{P(-)} = \frac{P(-|N)P(N)}{P(-)} \\ &= \frac{r_{SPC} \cdot (1 - r_{PRV})}{1 - r_{POS}} \end{align*}$

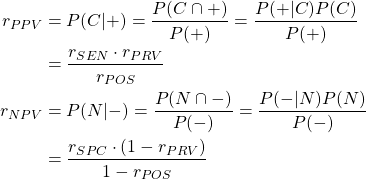
実際の使われ方

多くの場合、検査方法の精度を確認するには、「罹患している人と罹患していない人を連れてきて検査をしてみる」というのが妥当だろう。感染症などで疑いがある人が医療機関に集まるから、そういうところで臨床的に試すのだろう。場合によって臨床例が少ない場合は、とにかく検査方法を適用しながら、実際の罹患状態をトレースするという方法がとられるのかもしれないが。

ただCOVID-19のPCR検査の場合、データが公表されていないのかどうかわからないが、感度については適当に（あるいは他サイトで使われている値を持ってきて）設定したりしているものしか見当たらない。以下のような手順が見られる。

感度と特異度を適当に設定する。感度は70%、特異度は99%というのがほとんど。
対象エリアの陽性者数nと総人口Nを持ってくる。
陽性者数を感度で割って、罹患者数を算出。
罹患者数を総人口で割って有病率を算出。
総人口から有病人口を引いて非罹患者数を算出。
非罹患者数と特異度の定義から偽陽性者数を算出。
以上のパラメーターを使って陽性的中率を算出。

計算された陽性的中率がかなり低いと主張しているものや、オーソリティーがありそうなサイトでも例題みたいな数字を示して有病率10%くらいで設定したりしているものや、結構混乱しているようだ。

ここで陽性的中率を感度で微分して、感度を見てみる（ややこしい）。

(5) $\begin{align*} \frac{d r_{PPV}}{d r_{SEN}} = \frac{r_{PRV}}{r_{POS}} \\ \end{align*}$

有病率が10000人に一人、陽性判定率が100人にひとりくらいなら、1%くらいで、感度（真陽性率）が数十%くらい違っても差は出なさそうだ。それよりも有病率がかなり低いと、いくら高感度の検査方法でも陽性的中率がかなり低くなりそうなことが式から読み取れる。

一方偽陽性率の方は、有病率や陽性的中率が結構低いとすると、陽性判定率の値が効いてくる。これは結構無視できないレベルのように思えるが。

ただ、共通して使えるデータが見当たらないので、数値の信憑性が揺らいでいるように思える。罹患・非罹患を計算するのに母数にエリアの全人口を使ったりするのは、検査をしていない人すべてを非罹患とみているので有病率を過少に見積もることになるだろう。

退院前の検査を含むかどうかなど定義の問題はあるが、そのようなフラグを立てたデータを集約するだけでも有益な情報になると思う。

ブートストラップサンプリング

2020-06-20 / tau / コメントする

概要

母集団から得られたサンプルから標本をつくり、それに対して統計的な検討を加える方法。限られたサンプルデータから異なる再標本を大量に作り(resampling)、母集団パラメーターの推定、アンサンブル機械学習のデータなどに用いる。

以下は、1次元配列に対してnumpy.random.choice()で並べ替えた再標本を複数生成している例。

import numpy as np

np.random.seed(0)

a = np.arange(10)

for n in range(5):
    print(np.random.choice(a, len(a)))

# [5 0 3 3 7 9 3 5 2 4]
# [7 6 8 8 1 6 7 7 8 1]
# [5 9 8 9 4 3 0 3 5 0]
# [2 3 8 1 3 3 3 7 0 1]
# [9 9 0 4 7 3 2 7 2 0]

import numpy as np

np.random.seed(0)

a = np.arange(10)

for n in range(5):

print(np.random.choice(a, len(a)))

# [5 0 3 3 7 9 3 5 2 4]

# [7 6 8 8 1 6 7 7 8 1]

# [5 9 8 9 4 3 0 3 5 0]

# [2 3 8 1 3 3 3 7 0 1]

# [9 9 0 4 7 3 2 7 2 0]

ブートストラップ(bootstrap)とはブーツの後ろについているつまみ／輪っかのことで、ここを持ったりフックをかけてブーツを引っ張り上げる。19世紀にはブートストラップを引っ張って自分自身を引っ張り上げる、という不可能なことの比喩に使われていたが、20世紀に入って自分自身で何とかすることや自己完結の仕組みなどの比喩に使われるようになったとのこと。コンピューターの起動を指すブートもbootstrapを略。

ブートストラップ法による信頼区間の推定

再標本を大量に生成することで、パラメーターの信頼区間などの統計量を直接得ることができる。

e-statの身長・体重に関する国民健康・栄養調査2017年のデータから、40歳代の日本国民の身長の平均171.2cm及び標準偏差6.0cmを母集団のパラメーターとして用いる（データ数は374人）。

このパラメーターから、正規分布に従う10個の乱数を発生させる。

180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7

1	180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

np.random.seed(1)

pop_mean = 171.2
pop_std = 6
sample_size = 10
resample_size = sample_size
n_boots = 1000
conf_prob = np.array([0.025, 0.975])

sample = np.random.normal(pop_mean, pop_std, sample_size)
sample_mean = np.mean(sample)
sample_uvar = np.var(sample, ddof=1)
sample_std = np.sqrt(sample_uvar)

import numpy as np

import matplotlib.pyplot as plt

import scipy.stats as stats

np.random.seed(1)

pop_mean = 171.2

pop_std = 6

sample_size = 10

resample_size = sample_size

n_boots = 1000

conf_prob = np.array([0.025, 0.975])

sample = np.random.normal(pop_mean, pop_std, sample_size)

sample_mean = np.mean(sample)

sample_uvar = np.var(sample, ddof=1)

sample_std = np.sqrt(sample_uvar)

次に、サンプルデータセットからブートストラップサンプリングで再標本を多数発生させ、それらの平均を一つのデータセットとする。

resample_means = []
for i in range(n_boots):
    resample = np.random.choice(sample, resample_size)
    resample_means.append(np.mean(resample))

resample_means = []

for i in range(n_boots):

resample = np.random.choice(sample, resample_size)

resample_means.append(np.mean(resample))

numpy.percentile()で95 %信頼区間（2.5%～97.5%）を計算。

resample_conf = np.percentile(resample_means, conf_prob*100)

1	resample_conf = np.percentile(resample_means, conf_prob*100)

比較のため、元のサンプルについてt分布による平均の信頼区間も計算。scipy.stats.tのinterval()でも求められるが、ここでは愚直に元の計算式から計算した。

sample_conf = \
    sample_mean + \
    stats.t.ppf(conf_prob, df=sample_size-1) * \
        np.sqrt(sample_uvar / sample_size)

sample_conf = \

sample_mean + \

stats.t.ppf(conf_prob, df=sample_size-1) * \

np.sqrt(sample_uvar / sample_size)

これらの結果、元の10個のサンプルの分布と1000個の再標本の平均の分布は以下のとおりで、釣り鐘状のきれいな分布となっている。

この時の各種データは以下の通り。

再標本の分散(不偏分散)は2.186と母集団やサンプルの分散より小さいが、これは多数の再標本の平均値の分散であり、母集団や元のサンプルの分散とは意味が違う。

また、10個のデータからt分布で推定した信頼区間よりも、ブートストラップで得られた信頼区間の方が狭くなっている。この傾向は乱数系列によって変わらず、一般的な傾向のようである。

Mean and STD
population   : 171.2, 6.000
sample       : 170.6, 7.532
resample mean: 170.6, 2.186
Confidence interval
sample       : 165.23 - 176.01 (10.78)
resample mean: 166.34 - 174.96 ( 8.62)

Mean and STD

population : 171.2, 6.000

sample : 170.6, 7.532

resample mean: 170.6, 2.186

Confidence interval

sample : 165.23 - 176.01 (10.78)

resample mean: 166.34 - 174.96 ( 8.62)

以下は再標本数を1000から100にした場合だが、分布形状は整っていて信頼区間もt分布による推定より狭い。なお、再標本数を10万、100万と増やしても、これ以上分散は小さくならず、信頼区間も変化しない。

Mean and STD
population   : 171.2, 6.000
sample       : 170.6, 7.532
resample mean: 170.9, 2.220
Confidence interval
sample       : 165.23 - 176.01 (10.78)
resample mean: 166.21 - 175.32 ( 9.11)

Mean and STD

population : 171.2, 6.000

sample : 170.6, 7.532

resample mean: 170.9, 2.220

Confidence interval

sample : 165.23 - 176.01 (10.78)

resample mean: 166.21 - 175.32 ( 9.11)

異常の計算・表示のコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

np.random.seed(1)

pop_mean = 171.2
pop_std = 6
sample_size = 10
resample_size = sample_size
n_boots = 1000
conf_prob = np.array([0.025, 0.975])

sample = np.random.normal(pop_mean, pop_std, sample_size)
sample_mean = np.mean(sample)
sample_uvar = np.var(sample, ddof=1)
sample_std = np.sqrt(sample_uvar)

resample_means = []
for i in range(n_boots):
    resample = np.random.choice(sample, resample_size)
    resample_means.append(np.mean(resample))

resample_means_mean = np.mean(resample_means)
resample_means_std = np.sqrt(np.var(resample_means, ddof=1))
resample_conf = np.percentile(resample_means, conf_prob*100)

sample_conf = \
    sample_mean + \
    stats.t.ppf(conf_prob, df=sample_size-1) * \
        np.sqrt(sample_uvar / sample_size)

print ("Mean and STD")
print("population   : {:5.1f}, {:5.3f}".format(pop_mean, pop_std))
print("sample       : {:5.1f}, {:5.3f}".format(sample_mean, sample_std))
print("resample mean: {:5.1f}, {:5.3f}".
    format(resample_means_mean, resample_means_std))
print("Confidence interval")
print("sample       : {:6.2f} - {:6.2f} ({:5.2f})".
    format(sample_conf[0], sample_conf[1], sample_conf[1] - sample_conf[0]))
print("resample mean: {:6.2f} - {:6.2f} ({:5.2f})".
    format(resample_conf[0], resample_conf[1], resample_conf[1] - resample_conf[0]))

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))
axs[0].hist(sample, ec='k')
axs[1].hist(resample_means, bins=10, ec='k')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

import scipy.stats as stats

np.random.seed(1)

pop_mean = 171.2

pop_std = 6

sample_size = 10

resample_size = sample_size

n_boots = 1000

conf_prob = np.array([0.025, 0.975])

sample = np.random.normal(pop_mean, pop_std, sample_size)

sample_mean = np.mean(sample)

sample_uvar = np.var(sample, ddof=1)

sample_std = np.sqrt(sample_uvar)

resample_means = []

for i in range(n_boots):

resample = np.random.choice(sample, resample_size)

resample_means.append(np.mean(resample))

resample_means_mean = np.mean(resample_means)

resample_means_std = np.sqrt(np.var(resample_means, ddof=1))

resample_conf = np.percentile(resample_means, conf_prob*100)

sample_conf = \

sample_mean + \

stats.t.ppf(conf_prob, df=sample_size-1) * \

np.sqrt(sample_uvar / sample_size)

print ("Mean and STD")

print("population : {:5.1f}, {:5.3f}".format(pop_mean, pop_std))

print("sample : {:5.1f}, {:5.3f}".format(sample_mean, sample_std))

print("resample mean: {:5.1f}, {:5.3f}".

format(resample_means_mean, resample_means_std))

print("Confidence interval")

print("sample : {:6.2f} - {:6.2f} ({:5.2f})".

format(sample_conf[0], sample_conf[1], sample_conf[1] - sample_conf[0]))

print("resample mean: {:6.2f} - {:6.2f} ({:5.2f})".

format(resample_conf[0], resample_conf[1], resample_conf[1] - resample_conf[0]))

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

axs[0].hist(sample, ec='k')

axs[1].hist(resample_means, bins=10, ec='k')

plt.show()

母比率の信頼区間

2020-06-18 / tau / コメントする

Bernoulli試行の成功確率をpとする。この試行をn回繰り返す場合の二項分布に従う確率変数X（成功回数）の平均と分散は以下で表される。

(1) $\begin{align*} E(X) &= np \\ V(X) &= np(1 - p) \end{align*}$

試行回数nが大きいとき、中心極限定理より以下の確率変数は標準正規分布に従う。

(2) $\begin{equation*} Z = \frac{X - np}{\sqrt{np(1 - p)}} \end{equation*}$

分母・分子をnで割り、サンプルから観測された確率として $X/n = \hat{p}$ と置く。

(3) $\begin{equation*} Z = \frac{\dfrac{X}{n} - p}{\sqrt{\dfrac{p(1 - p)}{n}}} = \frac{\hat{p} - p}{\sqrt{\dfrac{p(1 - p)}{n}}} \end{equation*}$

Zが標準正規分布に従うことから、信頼確率αの信頼区間は以下のように表せる。

(4) $\begin{equation*} -Z_\alpha = Z\left( \frac{1 - \alpha}{2} \right) \le \frac{\hat{p} - p}{\sqrt{\dfrac{p(1 - p)}{n}}} \le Z\left( \frac{1 + \alpha}{2} \right) = Z_\alpha \end{equation*}$

これよりpの信頼区間は以下のように表せる。

(5) $\begin{equation*} \hat{p} - Z_\alpha \sqrt{\dfrac{p(1 - p)}{n}} \le p \le \hat{p} + Z_\alpha \sqrt{\dfrac{p(1 - p)}{n}} \end{equation*}$

ここで信頼区間の境界値の計算に母比率pが含まれているが、nが大きいときは $\hat{p} = p$ として、以下を得る。

(6) $\begin{equation*} \hat{p} - Z_\alpha \sqrt{\dfrac{\hat{p}(1 - \hat{p})}{n}} \le p \le \hat{p} + Z_\alpha \sqrt{\dfrac{\hat{p}(1 - \hat{p})}{n}} \end{equation*}$

ここで、母比率0～1.0のBernoulli試行を繰り返し数を変えて試行したときの観測確率について、その平均と標準偏差がどうなるか計算してみた。

import numpy as np
import scipy.stats as stats
import pandas as pd


def p_trials(n, p, m):
    sum_p = []
    for traial in range(m):
        x = stats.uniform.rvs(size=n)
        sum_p.append(len(x[x<p]) / n)
    return np.mean(sum_p), np.std(sum_p, ddof=1)


np.random.seed(0)

p_list = np.arange(0, 1.1, 0.1)
n_list = [10, 20, 30, 50, 100, 1000]
n_trials = 100

mean_results = np.empty((len(p_list), len(n_list)))
std_results = np.empty((len(p_list), len(n_list)))

for cp, p in enumerate(p_list):
    for cn, n in enumerate(n_list):
        mean, std = p_trials(n, p, n_trials)
        mean_results[cp, cn] = mean
        std_results[cp, cn] = std

pd.options.display.precision = 3

df_mean = pd.DataFrame(mean_results, columns=n_list)
df_mean["p"] = p_list
columns = ["p"] + n_list
df_mean = df_mean.loc[:, columns]

df_std = pd.DataFrame(std_results, columns=n_list)
df_std["p"] = p_list
columns = ["p"] + n_list
df_std = df_std.loc[:, columns]

print(df_mean)
print(df_std)

import numpy as np

import scipy.stats as stats

import pandas as pd

def p_trials(n, p, m):

sum_p = []

for traial in range(m):

x = stats.uniform.rvs(size=n)

sum_p.append(len(x[x<p]) / n)

return np.mean(sum_p), np.std(sum_p, ddof=1)

np.random.seed(0)

p_list = np.arange(0, 1.1, 0.1)

n_list = [10, 20, 30, 50, 100, 1000]

n_trials = 100

mean_results = np.empty((len(p_list), len(n_list)))

std_results = np.empty((len(p_list), len(n_list)))

for cp, p in enumerate(p_list):

for cn, n in enumerate(n_list):

mean, std = p_trials(n, p, n_trials)

mean_results[cp, cn] = mean

std_results[cp, cn] = std

pd.options.display.precision = 3

df_mean = pd.DataFrame(mean_results, columns=n_list)

df_mean["p"] = p_list

columns = ["p"] + n_list

df_mean = df_mean.loc[:, columns]

df_std = pd.DataFrame(std_results, columns=n_list)

df_std["p"] = p_list

columns = ["p"] + n_list

df_std = df_std.loc[:, columns]

print(df_mean)

print(df_std)

まずpの平均についてはn = 10でもそれなりの精度となっていて、あまり試行回数による変化は大きくない。

      p     10     20     30     50    100   1000
0   0.0  0.000  0.000  0.000  0.000  0.000  0.000
1   0.1  0.093  0.102  0.105  0.099  0.097  0.101
2   0.2  0.215  0.194  0.196  0.208  0.206  0.203
3   0.3  0.328  0.287  0.295  0.297  0.299  0.299
4   0.4  0.393  0.384  0.394  0.396  0.407  0.399
5   0.5  0.494  0.491  0.514  0.494  0.497  0.498
6   0.6  0.596  0.609  0.605  0.592  0.598  0.600
7   0.7  0.695  0.714  0.704  0.698  0.694  0.700
8   0.8  0.811  0.807  0.799  0.791  0.793  0.798
9   0.9  0.910  0.904  0.887  0.898  0.903  0.902
10  1.0  1.000  1.000  1.000  1.000  1.000  1.000

p 10 20 30 50 100 1000

0 0.0 0.000 0.000 0.000 0.000 0.000 0.000

1 0.1 0.093 0.102 0.105 0.099 0.097 0.101

2 0.2 0.215 0.194 0.196 0.208 0.206 0.203

3 0.3 0.328 0.287 0.295 0.297 0.299 0.299

4 0.4 0.393 0.384 0.394 0.396 0.407 0.399

5 0.5 0.494 0.491 0.514 0.494 0.497 0.498

6 0.6 0.596 0.609 0.605 0.592 0.598 0.600

7 0.7 0.695 0.714 0.704 0.698 0.694 0.700

8 0.8 0.811 0.807 0.799 0.791 0.793 0.798

9 0.9 0.910 0.904 0.887 0.898 0.903 0.902

10 1.0 1.000 1.000 1.000 1.000 1.000 1.000

次にpの標準偏差（不偏分散の平方根）を見てみる。母比率が1/2に近いほどばらつきは大きく、試行回数nが大きいほどばらつきは小さくなっている。実務的にはn = 50～100あたりでそれなりのばらつきで観測確率をを母比率の代わりに用いてよいだろうか。

      p     10     20     30     50    100   1000
0   0.0  0.000  0.000  0.000  0.000  0.000  0.000
1   0.1  0.090  0.067  0.061  0.041  0.029  0.010
2   0.2  0.120  0.092  0.083  0.053  0.038  0.011
3   0.3  0.162  0.103  0.090  0.068  0.043  0.013
4   0.4  0.145  0.110  0.079  0.074  0.049  0.016
5   0.5  0.148  0.105  0.094  0.060  0.048  0.016
6   0.6  0.150  0.124  0.102  0.069  0.047  0.016
7   0.7  0.127  0.106  0.084  0.060  0.042  0.015
8   0.8  0.117  0.098  0.065  0.052  0.036  0.012
9   0.9  0.089  0.060  0.056  0.043  0.030  0.010
10  1.0  0.000  0.000  0.000  0.000  0.000  0.000

p 10 20 30 50 100 1000

0 0.0 0.000 0.000 0.000 0.000 0.000 0.000

1 0.1 0.090 0.067 0.061 0.041 0.029 0.010

2 0.2 0.120 0.092 0.083 0.053 0.038 0.011

3 0.3 0.162 0.103 0.090 0.068 0.043 0.013

4 0.4 0.145 0.110 0.079 0.074 0.049 0.016

5 0.5 0.148 0.105 0.094 0.060 0.048 0.016

6 0.6 0.150 0.124 0.102 0.069 0.047 0.016

7 0.7 0.127 0.106 0.084 0.060 0.042 0.015

8 0.8 0.117 0.098 0.065 0.052 0.036 0.012

9 0.9 0.089 0.060 0.056 0.043 0.030 0.010

10 1.0 0.000 0.000 0.000 0.000 0.000 0.000

以下はB(n, 0.5)についてnを変化させたときの観測確率のグラフで、やはりn = 50あたりまでにばらつきが急に減っていることがわかる。

母分散・標準偏差の信頼区間～カイ二乗分布

2020-06-16 / tau / コメントする

概要

母集団が母分散σ²の正規分布に従うとき、そこから抽出されたサンプルのサンプルサイズをn、不偏分散をs²とすると、以下のχ²は自由度n−1のカイ二乗分布に従う。

(1) $\begin{equation*} \chi^2 = \frac{(n - 1) s^2}{\sigma^2} \end{equation*}$

このことを利用して、母分散の信頼区間を推定する。

手順

母集団から取り出したn個のサンプルから不偏分散s²を計算する。

(2) $\begin{equation*} s^2 = \frac{1}{n - 1} \sum_{i=1}^n (x_i - \overline{x} )^2 \end{equation*}$

意図する確率αを定め、自由度n−1に対するχ²値を求める。両側の境界を持つ信頼区間の場合、χ²分布は左右非対称なので、左側・右側についてχ²((1−α)/2; n−1)とを算出する。

(3) $\begin{align*} {\chi^2}_- &= \chi^2\left(\frac{1 - \alpha}{2}; n - 1 \right) \\ {\chi^2}_+ &= \chi^2\left(\frac{1 + \alpha}{2}; n - 1 \right) \end{align*}$

これらを用いて信頼区間を設定する。

(4) $\begin{equation*} {\chi^2}_- \le \frac{(n - 1) s^2}{\sigma^2} \le {\chi^2}_+ \end{equation*}$

これをについて以下のように変形して母分散の信頼区間を得る。

(5) $\begin{equation*} \frac{(n - 1) s^2}{{\chi^2}_+} \le \sigma^2 \le \frac{(n - 1) s^2}{{\chi^2}_-} \end{equation*}$

例題

このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。

180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7

1	180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7

これらのデータの不偏分散は56.73であり、これとサンプルサイズ10から以下のχ²統計量を準備する。

(6) $\begin{equation*} \chi^2 = \frac{(n - 1) s^2}{\sigma^2} = \frac{9 \times 56.73}{\sigma^2} = \frac{510.57}{\sigma^2} \end{equation*}$

一方、95%確率に対するカイ二乗分布の両側の値は以下のように得られる。

(7) $\begin{align*} {\chi^2}_- &= \chi^2(0.025; 9) = 2.7\\ {\chi^2}_+ &= \chi^2(0.975; 9) = 19.02 \end{align*}$

これらからχ²統計量の信頼区間を設定。

(8) $\begin{equation*} 2.7 \le \frac{510.57}{\sigma^2} \le 19.02 \end{equation*}$

移項してσ²及びσの信頼区間を得る。

(9) $\begin{gather*} \frac{510.57}{19.02} \le \sigma^2 \le \frac{510.57}{2.7} \\ 26.84 \le \sigma^2 \le 189.1 \\ 5.18 \le \sigma \le 13.75 \end{gather*}$

ところで、不偏分散s² = 56.73やその平方根s = 7.53は、信頼区間の中央ではなくかなり左に寄っていることがわかる。

(10) $\begin{align*} &\frac{56.73 - 26.84}{189.1 - 26.84} \approx 0.184 \\ &\frac{7.53 - 5.2}{13.7 - 5.2} \approx 0.274 \end{align*}$

これはカイ二乗分布の確率密度が左右非対称であることに由来している。もし同じ不偏分散が100個のデータから得られたものだとするとカイ二乗分布の確率密度関数は左右対称に近づき、推定値は信頼区間の中央に近くなることが予想される。まずn = 100に対するχ²値は以下のようになる。

(11) $\begin{equation*} \chi^2 = \frac{99 \times 56.73}{\sigma^2} \approx \frac{5616}{\sigma^2} \end{equation*}$

また、95%確率に対するカイ二乗分布の両側の値は以下のように得られる。

(12) $\begin{align*} {\chi^2}_- &= \chi^2(0.025; 99) = 72.50\\ {\chi^2}_+ &= \chi^2(0.975; 99) = 127.28 \end{align*}$

σ²およびσの信頼区間は以下のようになる。

(13) $\begin{gather*} 72.50 \le \frac{5616}{\sigma^2} \le 127.28 \\ \frac{5616}{127.28} \le \sigma^2 \le \frac{5616}{72.50} \\ 44.12 \le \sigma^2 \le 77.46 \\ 6.64 \le \sigma \le 8.80 \end{gather*}$

不偏分散s² = 56.73やその平方根s = 7.53の信頼区間の中での位置を見てみると、中央に近くなっていることがわかる。

(14) $\begin{align*} &\frac{56.73 - 44.12}{77.46 - 44.12} \approx 0.378 \\ &\frac{7.53 - 6.64}{8.80 - 6.64} \approx 0.412 \end{align*}$

サンプルサイズに対する信頼区間の傾向

サンプルサイズを大きくしていったときの標準偏差の信頼区間の傾向は以下の通り。母集団の標準偏差に対して上側区間の方が広く、下側区間の方が狭くなっている。サンプルサイズが大きくなるとこの差は小さくなるが、それでも若干のインバランスは残っている。

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

np.random.seed(0)

h_pop_mean = 171.2
h_pop_std = 6
h_pop_var = h_pop_std**2

sample_size_list = range(10, 200)
prob_lower = 0.025
prob_upper = 0.975

fig, ax = plt.subplots()

std_cil_list = []
std_cir_list = []
for n in sample_size_list:
    h_smp = stats.norm.rvs(loc=h_pop_mean, scale=h_pop_std, size=n)
    uvar = np.var(h_smp, ddof=1)
    chil = stats.chi2.ppf(prob_lower, df=n-1)
    chir = stats.chi2.ppf(prob_upper, df=n-1)
    std_cil_list.append(np.sqrt((n - 1) * uvar / chir))
    std_cir_list.append(np.sqrt((n - 1) * uvar / chil))

ax.plot(sample_size_list, std_cil_list)
ax.plot(sample_size_list, std_cir_list)
ax.plot(sample_size_list, [h_pop_std]*len(sample_size_list))

ax.set_xlabel("number of samples")
ax.set_ylabel("STD of height(cm)")
ax.set_title("Confidence Interval of STD")

plt.show()

import numpy as np

import scipy.stats as stats

import matplotlib.pyplot as plt

np.random.seed(0)

h_pop_mean = 171.2

h_pop_std = 6

h_pop_var = h_pop_std**2

sample_size_list = range(10, 200)

prob_lower = 0.025

prob_upper = 0.975

fig, ax = plt.subplots()

std_cil_list = []

std_cir_list = []

for n in sample_size_list:

h_smp = stats.norm.rvs(loc=h_pop_mean, scale=h_pop_std, size=n)

uvar = np.var(h_smp, ddof=1)

chil = stats.chi2.ppf(prob_lower, df=n-1)

chir = stats.chi2.ppf(prob_upper, df=n-1)

std_cil_list.append(np.sqrt((n - 1) * uvar / chir))

std_cir_list.append(np.sqrt((n - 1) * uvar / chil))

ax.plot(sample_size_list, std_cil_list)

ax.plot(sample_size_list, std_cir_list)

ax.plot(sample_size_list, [h_pop_std]*len(sample_size_list))

ax.set_xlabel("number of samples")

ax.set_ylabel("STD of height(cm)")

ax.set_title("Confidence Interval of STD")

plt.show()

カイ二乗分布～χ2分布

2020-06-16 / tau / 4件のコメント

概要

独立に標準正規分布に従う確率変数X₁, …, X_kがあるとき、以下の統計量は自由度kのカイ二乗分布に従う。

(1) $\begin{equation*} Z = \sum_{i=1}^k {X_i}^2 \end{equation*}$

確率密度関数

x ≥ 0に対して、以下の形をとる。Γはガンマ関数。

(2) $\begin{equation*} f(x; k) = \frac{1}{2^{\frac{k}{2}} \Gamma \left(\dfrac{k}{2} \right)} x^{\frac{k}{2} - 1} e^{-\frac{x}{2}} \end{equation*}$

自由度kのカイ二乗分布の平均はk、分散は2k。

自由度と確率分布の関係

自由度kを変化させたときのカイ二乗分布の確率密度は以下の通り。

χ²分布表

カイ二乗分布は左右非対称なため、左側と右側それぞれの確率値に対するzの値を得る必要がある。以下の計算は、scipy.stats.chi2.ppf()の計算に準拠して、最上段の確率以下となるzの値を示している。

	0.005	0.01	0.025	0.05	0.1	0.9	0.95	0.975	0.99	0.995
5	0.412	0.554	0.831	1.145	1.610	9.236	11.070	12.833	15.086	16.750
6	0.676	0.872	1.237	1.635	2.204	10.645	12.592	14.449	16.812	18.548
7	0.989	1.239	1.690	2.167	2.833	12.017	14.067	16.013	18.475	20.278
8	1.344	1.646	2.180	2.733	3.490	13.362	15.507	17.535	20.090	21.955
9	1.735	2.088	2.700	3.325	4.168	14.684	16.919	19.023	21.666	23.589
10	2.156	2.558	3.247	3.940	4.865	15.987	18.307	20.483	23.209	25.188
11	2.603	3.053	3.816	4.575	5.578	17.275	19.675	21.920	24.725	26.757
12	3.074	3.571	4.404	5.226	6.304	18.549	21.026	23.337	26.217	28.300
13	3.565	4.107	5.009	5.892	7.042	19.812	22.362	24.736	27.688	29.819
14	4.075	4.660	5.629	6.571	7.790	21.064	23.685	26.119	29.141	31.319
15	4.601	5.229	6.262	7.261	8.547	22.307	24.996	27.488	30.578	32.801
16	5.142	5.812	6.908	7.962	9.312	23.542	26.296	28.845	32.000	34.267
17	5.697	6.408	7.564	8.672	10.085	24.769	27.587	30.191	33.409	35.718
18	6.265	7.015	8.231	9.390	10.865	25.989	28.869	31.526	34.805	37.156
19	6.844	7.633	8.907	10.117	11.651	27.204	30.144	32.852	36.191	38.582
20	7.434	8.260	9.591	10.851	12.443	28.412	31.410	34.170	37.566	39.997
30	13.787	14.953	16.791	18.493	20.599	40.256	43.773	46.979	50.892	53.672
40	20.707	22.164	24.433	26.509	29.051	51.805	55.758	59.342	63.691	66.766
50	27.991	29.707	32.357	34.764	37.689	63.167	67.505	71.420	76.154	79.490
60	35.534	37.485	40.482	43.188	46.459	74.397	79.082	83.298	88.379	91.952
70	43.275	45.442	48.758	51.739	55.329	85.527	90.531	95.023	100.425	104.215
80	51.172	53.540	57.153	60.391	64.278	96.578	101.879	106.629	112.329	116.321
90	59.196	61.754	65.647	69.126	73.291	107.565	113.145	118.136	124.116	128.299
100	67.328	70.065	74.222	77.929	82.358	118.498	124.342	129.561	135.807	140.169

なお、これらの値はPythonのscipy.stats.chi2を用いて計算した。

import numpy as np
import scipy.stats as stats

probs = np.array([0.005, 0.01, 0.025, 0.05, 0.1, 0.9, 0.95, 0.975, 0.99, 0.995])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}" \
                   "{1[5]:>7}{1[6]:>7}{1[7]:>7}{1[8]:>7}{1[9]:>7}"
fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}" \
                 "{1[5]:7.3f}{1[6]:7.3f}{1[7]:7.3f}{1[8]:7.3f}{1[9]:7.3f}"

print(fmt_header.format(" ", probs))
for df in range(5, 21):
    print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))
for df in range(30, 101, 10):
    print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

import numpy as np

import scipy.stats as stats

probs = np.array([0.005, 0.01, 0.025, 0.05, 0.1, 0.9, 0.95, 0.975, 0.99, 0.995])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}" \

"{1[5]:>7}{1[6]:>7}{1[7]:>7}{1[8]:>7}{1[9]:>7}"

fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}" \

"{1[5]:7.3f}{1[6]:7.3f}{1[7]:7.3f}{1[8]:7.3f}{1[9]:7.3f}"

print(fmt_header.format(" ", probs))

for df in range(5, 21):

print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

for df in range(30, 101, 10):

print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

母平均の信頼区間～母分散が未知の場合

2020-06-14 / tau / コメントする

概要

母集団の分散がわからない場合の、母平均の信頼区間の推定について。

サンプルの平均値、不偏分散、母平均から計算されるt値がt分布に従うことを利用している。信頼区間の推定の考え方は以下の通り。

サンプルを抽出し、標本平均 $\overline{x}$ と不偏分散s²を求める
サンプルの各データを標本平均と不偏分散で標準化したt値は、サンプル数をnとすると、自由度n−1のt分布に従う
t分布の自由度n−1、信頼確率αに対する値を用いて信頼区間を設定
母平均の信頼区間を計算

手順

まず、母集団からn個のサンプルx₁, …, x_nを抽出し、その平均と不偏分散を求める。

(1) $\begin{align*} \overline{x}_n &= \frac{1}{n}\sum_{i=1}^n x_i \\ {s^2}_n &= \frac{1}{n - 1}\sum_{i=1}^n \left( x_i - \overline{x} \right) \end{align*}$

次に、これらの値から以下のt値を構成する。

(2) $\begin{equation*} t = \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \end{equation*}$

このt値が自由度n−1のt分布に従うことから、意図する確率値αに対する信頼区間を設定。両側に境界を持つ信頼区間の場合は以下のようになる。

(3) $\begin{equation*} t\left( p \le \frac{1 - \alpha}{2}; n-1 \right) \le \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \le t\left( p \le \frac{1 + \alpha}{2}; n-1 \right) \end{equation*}$

これを移項して、平均μに対する信頼区間として表示。

(4) $\begin{equation*} \overline{X}_n - t_{n-1}^{\frac{1-\alpha}{2}} \sqrt{\frac{{s^2}_n}{n}} \le \mu \le \overline{X}_n + t_{n-1}^{\frac{1+\alpha}{2}} \sqrt{\frac{{s^2}_n}{n}} \end{equation*}$

tに関する値は、自由度と意図する確率の値から計算され、こちらに例示した。

例題

このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。

180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7

1	180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7

import numpy as np

np.random.seed(1)

pop_mean = 171.2
pop_std = 6
n_sample = 10

x_sample = np.random.normal(pop_mean, pop_std, n_sample)
np.set_printoptions(precision=1)
print(x_sample)
print("mean = {:5.1f}".format(np.mean(x_sample)))
print("u-var= {:5.2f}".format(np.var(x_sample, ddof=1)))

# [180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7]
# mean = 170.6
# u-var= 56.73

import numpy as np

np.random.seed(1)

pop_mean = 171.2

pop_std = 6

n_sample = 10

x_sample = np.random.normal(pop_mean, pop_std, n_sample)

np.set_printoptions(precision=1)

print(x_sample)

print("mean = {:5.1f}".format(np.mean(x_sample)))

print("u-var= {:5.2f}".format(np.var(x_sample, ddof=1)))

# [180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7]

# mean = 170.6

# u-var= 56.73

これらのデータの平均は170.6、不偏分散は56.73。自由度10 − 1 = 9に対する両側確率95%（片側2.5%）のt値はこちらの表から2.262となることから、μの信頼区間は以下のように計算される。

(5) $\begin{gather*} 170.6 - 2.262 \sqrt{\frac{56.73}{10}} \le \mu \le 170.6 + 2.262 \sqrt{\frac{56.73}{10}} \\ 165.2 \le \mu \le 176.0 \end{gather*}$

この結果は、母分散が既知の場合（168.7～172.5）に比べて区間幅が広くなっている。母分散が未知で情報が少ないのでこれは自然な結果で、式でいえば同じ確率に対するt値が標準正規分布のz値より大きいことと、不偏分散が標準偏差より大きくなることからも確認できる。

t分布

2020-06-14 / tau / コメントする

概要

t分布は連続確率分布の1つで、以下のような場合に用いられる。

正規分布する母集団の平均と分散が未知で標本サイズが小さい場合に平均を推定
2つの平均値の差の統計的有意性に対するt検定

サンプルX₁, …, X_nが平均μの正規分布に従うとし、標本平均 $\overline{X}$ と不偏分散s²が以下であるとする。

(1) $\begin{align*} \overline{X}_n &= \frac{1}{n} \sum_{i=1}^n X_i \\ {s^2}_n &= \frac{1}{n - 1} \sum_{i=1}^n \left( X_i - \overline{X} \right) \end{align*}$

ここで以下の変数（t値）を考える。

(2) $\begin{equation*} t = \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \end{equation*}$

このとき、上記のt値は以下の確率分布でν = n − 1としたものに従うことが知られている。

(3) $\begin{equation*} f(t; \nu) = \dfrac{\Gamma \left( \dfrac{\nu + 1}{2}\right) }{\sqrt{\nu \pi} \Gamma \left( {\dfrac{\nu}{2}}\right)} \left( 1 + \dfrac{t^2}{\nu} \right)^{- \dfrac{\nu + 1}{2} \end{equation*}$

この確率分布はstudentのt分布と呼ばれ、Γはガンマ関数。

自由度と確率分布の関係

t分布の自由度νを変化させて確率分布を描いてみる。

自由度20あたりでかなり標準積分布に近くなっていることがわかる。自由度1～20に対して片側確率が10%, 5%, 2.5%, 1%, 0.5%ととなるzの値を計算すると以下のようになる。

t分布表

以下に、自由度1 ～20に対して、いくつかの片側確率に対するt値の表を示す（Pr(t) > α)となるt値）。

自由度が20くらいになるとかなり標準正規分布に近い形になるが、zの値は有効数値2桁目で違ってくる。自由度が700くらいで何とか3桁目まで標準正規分布の値と同じになる。

ν	0.1	0.05	0.025	0.01	0.005
1	3.078	6.314	12.706	31.821	63.657
2	1.886	2.920	4.303	6.965	9.925
3	1.638	2.353	3.182	4.541	5.841
4	1.533	2.132	2.776	3.747	4.604
5	1.476	2.015	2.571	3.365	4.032
6	1.440	1.943	2.447	3.143	3.707
7	1.415	1.895	2.365	2.998	3.499
8	1.397	1.860	2.306	2.896	3.355
9	1.383	1.833	2.262	2.821	3.250
10	1.372	1.812	2.228	2.764	3.169
11	1.363	1.796	2.201	2.718	3.106
12	1.356	1.782	2.179	2.681	3.055
13	1.350	1.771	2.160	2.650	3.012
14	1.345	1.761	2.145	2.624	2.977
15	1.341	1.753	2.131	2.602	2.947
16	1.337	1.746	2.120	2.583	2.921
17	1.333	1.740	2.110	2.567	2.898
18	1.330	1.734	2.101	2.552	2.878
19	1.328	1.729	2.093	2.539	2.861
20	1.325	1.725	2.086	2.528	2.845
N(0, 1)	1.282	1.645	1.960	2.326	2.576

なお、これらの値はPythonのscipy.statsからt分布と正規分布の関数を呼び出して得られる。

import numpy as np
import scipy.stats as stats

probs = np.array([0.1, 0.05, 0.025, 0.01, 0.005])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}"
fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"
fmt_footer = "{0:>2}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

print(fmt_header.format(" ", probs))
for df in range(1, 21):
    print(fmt_data.format(df, -stats.t.ppf(probs, df=df)))
print()
print(fmt_footer.format("N", -stats.norm.ppf(probs, loc=0, scale=1)))

import numpy as np

import scipy.stats as stats

probs = np.array([0.1, 0.05, 0.025, 0.01, 0.005])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}"

fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

fmt_footer = "{0:>2}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

print(fmt_header.format(" ", probs))

for df in range(1, 21):

print(fmt_data.format(df, -stats.t.ppf(probs, df=df)))

print()

print(fmt_footer.format("N", -stats.norm.ppf(probs, loc=0, scale=1)))

母平均の信頼区間～母分散が既知の場合

2020-06-14 / tau / 5件のコメント

概要

母集団の分散がわかっている場合の、母平均の信頼区間の推定について。

信頼区間の推定の考え方は以下の通り。

サンプルを抽出し、標本平均 $\overline{x}$ を求める
既知の分散σ²から標本平均は正規分布N(μ, σ²/n)に従う
標本平均をμ, σ²/nで標準化し、標準正規分布の信頼確率αに対する信頼区間を設定
母平均μの信頼区間を計算

手順

まず、母集団からn個のサンプルx₁, …, x_nを抽出し、その平均を求める。

(1) $\begin{equation*} \overline{x} = \frac{1}{n}\sum_{i=1}^n x_i \end{equation*}$

次に平均と分散で標準化した変数に対して、意図する確率値αに対する標準正規分布の確率変数値zを使って信頼区間を設定。両側の境界を持つ信頼区間の場合は以下のようになる。

(2) $\begin{equation*} z\left( p \le \frac{1 - \alpha}{2} \right) \le \frac{\overline{x} - \mu}{\sqrt{\sigma^2 / n}} \le z\left( p \le \frac{1+ \alpha}{2} \right) \end{equation*}$

これを移項してμの信頼区間として表示。

(3) $\begin{align*} \overline{x} - z\left( p \le \frac{1 - \alpha}{2} \right) \sqrt{\frac{\sigma^2}{n}} \le \mu \le \overline{x} + z\left( p \le \frac{1+ \alpha}{2} \right) \sqrt{\frac{\sigma^2}{n}} \end{align*}$

信頼確率αに対応する標準正規分布のzを設定してμの信頼区間を算出する。たとえば両側95%信頼区間なら、片側2.5%確率に対応する1.96など、標準正規分布のzの値はこちらを参照。

(4) $\begin{align*} \overline{x} - 1.96 \sqrt{\frac{\sigma^2}{n}} \le \mu \le \overline{x} + 1.96 \sqrt{\frac{\sigma^2}{n}} \end{align*}$

例題

このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。

180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7

1	180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7

これらのデータの平均は170.6となり、これとσ²= 36、サンプル数10、両側95%に対する1.96を用いて、信頼区間は以下のように計算される。

(5) $\begin{gather*} 170.6 - 1.96 \sqrt{\frac{36}{10}} \le \mu \le 170.6 + 1.96 \sqrt{\frac{36}{10}} \\ 166.9 \le \mu \le 174.3 \end{gather*}$

【注】上記のデータはPythonでseed(1)として発生させた。

import numpy as np

np.random.seed(1)

pop_mean = 171.2
pop_std = 6
n_sample = 10

x_sample = np.random.normal(pop_mean, pop_std, n_sample)
np.set_printoptions(precision=1)
print(x_sample)
print("mean = {:5.1f}".format(np.mean(x_sample)))

# [180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7]
# mean = 170.6

import numpy as np

np.random.seed(1)

pop_mean = 171.2

pop_std = 6

n_sample = 10

x_sample = np.random.normal(pop_mean, pop_std, n_sample)

np.set_printoptions(precision=1)

print(x_sample)

print("mean = {:5.1f}".format(np.mean(x_sample)))

# [180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7]

# mean = 170.6

当初seed(0)で発生させた際には以下のようになり、95%信頼区間が母集団の平均を含まなくなった。

[181.8 173.6 177.1 184.6 182.4 165.3 176.9 170.3 170.6 173.7]
mean = 175.6

1 2	[181.8 173.6 177.1 184.6 182.4 165.3 176.9 170.3 170.6 173.7] mean = 175.6

(6) $\begin{gather*} 175.6 - 1.96 \sqrt{\frac{36}{10}} \le \mu \le 175.6 + 1.96 \sqrt{\frac{36}{10}} \\ 171.9 \le \mu \le 179.3 \end{gather*}$

seed(0)はよく使う系列だが、このようなこともあるので乱数系列を複数変えて試すのが望ましい。

サンプルサイズに対する信頼区間の傾向

サンプルサイズを大きくしていったときの平均身長の95%信頼区間は以下の通りで、かなりばらつきながら徐々に区間幅は小さくなるが、ある程度サンプルサイズを大きくしてもあまり顕著な区間幅の減少はみられない。

これは信頼区間に現れる $1/\sqrt{n}$ のグラフを描いてみると分かるが、n=20程度まで急激に小さくなり、その後の減少スピードはかなり遅いことがわかる。したがって、信頼区間を狭めようとしても、効果があるのはせいぜいデータ数50程度までということになる。

【補足】

本記事にいただいたコメントの通り、これの考え方は適切ではない。正しくは、 $1.96 \sqrt{\sigma^2 / 2}$ などのグラフを描くべき。ご指摘に感謝します。

なお、1つ目のグラフの計算手順は以下の通り。

母集団の平均・標準偏差から、サンプルサイズを変えながら正規乱数を発生させる
サンプルごとにサンプル平均を計算する
サンプル平均と母分散から母平均推定の信頼区間の上限値と下限値を計算してリストに追加する
結果をグラフに表示する

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt

rnd.seed(0)

# height of Japanese in 2017(40-49, #374)
hpop_mean = 171.2
hpop_std = 6.0
hpop_var = hpop_std ** 2

sample_size_list = range(10, 200)
z95 = 1.96

fig, ax = plt.subplots()

hsmp_mean_conf_lower95 = []
hsmp_mean_conf_upper95 = []
for nsmp in sample_size_list:
    hsmp = rnd.normal(loc=hpop_mean, scale=hpop_std, size=nsmp)
    hsmp_mean = np.mean(hsmp)
    hsmp_mean_conf_lower95.append(hsmp_mean - z95 * np.sqrt(hpop_var / nsmp))
    hsmp_mean_conf_upper95.append(hsmp_mean + z95 * np.sqrt(hpop_var / nsmp))

ax.plot(sample_size_list, hsmp_mean_conf_upper95,
    linestyle='solid', label="CI(95%)-Upper")
ax.plot(sample_size_list, hsmp_mean_conf_lower95,
    linestyle='dashed', label="CI(95%)-Lower")
ax.plot(sample_size_list, [hpop_mean]*len(sample_size_list),
    linestyle='dashdot', label="Pop mean")

ax.set_xlabel("sample size")
ax.set_ylabel("height(cm)")
ax.set_title("Confidence Interval of Height(40-49)")
ax.legend()

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

rnd.seed(0)

# height of Japanese in 2017(40-49, #374)

hpop_mean = 171.2

hpop_std = 6.0

hpop_var = hpop_std ** 2

sample_size_list = range(10, 200)

z95 = 1.96

fig, ax = plt.subplots()

hsmp_mean_conf_lower95 = []

hsmp_mean_conf_upper95 = []

for nsmp in sample_size_list:

hsmp = rnd.normal(loc=hpop_mean, scale=hpop_std, size=nsmp)

hsmp_mean = np.mean(hsmp)

hsmp_mean_conf_lower95.append(hsmp_mean - z95 * np.sqrt(hpop_var / nsmp))

hsmp_mean_conf_upper95.append(hsmp_mean + z95 * np.sqrt(hpop_var / nsmp))

ax.plot(sample_size_list, hsmp_mean_conf_upper95,

linestyle='solid', label="CI(95%)-Upper")

ax.plot(sample_size_list, hsmp_mean_conf_lower95,

linestyle='dashed', label="CI(95%)-Lower")

ax.plot(sample_size_list, [hpop_mean]*len(sample_size_list),

linestyle='dashdot', label="Pop mean")

ax.set_xlabel("sample size")

ax.set_ylabel("height(cm)")

ax.set_title("Confidence Interval of Height(40-49)")

ax.legend()

plt.show()

Logistic回帰～1変数・Excelによる解

2020-04-04 / tau / コメントする

例題のデータ

ある旅行会社の会員顧客20人の年齢と、温泉(SPA)とレジャーランド(LSR)のどちらを選んだかというデータが以下のように得られているとき、新たな顧客にどちらを勧めればより適切か。

このようなクラス分けの問題にLogistic回帰を使うのにPythonのパッケージなどによる方法もあるが、ここではExcelを使った方法を示す。

その流れは、各観光客の選択結果のカテゴリー変数と年齢から個別の尤度と合計の尤度の計算式を定義し、切片と係数の初期値を設定しておいてから、尤度が最大となるような切片・係数を求めるためにExcelのソルバーを使う。

元となるデータは、各観光客の年齢と、行先に選んだのが温泉(SPA)かレジャーランドか(LSR)の別、それらに対して温泉を選んだ場合は1、レジャーランドを選んだ場合は0となるカテゴリー変数。

計算表の準備

このデータから以下のような表を作る。各セルの意味と内容は以下の通り。

coef：線形式の切片Aと係数Bの初期値としてそれぞれ0をセットし、収束計算の結果が入る
intercept：切片の計算のために使われるデータで、全て固定値の1
prob：coefがA, Bの値の時に各顧客の年齢に対してis_spa=1となる確率で、Logistic関数の計算値
- セルの内容は計算式で=1/(1+EXP(-$A*Y-$B*Z))
- $A, $Bは固定座標を表し、全てのデータに対してこれらのセルの内容を使う
LH：is_spaの値に対する尤度(likelihood)
- セルの内容は計算式でX*LN(C)+(1-X)*LN(1-C)
MLE：全データのLHの和で、このデータセットのパターンに対する最大尤度の結果が入る

収束計算

データタブの一番右にあるソルバーに入る(ない場合はファイル→オプション→アドイン→設定からソルバーアドインにチェックを入れる)。

ソルバーのパラメーター設定ダイアログで、

目的セルを上記のDで選択
変数セルを上記のA:Bの範囲で選択。
目標値は「最大値」を選択

「解決」ボタンを押して収束計算すると、Dの値を最大化するA:Bの内容がセットされる。

この場合の結果は以下の通り

coef：-13.6562, 0.234647
MLE：-7.45298

確率0.5(線形式の値が0)を温泉とレジャーランドの閾値とするなら、それに相当する年齢は以下のように計算される。

(1) $\begin{equation*} -13.6562 + 0.234647 \times x = 0 \quad \rightarrow \quad x = \frac{13.6562 }{0.234647 } =58.2 \end{equation*}$

Pythonのscikit-learnのLogisticRegressionモデルを同じデータに適用した結果(C=1e5)は以下の通りで、かなり近い値となっている。

intercept_ = [-13.38993211]
coefficient_ = [0.23015561]

得られた係数の値を使って、以下の関数式のグラフを描いてみたのが以下の図でLogistic曲線が現れている。

二項分布

2020-03-01 / tau / コメントする

概要

ある試行において起こり得る事象が2通りしかない場合、このような試行をベルヌーイ試行(Bernoulli trial)という。たとえばコインを投げた時に表が出るか裏が出るか、くじ引きを引いたときに当たりが出るかはずれが出るか、など。

ベルヌーイ試行の2つの事象を確率変数 $X = 1, 0$ で表し、 $X = 1$ となる確率が $p$ であるとする。

(1) $\begin{alignat*}{1} P(X=1) &= p \\ P(X=0) &= 1-p \end{alignat*}$

このようなベルヌーイ試行を $n$ 回繰り返したとき、 $X=1$ が生じる回数の確率分布が二項分布(Binomial distribution)で、 $B(n, p)$ のように表示される。二項分布の例には以下のようなものがある。

コインの表／裏が出る確率が等しく1/2のとき、このコインを10回投げた時に表がでる回数の分布
打率3割の打者が4回打席に立って2安打以上打つ確率

確率分布

$n$ 回のベルヌーイ試行のうち、 $X=1$ が $k$ 回起こるケースは、 ${}_n \mathrm{C}_k$ 通りなので、二項分布の確率は以下のように表せる。

(2) $\begin{equation*} P(X=k ; p) = {}_n \mathrm{C}_k p^k (1-p)^{n-k} \end{equation*}$

全事象

$k=0~n$ の確率の和が全事象の確率であり、二項定理から、

(3) $\begin{equation*} \sum_{k=0}^n {}_n \mathrm{C}_k p^k (1-p)^{n-k} = (p + 1 - p)^n = 1 \end{equation*}$

平均と分散

二項分布 $B(n, p)$ の平均と分散は、以下のようになる。

(4) $\begin{alignat*}{1} E(X) &= np \\ V(X) &= np(1-p) \end{alignat*}$

この導出において興味深いテクニックが使われる。

二項分布の形

$n=20, p=0.3$ の二項分布のグラフをPythonで描くと以下のようになる。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

n = 20
p = 0.3

min_k = 0
max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)
binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")
ax.hist(data, bins=20, range=(min_k, max_k), density=True,
    color='c', edgecolor='k', label="binomial trials")
ax.legend(loc="upper right")
ax.text(15, 0.175, "n={}".format(n))
ax.text(15, 0.165, "p={}".format(p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

n = 20

p = 0.3

min_k = 0

max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)

binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()

ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")

ax.hist(data, bins=20, range=(min_k, max_k), density=True,

color='c', edgecolor='k', label="binomial trials")

ax.legend(loc="upper right")

ax.text(15, 0.175, "n={}".format(n))

ax.text(15, 0.165, "p={}".format(p))

plt.show()

正規分布近似

二項分布 $B(n, p)$ は、 $np, np(1-p)$ が十分大きいとき(具体的には5より大きいとき)、平均 $np$ 、分散 $np(1-p)$ の正規分布で近似できる(ド・モアブル－ラプラスの定理)。

(5) $\begin{equation*} X \sim B(n, p) \rightarrow \frac{X - np}{\sqrt{np(1-p)}} \sim N=(0, 1) \end{equation*}$

これは、二項分布の1回の試行において成功する場合をX_i = 1、失敗する場合をX_i = 0として、成功回数 $\sum X_i$ の平均と分散がnp, np(1 − p)であることからわかる。

以下は、 $n, p$ の3つずつの組み合わせに対する、二項分布と正規分布の一致具合を比べたもの。表示範囲は、正規分布とみなしたときの $-3\sigma \sim 3\sigma$ に対応する範囲で設定している。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))
fig.subplots_adjust(hspace=0.3)

n_subplot = 0
for n in [10, 100, 1000]:
    for p in [0.15, 0.3, 0.5]:
        n_subplot += 1
        k = np.arange(0, n + 1)
        mu = n * p
        sig = np.sqrt(n * p * (1 - p))
        binom_pmf = binom.pmf(k, n, p)
        norm_pdf = norm.pdf(k, loc=mu, scale=sig)

        ax = fig.add_subplot(3, 3, n_subplot)
        ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))
        ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")
        ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")
        ax.legend(loc="lower center", fontsize=8)
        ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))

fig.subplots_adjust(hspace=0.3)

n_subplot = 0

for n in [10, 100, 1000]:

for p in [0.15, 0.3, 0.5]:

n_subplot += 1

k = np.arange(0, n + 1)

mu = n * p

sig = np.sqrt(n * p * (1 - p))

binom_pmf = binom.pmf(k, n, p)

norm_pdf = norm.pdf(k, loc=mu, scale=sig)

ax = fig.add_subplot(3, 3, n_subplot)

ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))

ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")

ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")

ax.legend(loc="lower center", fontsize=8)

ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

母集団確率の最尤推定

二項分布の母集団確率の最尤推定量は $p=k/n$ である。

実用例

適用例

二項確率が与えられたときの、発生回数や個体数の予測。

当たりの確率がpの掛けの、掛け回数nと当たりの回数k
故障率pの部品について、n個の部品のうちの故障数k
罹患率pの病気について、n人のうちの罹患者数k
支持率pの政党に対して、n人のうちの支持者数k

分析例

上記と逆に、nサンプルから事象がk回発生したときの確率を推定。

概要

基本のデータ

定義

医学・疫学上の指標

陽性率／陰性率

的中率

有病率／陽性率など

補足：感度と特異度について

補足：「特異度」という表現について

ここで定義する記号

条件付確率による表示

感度／特異度（真陽性率／真陰性率）

偽陽性率／偽陰性率

陽性的中率／陰性的中率

実際の使われ方

概要

ブートストラップ法による信頼区間の推定

概要

手順

例題

サンプルサイズに対する信頼区間の傾向

概要

自由度と確率分布の関係

χ2分布表

概要

手順

例題

概要

自由度と確率分布の関係

t分布表

概要

手順

例題

サンプルサイズに対する信頼区間の傾向

例題のデータ

計算表の準備

収束計算

概要

確率分布

全事象

平均と分散

二項分布の形

正規分布近似

母集団確率の最尤推定

実用例

適用例

分析例

χ²分布表