離散的な方法による確認
単位時間あたりの到着率![]() のポアソン過程において、時刻0に到着が発生した後、次の到着があるまでの時間間隔が
のポアソン過程において、時刻0に到着が発生した後、次の到着があるまでの時間間隔が![]() 以下である確率を考える。
以下である確率を考える。
![]() を
を![]() 等分し、
等分し、![]() とすると、到着間隔が
とすると、到着間隔が![]() 以下なので、連続して到着しなかった後に到着が発生する事象を重ね合わせて、以下のように表せる。
以下なので、連続して到着しなかった後に到着が発生する事象を重ね合わせて、以下のように表せる。
(1) 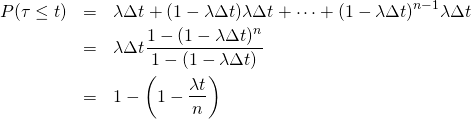
ここで![]() とおいて
とおいて![]() の極限をとると、
の極限をとると、
(2) ![]()
となって指数分布の確率分布関数を得る。
確率密度関数を直接求める方法
到着時間間隔の確率密度関数を![]() とし、
とし、![]() の間は到着が発生せず、
の間は到着が発生せず、![]() で到着が発生する場合を考える。
で到着が発生する場合を考える。
(3) ![]()
これより、
(4) ![]()
両辺を![]() で微分して、
で微分して、
(5) ![]()
この微分方程式の解は、
(6) ![]()
確率密度関数なので、全定義域の積分値が1となることから、
(7) ![]()
これより![]() を得るので、確率密度関数は以下のように得られる。
を得るので、確率密度関数は以下のように得られる。
(8) ![]()
Poisson分布から導く方法
ポアソン過程に関して、以下のPoisson分布を考える。
(9) ![]()
ここで、時刻![]() の間に全く到着がない確率はその時間の間
の間に全く到着がない確率はその時間の間![]() であるから、
であるから、
(10) ![]()
ここで、到着時間間隔が![]() 以下である確率は、
以下である確率は、![]() の間に1回以上到着がある事象の和であり、「1回も到着がない」事象の余事象でもある。これより、以下の指数分布の分布関数を得る。
の間に1回以上到着がある事象の和であり、「1回も到着がない」事象の余事象でもある。これより、以下の指数分布の分布関数を得る。
(11) ![]()