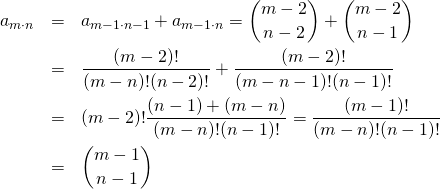二項定理の表現
(1) 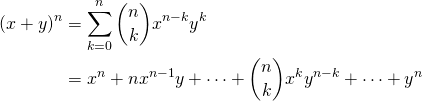
具体例
(2) 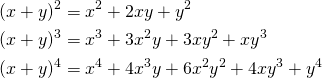
証明
数学的帰納法で証明する。
![]() のとき、
のとき、
(3) ![]()
![]() のとき、
のとき、
(4) ![]()
ここで![]() のときに以下が成り立つとする。
のときに以下が成り立つとする。
(5) 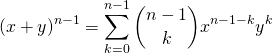
このとき![]() に関しては、
に関しては、
(6) 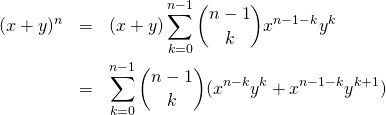
これを右辺は以下のように展開できる。
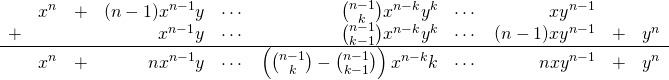
(7) 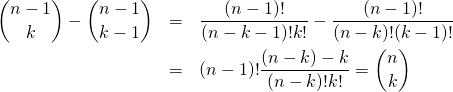
これより、![]() に対して(1)が証明された。
に対して(1)が証明された。
パスカルの三角形
数のような数による三角形をパスカルの三角形(Pascal’s triangle)と呼び、n行目の数の列が二項展開のn乗の係数となっている。
各項の計算の仕方は、一つ上の段の左右の数の和として求めていく(左端・右端の外側はゼロと考える)。

パスカルの三角形の各項が二項展開の計数となること、すなわちm段目のn項目の数を![]() とし、これが
とし、これが![]() となることを、数学的帰納法で証明する。
となることを、数学的帰納法で証明する。
(8) 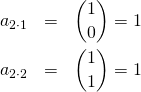
(9)