基本
ロシアンルーレットは、賭の順番問題や条件付き確率の問題としてよく見かける。まず、一番基本的なルールで考える。
n回目に実弾に当たる確率を![]() とすると、
とすると、
1発目で当たる確率は、6つの弾倉のどこかに実弾が入っているので、
(1) ![]()
2発目で当たる確率は、1発目で実弾に当たらず、2発目は残り5つの弾倉のどこかに実弾が入っているので、
(2) ![]()
以下、6発目まで同じように考えて、
(3) 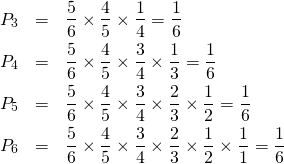
すなわち、通常のロシアンルーレットでは、1~6回目のどこで実弾に当たる確率も等しく1/6で、順番の後先に有利性はない。
毎回シリンダーを回転させる場合
毎回シリンダーを回転させるので、そこまで発砲されていなければ、実弾である確率は毎回1/6。![]() 回目に実弾に当たる確率を
回目に実弾に当たる確率を![]() とすると、
とすると、![]() 回は当たらないことを考慮して、
回は当たらないことを考慮して、
(4) ![]()
まず、この確率はnが大きくなるほどゼロに近づく。たとえば1回めで当たる確率は約16.7%、10回目で当たる確率は約3.2%、20回目で当たる確率は0.5%、40回目だと約0.01%程度となる。
次に、![]() 回目までに当たる確率を
回目までに当たる確率を![]() とすると、これは各回の確率を累積していくことで求められるので、等比数列の和より、
とすると、これは各回の確率を累積していくことで求められるので、等比数列の和より、
(5) 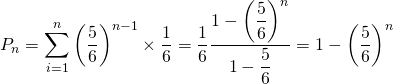
この累積確率は![]() のとき1に近づくが、10回目で約83.8%、20回目で約97.4%、30回目で約99.6%、40回目で約99.9%となり、100回も打ってその時点で生き延びている確率はほとんどゼロに近い。
のとき1に近づくが、10回目で約83.8%、20回目で約97.4%、30回目で約99.6%、40回目で約99.9%となり、100回も打ってその時点で生き延びている確率はほとんどゼロに近い。
次に交互に打っていく場合を考える。
先攻で打つ方になった場合、1回目、3回目・・・と奇数回に打つことになるので、その累積確率を![]() とすると、
とすると、
(6) 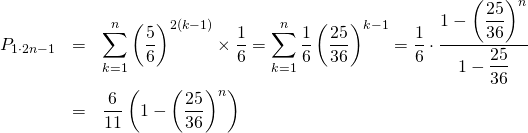
後攻で打つ方になった場合は、2回目、4回目・・・と偶数回に打つことになるので、その累積確率を![]() とすると、
とすると、
(7) 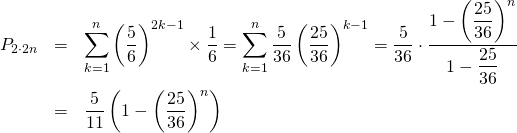
同じ![]() に対して常に
に対して常に![]() となり、先に打つのを選んだほうが実弾に当たる確率は高く、この比率は
となり、先に打つのを選んだほうが実弾に当たる確率は高く、この比率は![]() としたときの結果と同じ。
としたときの結果と同じ。
したがって、「お先にどうぞ」と相手に最初を譲ったほうが、少しでも生き残る確率が高くなる。また、3人以上で順番に打っていく場合は、できるだけ後の順番で打つ方が実弾に当たる確率が低くなる。
条件付きの問題
2発の弾を並べて込める
ロシアンルーレットと少し違うが、条件付きの問題。
1発目が空砲の場合
まず、シリンダーをもう一度回転させてから打つ場合は、6弾倉中2発残っているので、当たる確率は1/3。逆に助かる率は2/3となる。
一方シリンダーを回転させない場合は、手渡された拳銃の弾の状態を、円形に並んだ弾倉を一列で表し、下表のように整理する。ただし、左欄の●は実弾がある場所、○は実弾が入っていない場所で、1番目は金貸しが打ったときの位置、2番目は手渡された時の位置。右欄は2発目が実弾の場合は●、空砲の場合は○とする。
| ●●○○○○ | 対象外 |
| ○●●○○○ | ● |
| ○○●●○○ | ○ |
| ○○○●●○ | ○ |
| ○○○○●● | ○ |
| ●○○○○● | 対象外 |
金貸しが打ったときは空砲だったので、1番目が実弾の事象は対象外。このとき、実弾に当たらない確率は3/4となる。
すなわち、もう一度シリンダーを回転させるよりも、そのまま続けて打った方が助かる可能性が高い。
1発目が実弾の場合
この場合に続けて打つと、1発目が実弾である2ケースに対して、空砲で助かる率は1/2。
シリンダーを回転させてから打つと、実弾は残り1発なので、当たらない確率は5/6で、回転させて打った方が生存確率は高くなる。
条件に応じた選択と確率
以上の結果を整理すると下表の通りとなり、1発目が空砲の場合と実弾の場合で、その後の選択による生存確率の高い方が逆転している。
空砲も実弾もその位置が連続しているため、1発目が空砲の場合は続けて空砲の確率が高く、1発目が実弾の場合は次も実弾の確率が高そうだが、1発目が実弾の場合は弾が1つ消費されるので、その影響で結果が逆転している。
| 1発目 | 選択 | 生存確率 |
| 空砲 | シリンダー回転 | 1/3 (0.33) |
| 空砲 | 続けて打つ | 3/4 (0.75) |
| 実弾 | シリンダー回転 | 5/6 (0.83) |
| 実弾 | 続けて打つ | 1/2 (0.50) |
実弾2発をランダムに込める
上記の金貸しの問題では実弾2発を並べて込めたが、これをランダムな位置に2発込めた場合はどうなるか。
この場合、2発の実弾の装填状況は下表のようになる。
| 1発目が→ | 空砲 | 実弾 |
| ●●○○○○ | 対象外 | ● |
| ●○●○○○ | 対象外 | ○ |
| ○●●○○○ | ● | 対象外 |
| ●○○●○○ | 対象外 | ○ |
| ○●○●○○ | ● | 対象外 |
| ○○●●○○ | ○ | 対象外 |
| ●○○○●○ | 対象外 | ○ |
| ○●○○●○ | ● | 対象外 |
| ○○●○●○ | ○ | 対象外 |
| ○○○●●○ | ○ | 対象外 |
| ●○○○○● | 対象外 | ○ |
| ○●○○○● | ● | 対象外 |
| ○○●○○● | ○ | 対象外 |
| ○○○●○● | ○ | 対象外 |
| ○○○○●● | ○ | 対象外 |
1発目が空砲だった場合
シリンダーを回転させた場合の生存確率は、4/6 = 2/3 (0.667)。
続けて打つ場合は、1発目が実弾のケースを除いて2発目が空砲の場合なので、6/10 = 3/5 (0.6)。
1発目が実弾だった場合
シリンダーを回転させた場合の生存確率は、5/6 (0.833)。
続けて打つ場合は、1発目が空砲のケースを除いて2発目が空砲の場合なので、4/5 (0.8)。
1発目が空砲でも実弾でも、シリンダーを回転させた方が生き残る確率が高くなる。