相関係数の定義
相関係数は、多数のデータの組がどの程度線形に近い性質を持つかを表す値で、以下で定義される。
(1) ![Rendered by QuickLaTeX.com \begin{eqnarray*} r &=& \frac{{\rm Cov}(X, Y)}{\sqrt{V(X) \cdot V(Y)}} \\ &=& \frac{E(X - \overline{X})(Y - \overline{Y})} {\sqrt{ ( E\left[ (X - \overline{X})^2 \right] E\left[ (Y - \overline{Y})^2 \right] }} \\ &=& \frac{\displaystyle \sum_{i=1}^{n}(x_i - \overline{x})(y_i - \overline{y})} {\left[ \displaystyle \sum_{i=1}^{n} (x_i - \overline{x})^2 \displaystyle \sum_{i=1}^{n} (y_i - \overline{y})^2 \right]^{1/2}} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-b9969ab54d441dc3797aad03fd503747_l3.png)
相関係数の線形変換
変数を線形変換した場合の相関係数は分散・共分散の性質から、以下のようになり、元のままか符号が反転する。
(2) 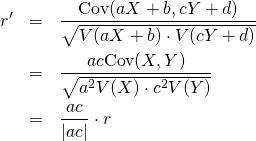
完全線形関係の場合の相関係数
XとYが完全な線形関係にある場合、相関係数は1または-1になる。このとき、傾きの大きさや、平行移動は相関係数に影響しない。
(3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} r &=& \frac{ {\rm Cov}(X, aX+b) } { \left[ V(X) \cdot V(aX+b) \right]^{1/2} } \\ &=& \frac{ a {\rm Cov}(X, X) } { \left[ V(X) \cdot a^2 V(X) \right]^{1/2} } \\ &=& \frac{a}{\sqrt{a^2}} \cdot \frac{ {\rm Cov}(X, X) } { \left[ V(X) \cdot V(X) \right]^{1/2} } \\ &=& \frac{a}{|a|} \cdot \frac{ V(X) } { V(X) } \\ &=& 1 \; {\rm or} \; -1 \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-0d7ce9a0442d3932b94aab482cf5e5d2_l3.png)
いろいろな分布の相関係数
完全な線形関係
以下のコードで確認。
相関係数は傾きや平行移動に対して影響を受けず、増加関数なら1、減少関数なら-1になることがわかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import numpy as np import numpy.random as rnd import matplotlib.pyplot as plt def cor(x, y): return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std() x = np.linspace(0.2, 0.8, num=21) y01 = np.array([x for x in x]) y02 = np.array([x * 0.5 for x in x]) y03 = np.array([x + 0.2 for x in x]) y04 = np.array([1 - x for x in x]) plt.axes().set_aspect('equal') plt.xlim(0, 1) plt.ylim(0, 1) plt.scatter(x, y01, label='cor=' + str(cor(x, y01))) plt.scatter(x, y02, label='cor=' + str(cor(x, y02))) plt.scatter(x, y03, label='cor=' + str(cor(x, y03))) plt.scatter(x, y04, label='cor=' + str(cor(x, y04))) plt.legend() plt.show() |
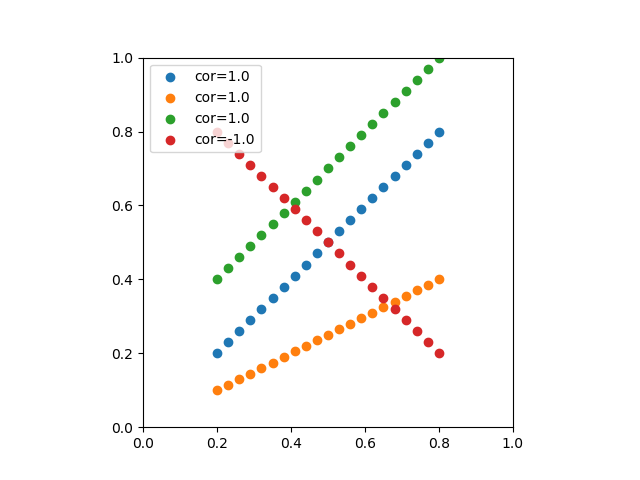
線形性が強い関係
線形関数の値に対して、乱数でばらつきを与えた場合の相関係数の違いを示す。ばらつきが大きい方が相関係数は小さくなる。
|
1 2 3 |
y11 = np.array([x for x in x]) y12 = np.array([x + rnd.rand() * 0.2 * rnd.choice([-1, 1]) for x in x]) y13 = np.array([x + rnd.rand() * 0.4 * rnd.choice([-1, 1]) for x in x]) |
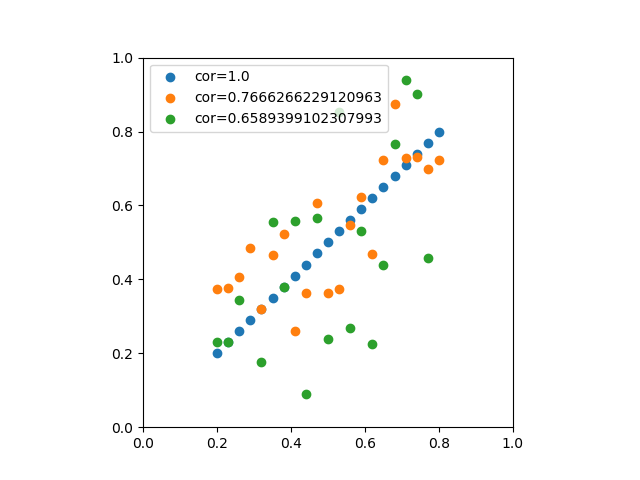
負の線形性が強い場合は、相関係数がマイナスになる。
|
1 2 3 |
y21 = np.array([1 - x for x in x]) y22 = np.array([1 - x + rnd.rand()*0.2*rnd.choice([-1, 1]) for x in x]) y23 = np.array([1 - x + rnd.rand()*0.4*rnd.choice([-1, 1]) for x in x]) |
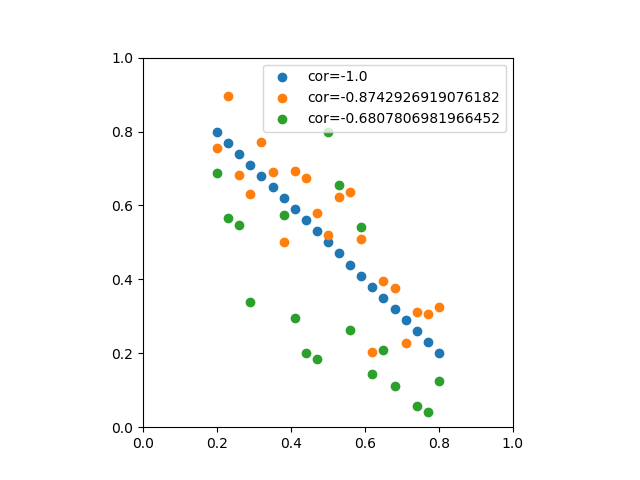
放物線(強い関係があるのに相関が低いケース)
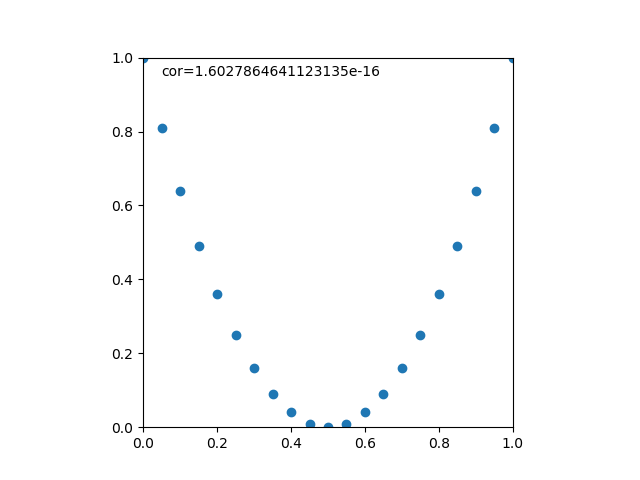
以下のような放物線では、XとYにきちんとした数学的関係があるのに、相関係数がゼロに近くなる。
相関係数はXとYが単調増加/単調減少の度合いが強いほど、また線形関係に近いほど1に近くなるが、それ以外の関係が強い場合にはそれを補足できない場合がある。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np import numpy.random as rnd import matplotlib.pyplot as plt def cor(x, y): return np.sum((x - x.mean())*(y - y.mean())) / len(x) / x.std() / y.std() x = np.linspace(0, 1.0, num=21) y1 = np.array([4 * (x - 0.5)**2 for x in x]) plt.axes().set_aspect('equal') plt.xlim(0, 1) plt.ylim(0, 1) plt.scatter(x, y1) plt.text(0.05, 0.95, 'cor=' + str(cor(x, y1))) plt.show() |
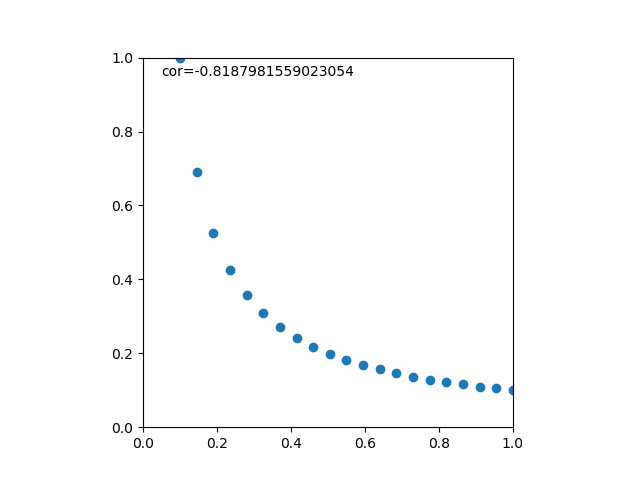
反比例(負の線形性に見えてしまう場合)
以下は反比例関数の場合。
関数の形状や範囲に寄るが、この場合は相関係数の絶対値が0.8以上と1に近く、これだけ見ると負の線形性が強そうに見える。
|
1 2 |
x = np.linspace(0.1, 1.0, num=21) y2 = np.array([0.1 / x for x in x]) |
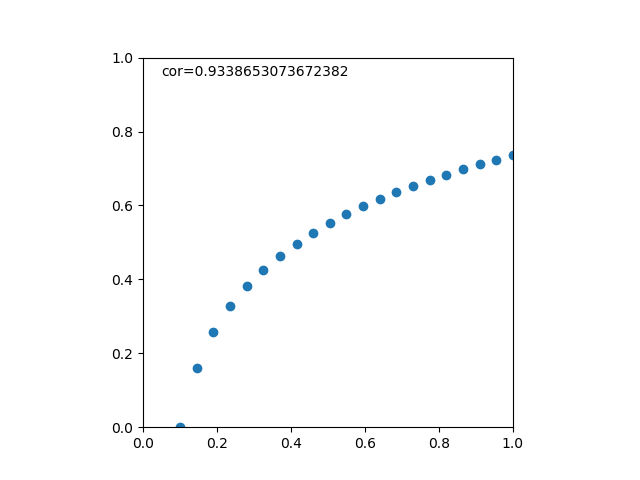
対数関数(正の線形性に見えてしまう場合)
対数関数の場合。この場合は0.9以上とかなり強い線形性を示唆している。
|
1 2 |
x = np.linspace(0.1, 1.0, num=21) y3 = np.array([np.log(x*20-1)/4 for x in x]) |
相関係数に関する注意
本来の関係との乖離
先にみたように、線形関係ではないが数学的な関係を持つ場合に、相関係数からは全く関係がない、元の関係とは異なり線形関係を持つ、といった解釈になることがある。
相関係数が高い場合に、線形回帰式などで物事を予測する際には注意が必要。
変数間に解析的な関係が見いだせるならそれを重視すべきであり、よしんばそれがわからないにしても、定義域の範囲で「ある程度は当たる」程度に考えておくべきか。
因果関係
堂々と間違えられるケースが、「科学的な」記事やマスメディアなどでよくみられる。
相関係数は「変数間の単調な増加/減少傾向が強いかどうか」だけを示すもので、必ずしも因果関係を示唆しない。
気温が高いとビールはよく売れるがおでんは売れない。その二つに負の相関があるからといって、「ビール好きはおでんが嫌い」と言えないが、形を変えてこのような解釈がなされる恐れがある。
もともとのメカニズムで因果関係が示唆されていて、その上で相関係数の大きさを論じるなら意義もあるが、その場合でも、事象に対する寄与度などをよく考えておかないと「それだけが原因」と考えるような間違いを犯すことになる。