導入
以下のように行列表示された連立方程式を考える。
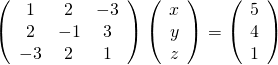
この方程式の解は、![]() 。
。
逆行列による方法
係数行列、未知数ベクトル、定数ベクトルをそれぞれ![]() と表す。
と表す。
![]()
このとき係数行列に逆行列が存在するなら、未知数ベクトルは以下で解ける。
![]()
これをnumpy.linalgパッケージの行列操作で解いてみる。
行列にベクトルを掛けるのに、reshape()で行ベクトルから列ベクトルに変換している点に注意。
|
1 2 3 4 5 6 7 8 9 10 |
A = np.array([[1, 2, -3], [2, -1, 3], [-3, 2, 1]]) b = np.array([5, 4, 1]) print(LA.inv(A) @ b.reshape(3, 1)) # [[2.] # [3.] # [1.]] |
numpy.linalg.solve()による方法
solve(A, b)関数は、第1引数に係数行列、第2引数に定数ベクトルを与えて、連立方程式の解のベクトルを得ることができる。
|
1 2 3 4 5 6 7 8 |
A = np.array([[1, 2, -3], [2, -1, 3], [-3, 2, 1]]) b = np.array([5, 4, 1]) print(LA.solve(A, b)) # [2. 3. 1.] |
非正則行列の場合
以下のような、明らかな非正則行列の場合(連立方程式が不定の場合)、逆行列を計算しようとする時点でsingular matrixのエラーになる。
|
1 2 3 4 5 |
A = np.array([[1, 1], [2, 2]]) b = np.array([2, 4]) print(LA.inv(A)) # numpy.linalg.LinAlgError: Singular matrix |
このようなケースでは、linalg.solve()関数でも同様のエラーとなる。
|
1 2 3 4 5 |
A = np.array([[1, 1], [2, 2]]) b = np.array([2, 4]) print(LA.solve(A, b)) # numpy.linalg.LinAlgError: Singular matrix |
以下のようなケースはややこしい。同じ係数行列と定数ベクトルに対して、逆行列による解とsolve()による解の値が異なっている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) b = np.array([1, 2, 3]) print(LA.det(A)) print(LA.inv(A) @ b.reshape(3, 1)) print(LA.solve(A, b)) # 6.66133814775094e-16 # [[ 2.] # [-4.] # [ 0.]] # [-0.33333333 0.66666667 0. ] |
行列Aの行列式は理論上はゼロであることが確認できる。
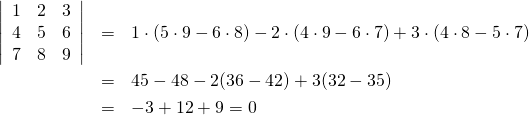
この方程式を掃き出し法で解いていくと以下の通り。
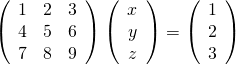
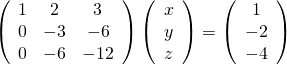
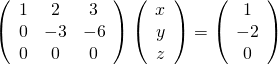
途中省略するが、ここでzを消去すると、![]() となり、先の計算結果と符合するが、zは0である必要はない。
となり、先の計算結果と符合するが、zは0である必要はない。
不定連立方程式において、逆行列やsolve()関数を使って解く場合には注意が必要。