公式
Cauchy-Schwaltz inequality
(1) 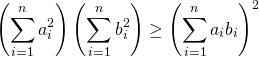
証明
n=2の場合
(2) ![]()
(3) 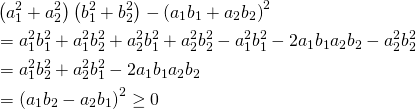
nが任意の場合
2次方程式の判別式による方法
以下の2次方程式を考える。
(4) 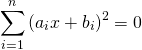
ここで関数![]() であり、上記の2次方程式の数は0個または1個である。
であり、上記の2次方程式の数は0個または1個である。
この方程式は以下のように変形できる。
(5) ![]()
もとの方程式の解の個数が0 or 1なので、上記の方程式の判別式から
(6) 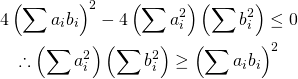
イメージ
![]() 、
、![]() とすると、ベクトルの内積となす角の関係から
とすると、ベクトルの内積となす角の関係から
(7) ![]()